


Next: Rendering Primitives
Up: Introduction
Previous: A Short History
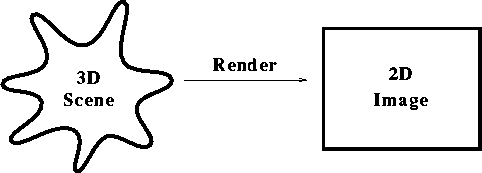
- Rendering is the conversion of a scene
into an image:
 \
\
- The scene composed of models
in three space.
Models, composed of
primitives, supported
by the rendering system.
- Models entered by hand or created by a program.
For our purposes today, models already generated.
- The image drawn on monitor,
printed on laser printer, or
written to a raster in memory or a file.
These different
possibities require us to consider device independence.
- Classically, ``model'' to ``scene'' to ``image''
conversion broken into finer
steps, called the graphics pipeline.
Commonly implemented in graphics hardware to get interactive speeds.
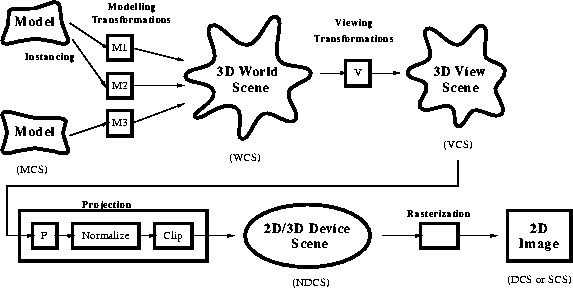
- At a high level, the graphics pipeline usually looks like
 \
\
- Each stage refines the scene,
converting primitives in modelling space
to primitives in device space,
where they are converted to pixels (rasterized).
- A number of coordinate systems are used:
- MCS:
- Modelling Coordinate System.
- WCS:
- World Coordinate System.
- VCS:
- Viewer Coordinate System.
- NDCS:
- Normalized Device Coordinate System.
- DCS or SCS:
- Device Coordinate System or
equivalently the Screen Coordinate System.
Keeping these straight is the key to
understanding a rendering system.
- Transformation between two coordinate systems
represented with matrix.
- Derived information may be added (lighting and shading)
and primitives may be removed
(hidden surface removal) or modified (clipping).
 Readings: Hearn and Baker, Section 6-1 (but they give a more
detailed version than used here).
Red book, 6-1, 6-6 (intro).
White book, 8-3,
Blinn: 16.
Readings: Hearn and Baker, Section 6-1 (but they give a more
detailed version than used here).
Red book, 6-1, 6-6 (intro).
White book, 8-3,
Blinn: 16.
We begin with a description of forward rendering, which
is the kind of rendering usually supported in hardware and is the model
OpenGL uses. In forward rendering, rendering primitives are
transformed, usually in a conceptual pipeline, from the model to the device.
However, raytracing, which we will consider later in the
course, is a form of backward rendering. In backward
rendering, we start with a point in the image and work out what
model primitives project to it.
Both approaches have advantages and disadvantages.



Next: Rendering Primitives
Up: Introduction
Previous: A Short History
CS488/688: Introduction to Interactive Computer Graphics
University of Waterloo
Computer Graphics Lab
cs488@cgl.uwaterloo.ca
 \
\
 \
\