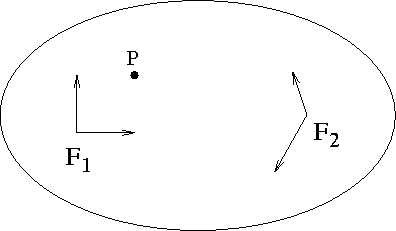
- We have two coordinate frames for a space,
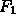 and
and 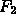 ,
,
- Want to change from coordinates relative
to
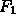 to coordinates relative to
to coordinates relative to 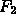 .
.
- Express each component of
 in terms of
in terms of  :
:

- The change of coordinates is given by the matrix

Factoring gives
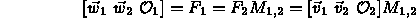
- Consider:

- If
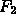 is orthonormal:
is orthonormal:

- If
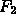 is orthogonal:
is orthogonal:

- Otherwise, we have to solve a small system of
linear equations, using
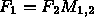 .
.
- Change of basis from
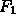 to Standard Cartesian Frame
is trivial
(since frame elements normally expressed with respect
to Standard Cartesian Frame).
to Standard Cartesian Frame
is trivial
(since frame elements normally expressed with respect
to Standard Cartesian Frame).
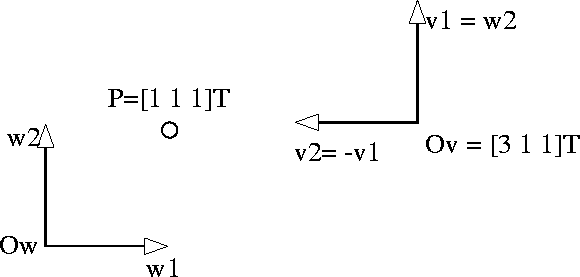 \
\
where ![]() is the standard coordinate frame.
is the standard coordinate frame.
- Matrices mapping from/to
 to/from
to/from  :
:
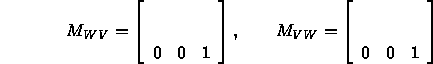
- Check
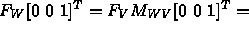
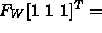
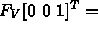
- Define two frames:
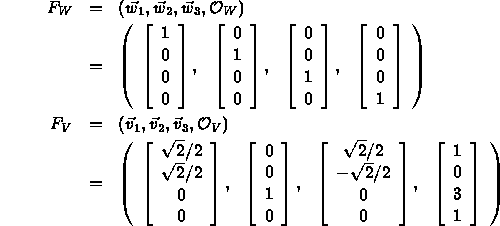
- All coordinates are specified relative to the standard frame in a Cartesian 3 space.
- The standard frame happens to be identical to
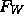 .
.
- Note that both
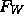 and
and 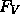 are orthonormal.
are orthonormal.
- The matrix mapping
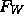 to
to 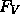 is given by
is given by
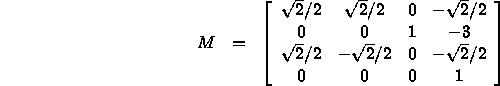
- Check this matrix:
Map each element of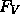 ,
,
See that we get that element relative to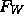 .
.
(e.g,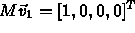 )
)
- Question: What is the matrix mapping from
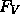 to
to 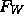 ?
?
- On the computer, frame elements usually
specified in Standard Frame for space.
Eg, a frame
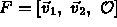 is given by
is given by
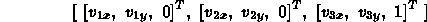
relative to Standard Frame.
Question: What are coordinates of these basis elements relative to F?
- Frames are usually orthonormal.
- A point ``mapped'' by a change of basis
does not change;
We have merely expressed its coordinates relative to a different frame.