Geometric Transformations

Construct

matrices for simple geometric transformations.

Combine

simple transformations into more complex ones.

• Assume that the range and domain frames are the Standard Frame.
• Will begin with 2D, generalize later.

Translation:

Specified by the vector :

• A point 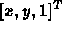will map to .
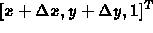• A vector will remain unchanged under translation.
• Translation is NOT a linear transformation.
  If it were, then (ignoring the fact that point addition is not allowed) T(P+Q)=T(P)+T(Q) would hold, BUT: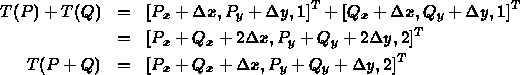

  

• Translation is linear on sums of vectors...

Matrix representation of translation

• We can create a matrix representation of translation:

  

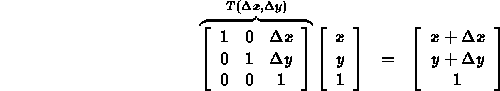
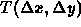• will mean the above matrix.
• Note that vectors are unchanged by this matrix.
• Although more expensive to compute than the other version of translation, we prefer this one:
  • Uniform treatment of points and vectors
  • Other transformations will also be in matrix form.
    We can compose transformations by matrix multiply. Thus, the composite operation less expensive if translation composed, too.

Scale about the origin:

 
Specified by factors .

• Applies to points or vectors, is linear.
• A point 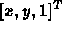will map to .
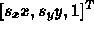• A vector 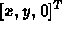will map to .
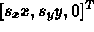• Matrix representation:

  

Rotation:

Counterclockwise about the origin, by angle .

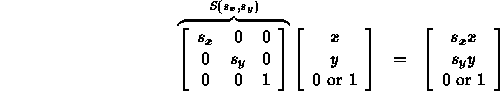
• Applies to points or vectors, is linear.
• Matrix representation:

  

Shear:

Intermixes coordinates according to :

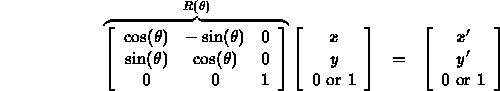
• Applies to points or vectors, is linear.
• Matrix representation:

  

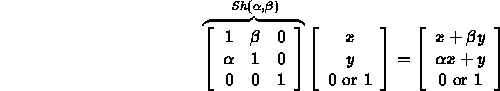
• Easiest to see if we set one of 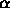or 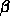to zero.

Reflection:

Through a line.

• Applies to points or vectors, is linear.
• Example: through x-axis, matrix representation is

  

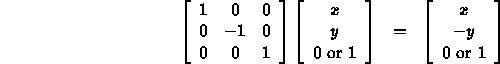
• See book for other examples

Note:

Vectors map through all these transformations as we want them to.

Readings: Hearn and Baker, 5-1, 5-2, and 5-4; Red book, 5.2, 5.3; White book, 5.1, 5.2