- Metric d(P,Q) must satisfy the following axioms:
-
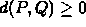
- d(P,Q) = 0 iff P = Q.
- d(P,Q) = d(Q,P).
-
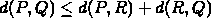 .
.
-
- Distance is intrinsic to the space, and not a property of the frame.
![]()
- Dot product is defined on vectors.
- Distance metric is defined on points.
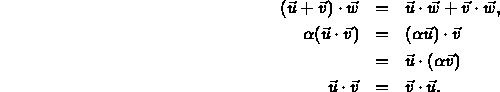
![]()
![]()
![]()
Perpendicularity is not an affine concept!