- How do we model for a Ray Tracer?
- Hierarchical modeling works well, but we can do more easily.
- In Constructive Solid Geometry all primitives are solids.
- New type of internal node: Boolean operation.
Intersection, Union, Difference
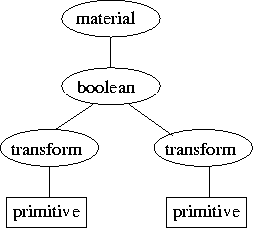
- Thus, our model is a DAG with
- Leaf nodes representing primitives
- Interal nodes are transformations, materials, or boolean operations.
 \
\
We will want a rich set of primitives. How do we specify them?
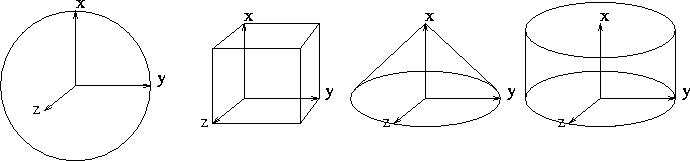
- As a ``canonical'' primitive
 \
\
Sphere()*Scale(2,2,2)*Translate(x,y,z)
- As a transformed canonical primitive
- Sphere(r,x,y,z);
- Cube(x,y,z,dx,dy,dz);
- Cone(width,height,x,y,z,dx,dy,dz);
- After transformation are applied, our primitives will be warped.
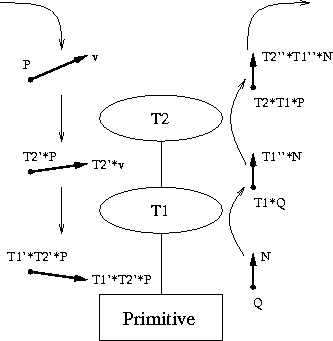
- Rather than intersect ray with warped primitive (which is worse once we add boolean operations), we will transform the ray.
- On the way down, apply inverse transformation to ray.
- On the way back, apply the transformation to the point
and to the normal
Caution: see notes on transforming normals
 \
\
Note: In this figure, T' is used to denote
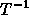 ,
T'' denotes
,
T'' denotes 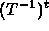
- Could apply boolean operations to transformed primitives
and construct a surface for that object.
Problem: representation too complex
- Idea: perform a complete ray intersect object with each
primitive. This gives us a (set of) line segment(s).
Next, perform boolean operations on line segments.
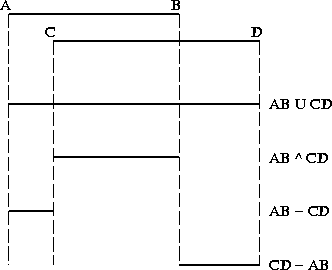 \
\
- Note that if we transform the ray on the way down, then we must transform the entire segment on the way back
- Also, we must be careful with normals: they flip when we perform difference.