- Illumination models require:
- surface normal vectors at intersection points
- ray-surface intersection computation must also yield a normal
- light-source directions must be established at intersection
- shadow information determined by light-ray intersections with other objects
- Normals to polygons:
- provided by planar normal
- provided by cross product of adjacent edges
- Or use phong normal interpolation if normals specified at vertices
- Normals to any implicit surface (eg. quadrics)
- move from (x,y,z) to
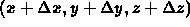 which is maximally far from the surface
which is maximally far from the surface
- direction of greatest increase to f(x,y,z)
- move from (x,y,z) to
- Taylor series:
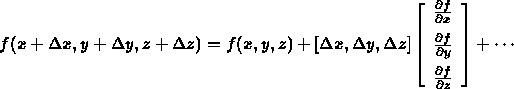
- maximality for the gradient vector of f
- not normalized
- Normal to a quadric surface
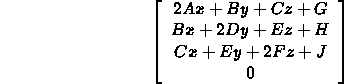
- Let
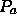 and
and 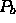 be any two points on object
be any two points on object
- arbitrarily close
-
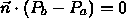
- using transpose notation:

- After an affine transformation on
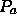 ,
, 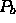 :
:

we want
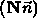 to be a normal for some
transformation N:
to be a normal for some
transformation N:

and this certainly holds if
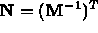
- Only the upper 3-by-3 portion of M is pertinent for vectors
- Translation:
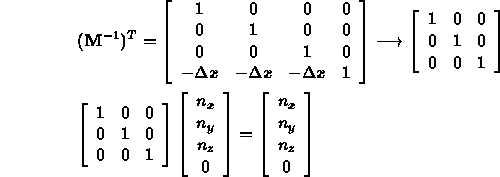
 no change to the normal
no change to the normal
- Rotation (example):
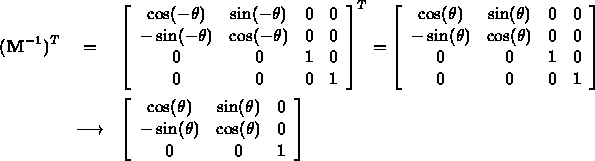
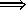 rotation applied unchanged to normal
rotation applied unchanged to normal
- Scale:
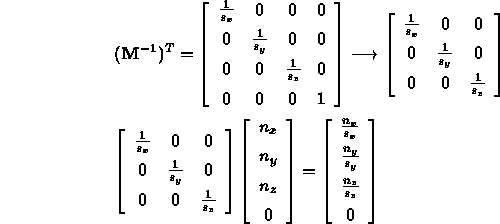
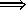 reciprocal scale applied to normal
reciprocal scale applied to normal