Transforming Normals

The Truth:

Can really only apply affine transforms to points.
Vectors can be transformed correctly iff they are defined by differences of points.

Transforming Normal Vectors:

• Normal vectors ARE NOT defined by differences of points.
• Tangent vectors ARE defined by differences of points.
• Normals are vectors perpendicular to all tangents at a point:

  

• Note that the natural representation of 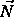is as a row vector.
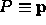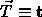• Suppose we have a transformation M, a point , and a tangent at P.
• Let 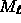be the ``linear part'' of M, i.e. the upper 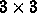submatrix.

  

• Transform normals by inverse transpose of linear part of transformation: .
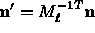• If 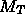is O.N. (usual case for rigid body transforms), .

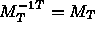Only worry if you have a non-uniform scale or a shear transformation.

Transforming lines:

Transform implicit form in a similar way.

Transforming planes:

Transform implicit form in a similar way.

Readings: Red Book, 5.8 (?); White Book, 5.6.