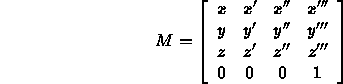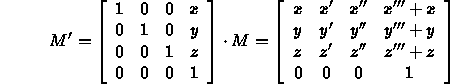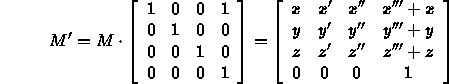World and Viewing Frames

• Typically, our space S is a Cartesian space.
  • Call the standard frame the world frame.
  • The world frame is typically right handed.
  • Our scene description is specified in terms of the world frame.
• The viewer may be anywhere and looking in any direction.
  • Often, x to the right, y up, and z straight ahead.
    • z is called the viewing direction.
    • Note that this is a left handed coordinate system.
  • We could instead specify z and y as vectors
    • z is the the view direction.
    • y is the up vector.
    • Compute
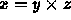
    • Get a right handed coordinate system.
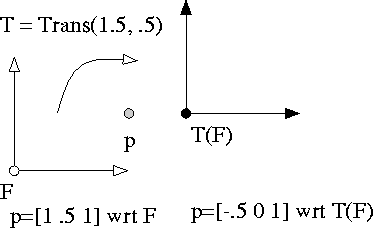
  • We can do a change of basis
    • Specify a frame relative to the viewer.
    • Change coordinates to this frame.
• Once in viewing coordinates,
  • Usually place a clipping ``box'' around the scene.
  • Box oriented relative to the viewing frame.
• An orthographic projection is made by ``removing the z-coordinate.''
  • Squashes 3D onto 2D, where we can do the window-to-viewport map.
  • The projection of the clipping box is used as the window.
• Mathematically, relative to

  

  we map onto

  

  as follows:

  

  or if we ignore the frames,

  

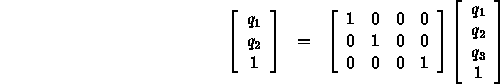
• We can write this in matrix form:

  

Viewing-World-Modeling Transformations

: 

• Want to do modeling transformations and viewing transformation (as in Assignment 2).
• If V represents World-View transformation, and M represents modeling transformation, then

  

  transforms from modeling coordinates to viewing coordinates.

  Note: M is performing both modeling transformation and Model to World change of basis.

• Question: If we transform the viewing frame (relative to viewing frame) how do we adjust V?
• Question: If we transform model (relative to modeling frame) how do we adjust M?

Viewing Transformations:

 

• Assume all frames are orthonormal
• When we transform the View Frame by T, apply to anything expressed in old view frame coordinates to get new View Frame coordinates

  \

• To compute new World-to-View change of basis, need to express World Frame in new View Frame

  Get this by transforming World Frame elements represented in old View Frame by .

• Recall that the columns of the World-to-View change-of-basis matrix are the basis elements of the World Frame expressed relative to the View Frame.
• If V is old World-to-View change-of-basis matrix, then will be new World-to-View change-of-basis matrix, since each column of V represents World Frame element, and the corresponding column of contains of this element.

Modeling Transformations:

 

• Note that the columns of M are the Model Frame elements expressed relative to the World Frame.
• Want to perform modeling transformation relative to modeling coordinates.
• If we have previously transformed Model Frame, then we next transformation relative to transformed Model Frame.
• Example: If

  

  and we translate one unit relative to the first Model Frame basis vector, then we want to translate by (x,y,z,0) relative to the World Frame.

• Could write this as

  

• But this is also equal to

  

• In general, if we want to transform by T our model relative to the current Model Frame, then

  

  yields that transformation.

• Translation is easy to do either way, but rotations are much easier the latter way, since rotations around Model Frame basis vectors.
• Summary:

  Modeling transformations embodied in matrix M

  World-to-View change of basis in matrix V

  VM transforms from modeling coordinates to viewing coordinates

  If we further transform the View Frame by T relative to the View Frame, then the new change-of-basis matrix V' is given by

  

  If we further transform the model by T relative to the modeling frame, the new modeling transformation M' is given by

  

• For Assignment 2, need to do further disection of transformations, but this is the basic idea.

Readings: Hearn and Baker, Section 6-2, first part of Section 12-3; Red book, 6.7; White book, 6.6