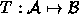Ambiguity

3 Types of Transformations:

1. (between two spaces)
2. (``warp'' an object within its own space)
3. T: change of coordinates

Changes of Coordinates:

• Given 2 frames:
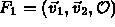  • , orthonormal,
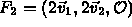  • , orthogonal.
• Suppose .
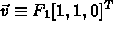• Then .

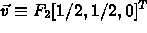Question:

What is the length of ?

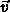Answer:

Its length is       , regardless of its frame of representation.

Suppose

we have and

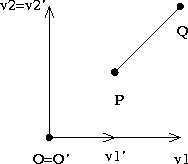
• P,Q relative to ,
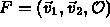• We are given a matrix representation of a transformation T:

  

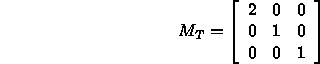
• Consider P'=TP and Q'=TQ.
• How do we interpret P' and Q'?
  1. Change of Coordinates?

     \

  2. Scale?

  3. Transformations between spaces?

• With no other information, any of the above is a valid interpretation.

Do we care?

YES!

• In (1) nothing changes except the representation.
• In (1) distances are preserved while they change in (2) and the question has no meaning in (3).
• In (3), we've completely changed spaces.

Consider

the meaning of |P'-P|

1. |P'-P|=0
2. 
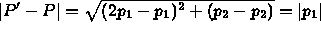
3. |P'-P| has no meaning

We need

1. A matrix
2. A domain space
3. A range space
4. A coordinate frame in each space

to fully specify a transformation.

Most of the time not all will be specified!

...So be careful out there.