


Next: Affine Space
Up: Geometries
Previous: Geometries
- Definition:
-
- Axioms:
-
- Addition Commutes:
-
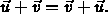
- Addition Associates:
-

- Scalar Multiplication Distributes:
-

- Unique Zero Element:
-

- Field Unit Element:
-

- Span:
-
- Suppose
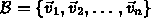 .
.
-
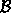 spans
spans 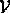 iff
any
iff
any 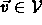 can be written as
can be written as  .
.
- This is written
 .
.
-
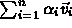 is a
linear combination of the vectors in
is a
linear combination of the vectors in 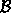 .
.
- Basis:
-
- Any minimal spanning set is a basis.
- All bases are the same size.
- Dimension:
-
- The number of vectors in any basis.
- We will work in 2 and 3 dimensional spaces.
- Note:
- In the definition of a Vector Space:
- No notion of distance or size
- No notion of angles
- No ``points''
These are Euclidean and Affine space concepts.
CS488/688: Introduction to Interactive Computer Graphics
University of Waterloo
Computer Graphics Lab
cs488@cgl.uwaterloo.ca
 .
.
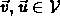 :
:
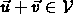 .
.
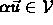 , where
, where 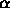 is
a member of some field
is
a member of some field 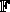 ,
(i.e.
,
(i.e. 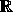 ).
).
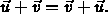




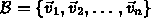 .
.
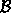 spans
spans 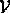 iff
any
iff
any 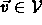 can be written as
can be written as  .
.
 .
.
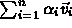 is a
linear combination of the vectors in
is a
linear combination of the vectors in 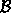 .
.