Point and Line Clipping

Clipping:

Remove points outside a region of interest.

• Discard (parts of) primitives outside our window...

Point clipping:

Remove points outside window.

• A point is either entirely inside the region or not.

Line clipping:

Remove portion of line segment outside window.

• Line segments can straddle the region boundary.
• Liang-Barsky algorithm efficiently clips line segments to a halfspace.
• Halfspaces can be combined to bound a convex region.
• Use outcodes to better organize combinations of halfspaces.
• Can use some of the ideas in Liang-Barsky to clip points.

Parametric representation of line:

or equivalently

• A and B are non-coincident points.
• For 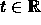, L(t) defines an infinite line.
• For 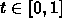, L(t) defines a line segment from A to B.
• Good for generating points on a line.
• Not so good for testing if a given point is on a line.

Implicit representation of line:

• P is a point on the line.
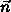• is a vector perpendicular to the line.
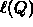• gives us the signed distance from any point Q to the line.
• The sign of 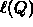tells us if Q is on the left or right of the line, relative to the direction of .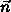
• If 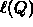is zero, then Q is on the line.
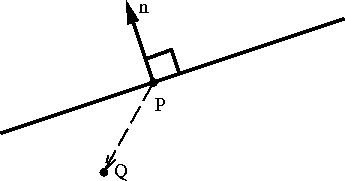
• Use same form for the implicit representation of a halfspace.

\

Clipping a point to a halfspace:

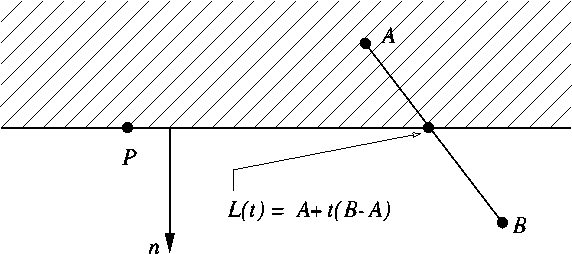
• Represent window edge as implicit line/halfspace.
• Use the implicit form of edge to classify a point Q.
• Must choose a convention for the normal:
  points to the inside.
• Check the sign of :
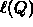  • If 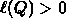, then Q is inside.
  • Otherwise clip (discard) Q:
    It is on the edge or outside.
    May want to keep things on the boundary.

Clipping a line segment to a halfspace:

There are three cases:

1. The line segment is entirely inside:
   Keep it.
2. The line segment is entirely outside:
   Discard it.
3. The line segment is partially inside and partially outside:
   Generate new line to represent part inside.

\

Input Specification:

• Window edge: implicit,
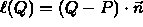
• Line segment: parametric, L(t) = A + t(B-A).

Do the easy stuff first:

We can devise easy (and fast!) tests for the first two cases:

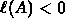• AND 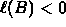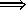Outside
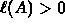• AND 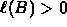Inside

Need to decide: are boundary points inside or outside?

Trivial tests

are important in computer graphics:

• Particularly if the trivial case is the most common one.
• Particularly if we can reuse the computation for the non-trivial case.

Do the hard stuff only if we have to:

If line segment partially inside and partially outside, need to clip it:

• Line segment from A to B in parametric form:

  

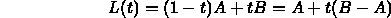
• When t=0, L(t)=A. When t=1, L(t)=B.
• We now have the following:

  \

• We want t such that :

  

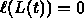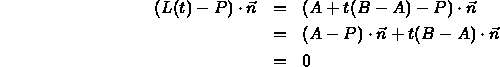
• Solving for t gives us

  

• NOTE:
  The values we use for our simple test can be reused to compute t: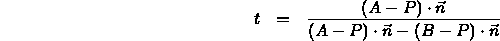

  

Clipping a line segment to a window:

Just clip to each of four halfspaces in turn.

Pseudo-code:

	Given line segment (A,B), clip in-place:
	for each edge (P,n)
	    wecA = (A-P) . n
	    wecB = (B-P) . n
	    if ( wecA < 0 AND wecB < 0 ) then reject
	    if ( wecA > 0 AND wecB > 0 ) then next
	    t = wecA / (wecA - wecB)
	    if ( wecA < 0 ) then 
	        A = A + t*(B-A)
	    else
	        B = A + t*(B-A)
	    endif
	endfor

Note:

• Liang-Barsky Algorithm can clip lines to any convex window.
• Optimizations can be made for the special case of horizontal and vertical window edges.

Question:  
Should we clip before or after window-to-viewport mapping?

Line-clip Algorithm generalizes to 3D:

• Half-space now lies on one side of a plane.
• Plane also given by normal and point.
• Implicit formula for plane in 3D is same as that for line in 2D.
• Parametric formula for line to be clipped is unchanged.

Reading: Hearn and Baker, Sections 6-5 through 6-7, Red book: 3.9, White Book: 3.11, Blinn: 13.