Tensor Product Patches

Tensor Product Patches:

• The control polygon is the polygonal mesh with vertices
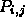
• The patch basis functions are products of curve basis functions

  

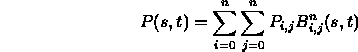
  where

  

Properties:

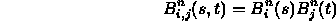
• Patch basis functions sum to one

  

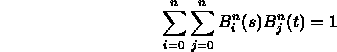
• Patch basis functions are nonnegative on

  

  

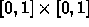
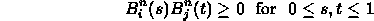
  Surface patch is in the convex hull of the control points
  

  

  Surface patch is affinely invariant
  (Transform the patch by transforming the control points)

Subdivision, Recursion, Evaluation:

• As for curves in each variable separately and independently
• Tangent plane is not produced!
  • Normals must be computed from partial derivatives.

Partial Derivatives:

Ordinary derivative in each variable separately:

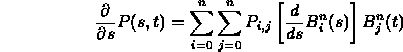
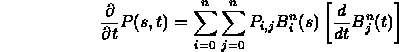
Each of the above is a tangent vector in a parametric direction

Surface is regular at each (s,t) where these two vectors are linearly independent

The (unnormalized) surface normal is given at any regular point by

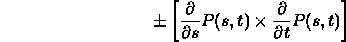
(the sign dictates what is the outward pointing normal)

In particular, the cross-boundary tangent is given by
(e.g. for the s=0 boundary):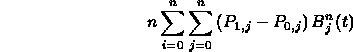

(and similarly for the other boundaries)

Smoothly Joined Patches:

Can be achieved by ensuring that

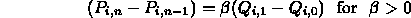
(and correspondingly for the other boundaries)

Rendering:

• Divide up into polygons:

  A.

  By stepping

  

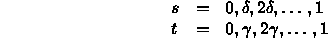
  and joining up sides and diagonals to produce a triangular mesh

  B.

  By subdividing and rendering the control polygon