Bézier Splines

Bezier Curve Segments and their Properties

Definition:

A degree n (order n+1) Bézier curve segment is

where the are k-dimensional control points.

Convex Hull:

, for
P(t) is a convex combination of the for
P(t) lies within convex hull of for .

Affine Invariance:

A Bézier curve is an affine combination of its control points.
Any affine transformation of a curve is the curve of the transformed control points.

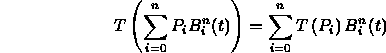
This property does not hold for projective transformations!

Interpolation:

, , , for
if , if
, .

Derivatives:

, .

Smoothly Joined Segments ( ):

Let , be the last two control points of one segment.
Let , be the first two control points of the next segment.

Smoothly Joined Segments ( ):

:
If then segments have same derivatives at endpoints and are said to meet with continuity

Recurrence, Subdivision:

de Casteljau's algorithm:

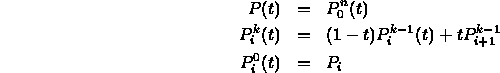
Use to evaluate point at t, or subdivide into two new curves:

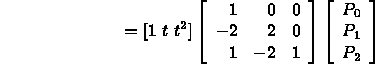
• , , ... are the control points for the left half;
• , , ... are the control points for the right half

Matrix view:

• Expand each Bernstein polynomial in powers of t
• Represent each expansion as the column of a matrix
• Quadratic example:

  

  

• In matrix format:

  

  • is the monomial basis
  • is a matrix containing the coefficients of the polynomials for each dimension of
  • is a change of basis matrix that converts a specification P of P(t) relative to the Bernstein basis to one relative to the monomial basis