- Ray: express in parametric form

where E is the eyepoint and P is the pixel point
- Scene Object: direct implicit form
- express as f(Q)=0 when Q is a surface point, where f is a given formula
- intersection computation is an equation to solve:
find t such that f(E+t(P-E))=0
- Scene Object: procedural implicit form
- f is not a given formula
- f is only defined procedurally
-
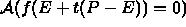 yields t,
where A is a root finding method
yields t,
where A is a root finding method
(secant, Newton, bisection, ...)
- Surface given by
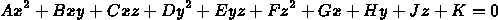
- Ray given by

- Substitute ray x,y,z into surface formula
- quadratic equation results for t
- organize expression terms for numerical accuracy; ie. to avoid
- cancellation
- combinations of numbers with widely different magnitudes
- The plane of the polygon should be known
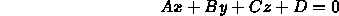
- (A,B,C,0) is the normal vector
- pick three succesive vertices

- should subtend a ``reasonable'' angle
(bounded away from 0 or 180 degrees) - normal vector is the cross product
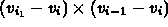
- D = -(Ax+By+Cz) for any vertex (x,y,z,1) of the polygon
- Substitute ray x,y,z into surface formula
- linear equation results for t
- Solution provides planar point
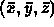
- is this inside or outside the polygon?
- Take origin point and two independent vectors on the plane

- Express any point in the plane as
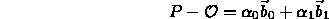
- intersection point is
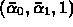
- clipping algorithm against polygon edges
in these
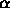 coordinates
coordinates
- intersection point is
- Alternative: Intersections in model space
- form normals and planar coordinates in model space and store with model
- backtransform the ray into model space using inverse modeling transformations
- perform the intersection and illumination calculations
- Alternative: Intersections in world space
- form normals and planar coordinates in model space and store
- forward transform using modeling transformations