


Next: Do's and Don'ts
Up: Polygons
Previous: Polygon Clipping
- Once we have mapped the vertices of polygon to device
coordinates, we want to scan convert it.
- Scan converting a general polygon is complicated.
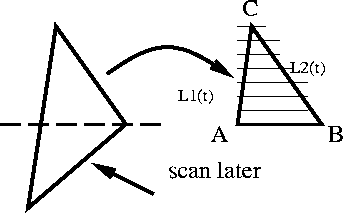
- Here we will look at scan conversion of a triangle.
- Look at y value of vertices. Split triangle along
horizontal line at middle y value.
 \
\
- Step along L1 and L2 together along the scan lines
from A to C and from B to C respectively.
- Scan convert each horizontal line.
- Code for triangle scan conversion
-
 Readings: Hearn and Baker, Chapter 3-11;
Red book, 3.5 (more general than above);
White book, 3.6 (more general than above).
Readings: Hearn and Baker, Chapter 3-11;
Red book, 3.5 (more general than above);
White book, 3.6 (more general than above).
CS488/688: Introduction to Interactive Computer Graphics
University of Waterloo
Computer Graphics Lab
cs488@cgl.uwaterloo.ca
 \
\
 .
.