- Identify all points with a line through the eyepoint.
- Slice lines with viewing plane, take intersection point
as projection.
 \
\
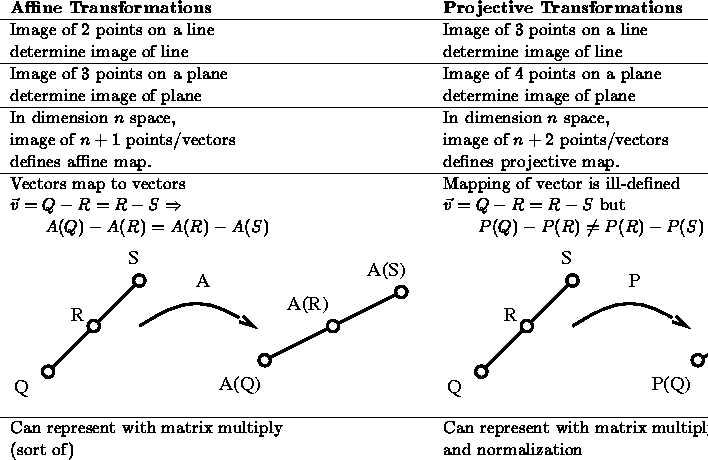
- This is not an affine transformation, but a projective transformation.
- Angles are not preserved (not preserved under Affine Transformation).
- Distances are not preserved (not preserved under Affine Transformation).
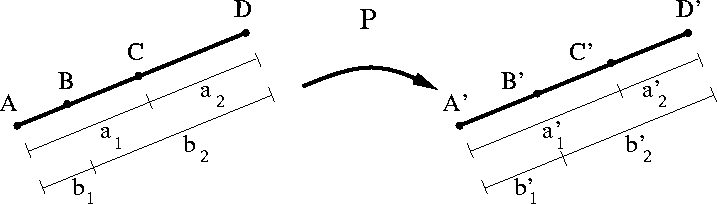
- Ratios of distances are not preserved.
- Affine combinations are not preserved.
- Straight lines are mapped to straight lines.
- Cross ratios are preserved.
- Cross ratio:
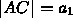 ,
, 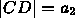 ,
, 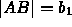 ,
, 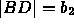 , then
, then

This can also be used to define a projective transformation (ie, that lines map to lines and cross ratios are preserved).
- Given a point S, we want to find its projection P.
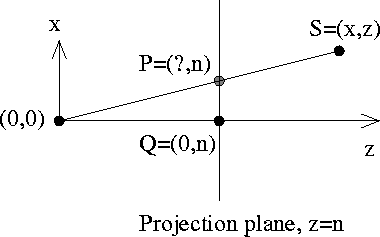 \
\
- Similar triangles: P=(xn/z, n)
- In 3D,
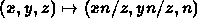
- Have identified all points on a line through the origin with a point in the projection plane.
- Thus,
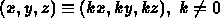 .
.
- These are known as homogeneous coordinates.
- If we have solids or coloured lines,
then we need to know ``which one is in front''. - This map loses all z information, so it is inadequate.
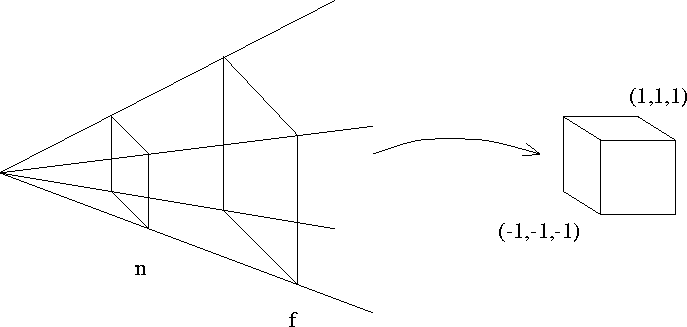
- Maps a near clipping plane z=n to z'= -1
- Maps a far clipping plane z=f to z'=1
 \
\
- The ``box'' in world space known as
``truncated viewing pyramid'' or ``frustum''
- Project x, y as before
- To simplify things, we will project into the z=1 plane.
- Want to map x to x/z (and similarly for y).
- Use a matrix multiply followed by a division (normalization):
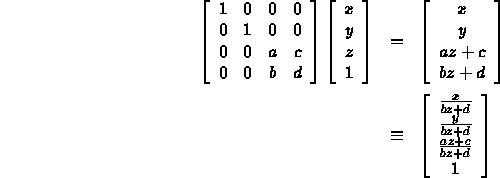
- Solve for a, b, c, and d such that
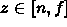 maps to
maps to 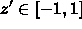 .
.
- Know that we want to map x to x/z (assuming
our projection plane is at z=1) so
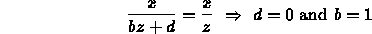
Thus,
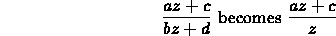
- Our constraints on the near and far clipping planes
(e.g., that they map to -1 and 1) give us
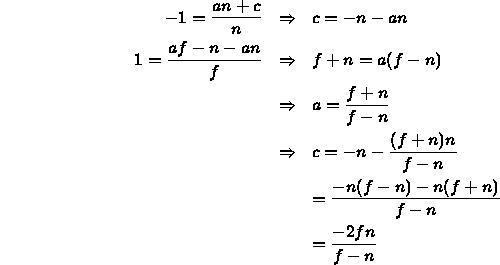
This gives us
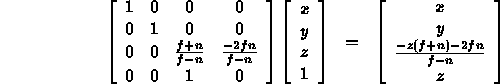
- After normalizing we get

- Could use this formula instead of performing the matrix multiply followed by the division ...
- If we multiply this matrix in with the geometric transforms,
the only additional work is the divide.
- If z=n, then
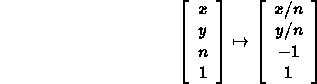
- If z=f, then
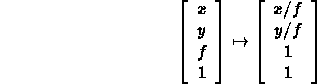
-
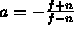 and b=-1.
and b=-1.
- OpenGL looks down z=-1 rather than z=1.
- Note that when you specify n and f,
they are given as positive distances down z=-1.
- The upper left entries are very different.
- OpenGL uses this one matrix to both project and map to NDC.
- How do we set x or y to map to [-1,1]?
- We don't want to do both because we may not have square windows.
- Let's do y:
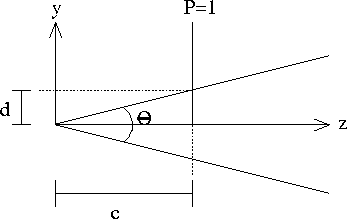 \
\
- Want to map distance d to 1.
-
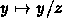 is the current projection ...
is the current projection ...
-
 gives us the scaling.
gives us the scaling.
- But we have placed our
projection plane at z=1, so this is
really

where c=1.
- But
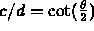 so
so

- Finally, because the x-y aspect ratio
may not be 1, we will scale x to give
the desired ratio:

where aspect
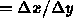 of the
viewport.
of the
viewport.
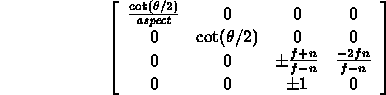
where the ![]() is 1 if we look down the z axis and -1 if
we look down the -z axis.
is 1 if we look down the z axis and -1 if
we look down the -z axis.