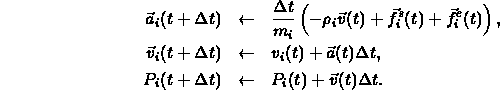Spring-Mass Models

1. Create a model:
   • Composed of a mesh of point masses 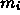connected by springs with spring constants 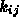and rest lengths .
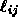   • Let 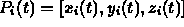be the position of mass 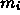at time t.
   • Let 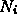be the set of all indices of masses connected to mass .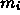

     If 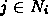, then 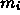and 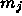are connected by a spring.

   • Springs exert force proportional to displacement from rest length, in a direction that tends to restore the rest length:

     

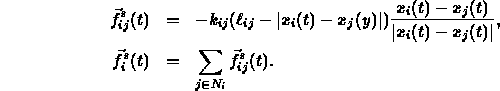
   • Masses assumed embedded in a medium that provides a damping force of

     

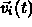     is velocity of 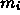at time t.

     (Damping could also be provided on the derivative of the change in rest length of the springs, which would be coordinate-system independent.)

2. Motion of each mass governed by second order ordinary differential equation:

   

   is the sum of external forces on node i and

   

3. Initial conditions: user supplies initial positions of all masses and velocities.
4. The user supplies external forces: gravity, collision forces, keyframed forces, wind, hydrodynamic resistance, etc. as a function of time.
5. Simulation.
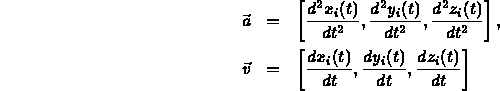
   • Factor second-order ODE into two coupled first-order ODE's:

     

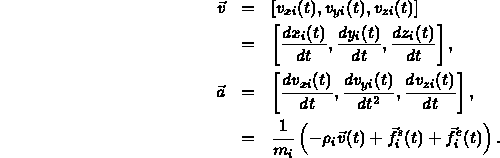
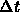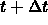   • Solve using your favourite ODE solver. The simplest technique is the Euler step: pick a . Then compute the values of all positions at from the positions at t by discretizing the differential equations: