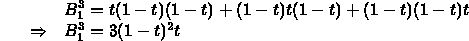- Line segment from an affine combination of points
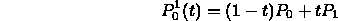
- Quadratic segment from an affine combination of line segments
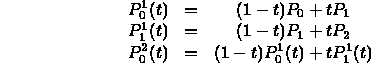
- Cubic segment from an affine combination of quadratic segments
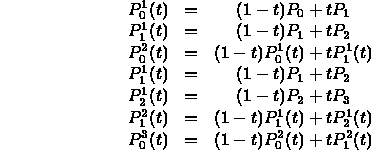
- The pattern should be evident for higher degrees.
- Join the points
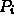 by line segments
by line segments
- Join the t : (1-t) points of those line segments by line segments
- Repeat as necessary
- The t : (1-t) point on the final line segment is a point on the curve
- The final line segment is tangent to the curve at t
- The original points appear as coefficients of Bernstein polynomials
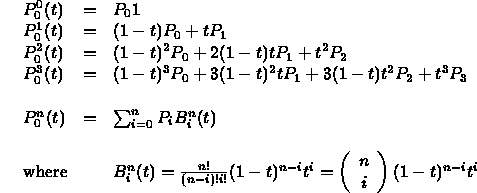
- The Bernstein polynomials of degree n form a basis for the space of all degree-n polynomials
- To obtain curve points:
- Start with given points and form succesive, pairwise, affine combinations
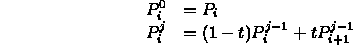
- The generated points
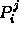 are the deCasteljau points
are the deCasteljau points
- Start with given points and form succesive, pairwise, affine combinations
- To obtain basis polynomials:
- Start with 1 and form successive, pairwise, affine combinations
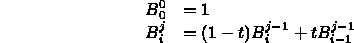
where
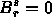 when r<0 or r>s
when r<0 or r>s
- Start with 1 and form successive, pairwise, affine combinations
- Each node gets the affine combination of the
two nodes entering from below
- Leaf nodes have the value of their respective points
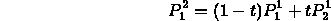
- Each node gets the sum of the path products entering
from below

- Each node gets the affine combination of the two nodes
entering from above
- Root node has value 1
- For other nodes, missing entries above count as zero
- Each node gets the sum of the path products entering from above