- Form factor specifies fraction of energy leaving one
patch that (directly) arrives at another patch.
- The differential form factor is given by
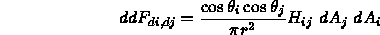
where
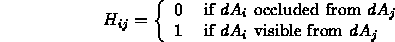
- To see how much of
 illuminates patch j, we integrate:
illuminates patch j, we integrate:
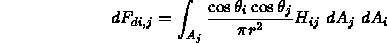
- The form factor from
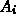 to
to 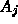 is an area average of
the integral over
is an area average of
the integral over 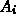 :
:
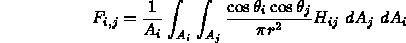
- Typically we approximate this integral:
- Hemi-sphere
- Hemi-cube
- Compute
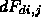
- Lots of
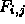 's may be zero leading to a sparse matrix
's may be zero leading to a sparse matrix
- Place a hemisphere around patch i and project patch j onto it
- Select a point on each patch and look at angles
- Project patch j onto hemisphere, and project projection
into circle:
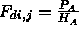 where
where 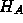 is the area of the circle.
is the area of the circle.
- In the integral for form factors
- projecting onto the hemisphere accounts
for
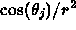
- projecting onto circle accounts for
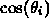
- divide by area of circle accounts for
- projecting onto the hemisphere accounts
for
- Note that any polygon with same ``cross section'' has same form factor
- Projecting onto hemisphere is still hard
- Project onto a hemi-cube
- Subdivide faces into small squares
- Now determine which squares patch j projects onto
- Each hemi-cube cell P has pre-computed delta form factor
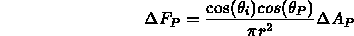
- Approximate
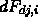 by summing delta form factors
by summing delta form factors
- If distance from i to j is large, this is good
approximation for
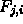 .
.
- Plus! Use z-buffer and do all patches at once to get shadows.
Have to render all patches 5 times (once for each side) using center of patch i as viewpoint.
Hack!! When scan converting a patch, use the pointer to that patch for its ``colour''
- We can compute the exact form factor for point to polygon
The differential form factor is given by
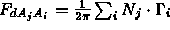 where
where
-
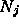 is the normal to patch j
is the normal to patch j
-
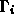 is the vector in direction
is the vector in direction 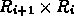 with length equal to
with length equal to 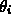 (in radians).
(in radians).
-
- Doesn't account for occlusion
- Also an exact polygon to polygon form factor but...