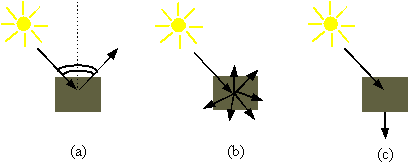
 Figura 0.1 (a)
Superfici speculari. (b) Superfici diffusive. (c) Superfici traslucide.
Figura 0.1 (a)
Superfici speculari. (b) Superfici diffusive. (c) Superfici traslucide.I modelli di illuminazione descrivono i fattori che determinano il colore di una superficie in un determinato punto, ad esempio descrivendo le interazioni tra le luci e le superfici tenendo conto delle proprietà delle superfici e della natura della radiazione luminosa incidente. Líuso di un modello di illuminazione è necessario per ottenere una rappresentazione realistica delle superfici tridimensionali. Senza un modello di illuminazione si puÚ solo assumere che ciascuna superficie sia illuminata uniformemente. Sotto questa assunzione, la proiezione ortogonale di una sfera apparir‡ come un cerchio colorato uniformemente, mentre un cubo apparir‡ come un esagono. Le immagini appaiono dunque piatte, e ciò fa perdere la natura tridimensionale degli oggetti visualizzati. Se osserviamo invece una fotografia di una sfera illuminata, quello che vediamo non è un cerchio uniformemente colorato, ma piuttosto una forma circolare con diverse gradazioni, o ombreggiature (shade), di colore. » proprio líuso sfumato del colore e dellíombreggiatura che dà alle immagini bidimensionali un aspetto tridimensionale.
A livello di modello fisico
ìesattoî, il modo in cui la radiazione luminosa
viene riflessa da una superficie dipende da:
Quando la luce colpisce la superficie, una parte
è assorbita, e una parte è riflessa.
Se la superficie è opaca, assorbimento e riflessione coinvolgono
tutta la luce che ha colpito la superficie. Se invece la superficie
è traslucida, parte della luce è trasmessa attraverso
il materiale e, una volta riemersa, andrà ad interagire
con altri oggetti. Le interazioni tra luce e materiali possono
essere classificate nei tre gruppi seguenti.
 Figura 0.1 (a)
Superfici speculari. (b) Superfici diffusive. (c) Superfici traslucide.
Figura 0.1 (a)
Superfici speculari. (b) Superfici diffusive. (c) Superfici traslucide.Oltre alla riflessione diretta della luce, si devono considerare anche le riflessioni reciproche tra gli oggetti della scena (o inter-riflessioni). Nei modelli questo effetto viene simulato sotto forma di una illuminazione uniforme della scena, chiamata illuminazione ambiente, che fa sì che nessuna superficie risulti completamente scura. Líilluminazione ambiente si assume caratterizzata da uníintensità costante in ogni punto della scena.
Il livello di realismo permesso dai diversi modelli di illuminazione varia in modo notevole, così come varia la complessità computazionale ad essi associata. Più sofisticato è il modello, maggiore è il suo costo computazionale, tanto che, in via del tutto approssimativa, si può affermare che il costo computazionale di un modello di illuminazione aumenta in modo esponenziale allíaumentare del realismo.
Nella scelta di un particolare modello di illuminazione si deve dunque valutare quale sia il più alto livello di realismo ottenibile ad un costo computazionale sostenibile dalla particolare applicazione. Le entità in gioco sono
Il modello di Phong è un semplice modello di illuminazione diventato uno standard in computer graphics per il buon compromesso tra livello di approssimazione matematica dellíinterazione fisica luce-superfici e il costo computazionale. Il modello di Phong è al tempo stesso efficiente e aderente alla realtà fisica, e consente di ottenere un buon rendering delle immagini, sotto uníampia varietà di condizioni di illuminazione e proprietà dei materiali.
Nel modello di Phong, la radiazione luminosa si considera
emessa da sorgenti puntiformi posizionate a distanza infinita
dalla scena (si parla, a questo proposito, di radiazione direzionale).
Il colore di un punto arbitrario p su una superficie viene
calcolato utilizzando quattro vettori di modulo unitario:
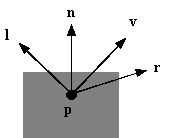 Figura 0.2 Vettori
utilizzati nel modello di Phong.
Figura 0.2 Vettori
utilizzati nel modello di Phong.Si osservi che, se la superficie è curva, questi quattro vettori possono cambiare muovendosi da un punto allíaltro.
Nel modello di Phong, la riflessione della radiazione luminosa viene modellata in termini di tre componenti additive, diffusa, speculare e ambiente, ciascuna modellata separatamente. La componente diffusa è direzionale, si riflette proporzionalmente allíangolo di incidenza con la superficie riflettente in tutte le direzioni e quindi Ë identica per tutti gli osservatori. La componente speculare è direzionale e si riflette lungo una direzione privilegiata (funzione della direzione di incidenza e della normale alla superficie). La componente ambiente si riflette in tutte le direzioni con uguale intensità ed è usata per schiarire le zone díombra. Si suppone inoltre che, ciascuna sorgente puntiforme abbia componenti separate per la luce diffusa, speculare e ambiente relative ai tre colori primari rosso, verde e blu. In corrispondenza di ciascun punto p sulla superficie, possiamo quindi calcolare una matrice di illuminazione 3 3, relativa alla i-esima sorgente luminosa:
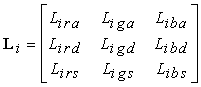
La prima riga contiene le intensità della luce ambiente, relative alle componenti red, green e blue; la seconda riga contiene le tre componenti della luce diffusa; e la terza contiene le componenti della luce speculare. Assumiamo che non siano ancora stati applicati i termini per líattenuazione dovuta alla distanza.
Per costruire il modello si suppone che sia possibile calcolare líammontare della luce incidente che viene riflessa nel punto di interesse. Ad esempio, per il termine relativo alla componente di colore rosso della luce diffusa, Lird, possiamo calcolare un termine di riflessione, Rird, il cui contributo allíintensità della luce nel punto p è Rird Lird. Il valore di Rird dipende dalle proprietà del materiale, dallíorientazione della superficie, dalla direzione della sorgente luminosa e dalla distanza tra la sorgente luminosa e líosservatore. Per ogni punto p della superficie, si calcola dunque una matrice di riflessione
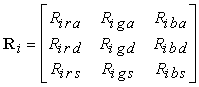
Il contributo di ciascuna sorgente luminosa si ottiene sommando le componenti ambiente, diffusa e speculare. Ad esempio, líintensità luminosa rossa che vediamo nel punto p per effetto della sorgente luminosa i è data da
Iir = RiraLira + RirdLird + RirsLirs = Iira + Iird + Iirs.
Líintensità totale si ottiene infine sommando i contributi di tutte le sorgenti, a cui si aggiunge possibilmente un termine relativo alla luce ambiente globale. Per la componente rossa risulta quindi
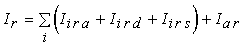
dove Iar è la componente rossa della luce ambiente globale.
Questa notazione può essere semplificata osservando che le computazioni necessarie sono identiche per ogni sorgente luminosa, e per ogni colore primario. Possiamo quindi omettere gli indici i, r, g, b, e scrivere semplicemente
I = Ia + Id + Is = RaLa + RdLd + RsLs
tenendo presente che la computazione si deve comunque fare per ogni sorgente e per ogni colore primario.
Nel modello di Phong il fenomeno della inter-riflessione diffusa tra gli oggetti della scena viene approssimato per mezzo della componente ambiente, che si assume distribuita uniformemente, con intensità La uguale in ogni punto della superficie. Parte di questa luce è assorbita, e parte è riflessa dalla superficie in base al valore del coefficiente di riflessione ambiente Ra = ka. Poiché solo una frazione positiva della luce è riflessa, abbiamo
0 ka 1
e quindi
Ia = kaLa.
Ogni superficie ha tre coefficienti ambientali ñ kar, kag e kab ñ relativi ai tre colori primari, e questi coefficienti possono anche differire tra loro.
Si osservi infine che líassunzione di distribuzione uniforme della componente ambiente costituisce una approssimazione notevole poiché non tiene conto dellíeffettiva interazione tra gli oggetti della scena.
La riflessione diffusa è la componente della radiazione luminosa riflessa da una superficie perfettamente diffusiva ugualmente verso qualsiasi direzione.
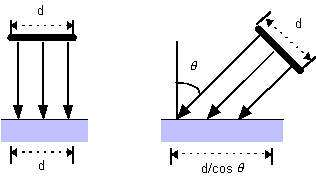
Líintensità della luce riflessa dipende dallíampiezza dellíangolo q tra la direzione di incidenza della sorgente di luce l, e la normale n alla superficie. Infatti, in accordo alla legge di Lambert, noi vediamo solo la componente verticale della luce incidente. Per comprendere almeno intuitivamente questa legge, consideriamo líesempio mostrato in Figura 0.3. Quando la sorgente luminosa si abbassa, lo stesso ammontare di luce si distribuisce su uníarea più vasta, e la superficie appare meno luminosa.
 Figura
0.3 Legge di Lambert.
Figura
0.3 Legge di Lambert.La riflessione diffusa si può dunque caratterizzare matematicamente, in accordo alla legge di Lambert, nel seguente modo
Rd = kd cos q,
dove cos q = l ï n, e kd è il coefficiente di riflessione che approssima il grado di diffusività della superficie, ossia la frazione di luce incidente che viene riflessa.
Complessivamente, il termine relativo alla riflessione diffusa risulta uguale a
Id = RdLd = kd cos q Ld = kd(l ï n) Ld
Per tenere conto dellíattenuazione della luce che viaggia dalla sorgente luminosa alla superficie, si può inoltre introdurre un termine quadratico:
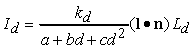
dove d è la distanza tra la sorgente e la superficie e a, b e c sono costanti. Questa attenuazione della luminosità con la distanza consente di aumentare líeffetto di profondità.
Quasi tutti i materiali possiedono un grado più o meno alto di riflessione speculare. In particolare, più la superficie di un oggetto è liscia, più il suo comportamento è simile a quello di uno specchio. Modellare una superficie speculare in modo realistico è un compito piuttosto complesso, poiché il pattern in base a cui la luce viene diffusa non è simmetrico, dipende dalla lunghezza díonda della luce incidente e cambia con líangolo di riflessione.
La riflessione speculare è modellata da Phong assumendo che, solo in prossimità della direzione r di riflessione speculare, la radiazione luminosa venga riflessa su tutto lo spettro, a prescindere dalle caratteristiche di assorbimento proprie del materiale. Líammontare di luce vista dallíosservatore dipende quindi dallíangolo f tra r e v, dove v è il vettore diretto verso líosservatore.
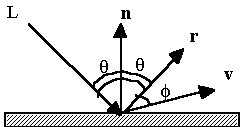 Figura 0.4 Riflessione
speculare
Figura 0.4 Riflessione
speculareNel modello di Phong si introduce un termine additivo che tiene conto della riflessione speculare, e che è dato dallíequazione
Is = ksLs cosaf.
Il coefficiente ks (0 ka 1) rappresenta la frazione di luce speculare riflessa. Líesponente a è chiamato coefficiente di brillantezza. Allíaumentare di a la luce riflessa si concentra in una regione sempre più stretta centrata sullíangolo di riflessione. Al limite, quando a tende allíinfinito, il comportamento simulato è esattamente quello di uno specchio. I valori di a compresi nellíintervallo [100, 500] corrispondono approssimativamente alle superfici metalliche, mentre i valori inferiori a 100 corrispondono ai materiali che mostrano uníampia zona di massima lucentezza.
Se i due vettori r e n sono normalizzati, possiamo utilizzare il loro prodotto scalare per definire il coseno dellíangolo f, e il termine speculare diventa
Is = ksLs (r ï v) a.
Si osservi che, anche in questo caso, il modello
è locale: si considera solo la riflessione della radiazione
luminosa proveniente dalla sorgente, e non quella potenzialmente
riflessa da altri oggetti nella scena.
Complessivamente, líequazione di illuminazione del modello di Phong risulta uguale a
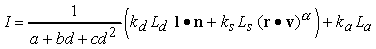
dove si è aggiunto il termine di attenuazione della luminosità allíaumentare della distanza tra la sorgente e líosservatore. Questa formula deve essere calcolata per tutte le sorgenti e per ciascun colore primario.
Riassumendo, le caratteristiche principali del modello
di illuminazione di Phong sono
Nel modello di Phong, la maggior parte del lavoro computazionale riguarda il calcolo dei quattro vettori e dei loro prodotti scalari.
Sulle superfici lisce, il vettore normale esiste in ogni punto e fornisce líorientazione locale della superficie. Il calcolo di questo vettore dipende da come la superficie è rappresentata matematicamente. Consideriamo due casi semplici: il piano e la sfera.
Un piano può essere descritto sia dallíequazione
ax + by + cz + d = 0,
che in termini della normale n e di un punto p0 appartenente al piano:
n ï (p ñ p0) = 0,
dove p è un punto qualsiasi del piano, di coordinate (x, y, z). Confrontando le due espressioni, si trova che il vettore n è dato da
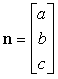
Se invece dellíequazione del piano, ci vengono dati tre punti, p0, p1 e p2, non allineati, appartenenti al piano, possiamo determinare il vettore normale calcolando il seguente prodotto vettoriale
n = (p2 ñ p0) (p1 ñ p0)
Vediamo ora come calcolare la normale alla superficie di una sfera di raggio unitario, centrata nellíorigine. Líequazione implicita di questa sfera è
f(x, y, z) = x2 + y2 + z2 ñ 1 = 0,
che, in forma vettoriale, diventa
f(p) = p ï p ñ 1 = 0.
La normale è data dal vettore gradiente
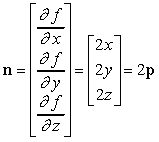
La sfera può essere rappresentata anche in forma parametrica. Le coordinate di un punto sulla sfera sono rappresentate indipendentemente in termini di due parametri u e v:
x = x(u, v)
y = y(u, v)
z = z(u, v)
Per ogni superficie ci possono essere diverse rappresentazioni parametriche. Una possibile rappresentazione parametrica per la sfera è data da
x = x(u, v) = cos u sin v
y = y(u, v) = cos u cos v
z = z(u, v) = sin u
I punti sulla sfera si ottengono al variare di u
nellíintervallo ñp/2 < u < p/2
e di v nellíintervallo ñp < v < p.
Quando si lavora utilizzando la rappresentazione
parametrica, la normale alla superficie della sfera si ottiene
considerando il piano tangente
nel punto 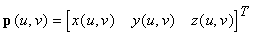
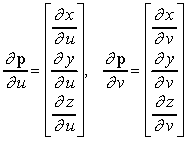
giacciono sul piano tangente. Quindi, possiamo calcolarne il prodotto vettoriale per determinare il vettore normale
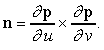
Per la sfera unitaria risulta
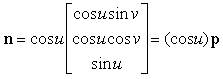
Dato che siamo interessati unicamente alla direzione, possiamo dividere per il coseno di u per ottenere il vettore normale di modulo unitario; risulta allora n = p.
Una volta determinato il vettore normale in un punto, possiamo utilizzare questo vettore, insieme alla direzione l della sorgente luminosa, per calcolare la direzione r di riflessione speculare perfetta. Come è noto, gli specchi sono caratterizzati dalla proprietà: líangolo di incidenza è uguale allíangolo di riflessione. Líangolo di incidenza qi è líangolo tra la normale e la sorgente luminosa, e líangolo di riflessione qr è líangolo tra la normale e la direzione in cui la luce è riflessa. In due dimensioni, questa condizione è sufficiente, poiché esiste un solo angolo che soddisfa la proprietà citata. Questo non è più vero in tre dimensioni, e in questo caso si aggiunge la proprietà: dato punto p sulla superficie, la luce incidente, la luce riflessa e la normale alla superficie in quel punto devono giacere nello stesso piano. Assumendo che l e n siano di modulo unitario, dalla condizione qi = qr segue
cos qi = cos qr,
e utilizzando i prodotti scalari si ottiene
cos qi = l ï n = cos qr = n ï r.
La proprietà di coplanarità implica infine che possiamo scrivere r come una combinazione lineare di l e di n:
r = a l + b n.
Calcolando il prodotto scalare col vettore n, troviamo
n ï r = a l ï n + b n ï n = a l ï n + b = l ï n
La seconda condizione si ottiene richiedendo che r sia di modulo unitario
1 = r ï r = a2 + 2 ab l ï n + b2.
Infine, risolvendo le due equazioni si ottiene
r = 2 (l ï n) n ñ l.
Le tecniche di shading sono tecniche tramite cui, dato un modello di illuminazione ed una superficie, si individua il colore di ogni singolo punto sulla superficie. Dato un insieme di sorgenti puntiformi ed un osservatore, assumendo di saper calcolare il vettore normale in ogni punto, possiamo applicare il modello di illuminazione di Phong, per determinare il colore. Tuttavia, il costo computazionale può essere molto pesante.
Per ridurre il carico di lavoro richiesto dalle tecniche di shading, la maggior parte dei sistemi grafici, compreso OpenGL, utilizza mesh di poligoni piatti per approssimare le superfici. In un mesh di poligoni piatti, infatti, ogni singolo poligono è caratterizzato da un unico vettore normale, costante in tutti i suoi punti. Analizzeremo tre diverse tecniche di shading: il flat shading, il Gouraud shading ed il Phong shading.
I tre vettori ñ l, n e v ñ possono variare muovendosi da un punto allíaltro sulle superfici. Nel caso di un poligono piatto, il vettore normale n si mantiene invece costante in tutti i punti. Anche l e v possono essere considerati costanti, se si fa líipotesi che la sorgente luminosa e líosservatore siano a distanza infinita dalla superficie.
Il flat shading è basato proprio sullíipotesi che i tre vettori siano costanti per ogni poligono. Se i tre vettori sono costanti, il colore viene calcolato una volta sola per ciascun poligono: ogni poligono è sottoposto alla scan conversion, ed ad ogni suo pixel è associato il valore calcolato sulla base dei tre vettori costanti. Ad ogni punto di un poligono è dunque assegnata la stessa gradazione di colore.
Nella libreria OpenGL, il flat shading è specificato
dalla funzione
glShadeModel(GL_FLAT);
OpenGL utilizza la normale associata al primo vertice di un singolo poligono. Per le primitive quali triangle_strip, OpenGL utilizza la normale del terzo vertice per il primo triangolo, la normale del quarto vertice per il secondo triangolo, e così via. Regole simili si applicano per le altre primitive.
La tecnica di flat shading è estremamente efficiente, poiché líequazione di illuminazione va calcolata una sola volta per ogni poligono. Tuttavia, il risultato visivo non è del tutto soddisfacente, in quanto lascia visibile la suddivisione in poligoni, senza rendere nellíimmagine líandamento della superficie approssimata geometricamente dal mesh di poligoni.
Inoltre, poichË líocchio umano ha una particolare sensibilit‡ alle piccole differenze di intensit‡, si verifica il fenomeno delle bande di Mach, per cui strisce dello stesso colore affiancate con strisce di diversa intensit‡ anzichÈ apparire uniformi sembrano variare di luminosit‡ ai confini tra le strisce.
Il Gouraud shading è basato sul modello di illuminazione di Phong. Líidea di questa tecnica è quella di definire il vettore normale nei vertici di ciascun poligono come la media pesata dei vettori normali dei poligoni del mesh che condividono quel vertice. In questo modo, la normale nel vertice approssima líandamento della superficie rappresentata in tale punto. Nellíesempio nella Figura 0.5, il vettore normale è dato da
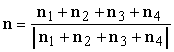
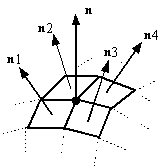 Figura
0.5 Calcolo del vettore normale nel vertice.
Figura
0.5 Calcolo del vettore normale nel vertice.Per ogni vertice si applica líequazione di illuminazione di Phong e si calcola il valore dellíintensità luminosa raggiunta da quel vertice. Ogni poligono è quindi sottoposto a scan conversion e, durante tale processo, i valori di intensità nei vertici sono interpolati bilinearmente per calcolare il valore associato ad ogni pixel.
Nella libreria OpenGL, il Gouraud shading Ë
il default ma si puÚ specificare con líinvocazione
di:
glShadeModel(GL_SMOOTH);
Dal punto di vista delle implementazioni, il Gouraud shading è mediamente efficiente, poiché líequazione di illuminazione va calcolata una sola volta per ogni vertice. Per poter individuare i vettori normali necessari per calcolare la normale nei vertici, occorre tuttavia una struttura dati che rappresenti il mesh di poligoni. Da una semplice lista di vertici, infatti, non è possibile risalire a quali poligoni condividono il vertice in esame. La struttura dati deve contenere poligoni, vertici, normali e informazioni sulle proprietà dei materiali.
Il risultato visivo prodotto dal Gouraud shading è ritenuto valido: non è visibile la suddivisione in mesh dei poligoni, e si ottiene così una rappresentazione liscia e senza discontinuità della superficie approssimata. Uno svantaggio di questa tecnica è rappresentato dal fatto che essa non permette la visualizzazione corretta della componente speculare della riflessione. Per questo motivo, il Gouraud shading è in genere usato solo ove sia sufficiente tenere conto della sola componente diffusa.
Un ulteriore problema si può verificare se la superficie non è rappresentata da un numero sufficientemente alto di facce poligonali. In questo caso, infatti, il calcolo delle normali nei vertici può far perdere i dettagli sullíeffettiva curvatura della superficie.
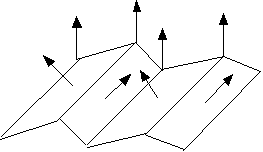 Figura 0.6 Un possibile
problema nel Gouraud shading.
Figura 0.6 Un possibile
problema nel Gouraud shading.Nella tecnica del Phong shading, invece di interpolare le intensità di colore dei vertici, come nel Gouraud shading, si interpolano le normali sui vertici di ciascun poligono per determinare la normale associata a ciascun pixel.
Per prima cosa si determinano le normali nei vertici, calcolando la media delle normali ai poligoni incidenti (la normale nel vertice approssima líandamento della superficie rappresentata in quel punto). Quindi si effettua una interpolazione bilineare sulle normali: ogni poligono è sottoposto a scan conversion; durante tale processo, le normali sui vertici sono interpolate per calcolare la normale associata ad ogni pixel. Per ogni pixel, si applica infine líequazione di illuminazione, usando la normale nel punto del poligono corrispondente al pixel, e si calcola il valore dellíintensità luminosa.
Consideriamo líesempio nella Figura 0.7. Possiamo usare le normali interpolate nei vertici A e B per interpolare le normali lungo i lati:
n(a) = (1 ñ a)nA + anB.
Lo stesso procedimento si ripete per ogni lato. Le normali nei punti interni si ottengono infine interpolando le normali dei punti sui lati, nel modo seguente:
n(a, b) = (1 ñ b)nC + bnD.
Líinterpolazione è eseguita nel corso della scan conversione del poligono, in modo che la linea tra i vertici C e D sia proiettata su una linea di scansione nel frame buffer.
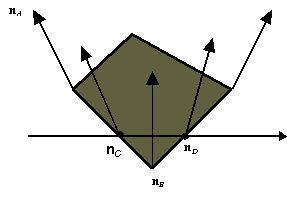 Figura
0.7 Interpolazione delle normali nel
Phong Shading.
Figura
0.7 Interpolazione delle normali nel
Phong Shading.Il Phong shading risulta più costoso in termini computazionali rispetto al Gouraud shading: si interpolano vettori e non valori interi, e líequazione di illuminazione è calcolata per ogni pixel. Mentre esistono implementazioni in hardware del Gouraud shading che consentono il suo uso in tempo reale, ciÚ non Ë vero per il Phong shading che viene normalmente svolto off-line. Il risultato visivo del Phong shading produce immagini più lisce di quelle del Gouraud shading, e permette inoltre una corretta visualizzazione della componente speculare.
La sfera non Ë un oggetto primitivo in OpenGL, ma si trova sia in GLU che in GLUT. In questa sezione svilupperemo una approssimazione poligonale alla sfera, che ci consentir‡ di illustrare líinterazione tra i parametri di ombreggiatura e líapprossimazione poligonale a superfici curve. La tecnica utilizzata Ë quella della suddivisione ricorsiva, che consente di ottenere approssimazioni di curve e superfici a qualunque livello desiderato di dettaglio.
Il punto di partenza della suddivisione sar‡
un tetraedro, ma potrebbe essere un qualunque poligono regolare.
Il tetraedro Ë formato di quattro triangoli equilateri, descritti
da quattro vertici. Utilizziamo questi valori iniziali per i vertici:
(0, 0, 1), (0, 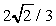
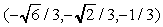
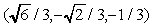
Point v[4] = {{0.0, 0.0, 1.0}, {0.0, 0.942809, -0.333333}, {-0.816497,
-0.471405, -0.333333}, {0.816497, -0.471405, -0.333333}};
Per disegnare triangoli useremo questa procedura:
void triangle(point a, point b, point c){ glBegin(GL_LINE_LOOP);
glVertex3fv(a); glVertex3fv(b); glVertex3fv(c); glEnd();}
Il tetraedro si disegna cosÏ:
void tetrahedron(void){ triangle(v[0], v[1], v[2]); triangle(v[3],
v[2], v[1]); triangle(v[0], v[3], v[1]); triangle(v[0], v[2],
v[3]);}
Líordine dei vertici segue la regola della mano destra, in modo da poter convertire con poca difficolt‡ il codice per disegnare poligoni ombreggiati.
Possiamo ottenere uníapprossimazione migliore della sfera suddividendo ciascuna faccia del tetraedro in triangoli più piccoli. La suddivisione in triangoli assicura che le nuove facce siano piane. Ci sono almeno due modi per effettuare questa suddivisione, dividendo gli angoli o dividendo i lati:
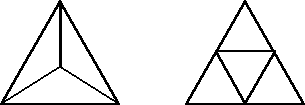 Figura 0.8 Suddivisione
di un triangolo.
Figura 0.8 Suddivisione
di un triangolo.Il primo modo perÚ non conserva i triangoli equilateri che costituivano il tetraedro regolare, perciÚ scegliamo il secondo.
Dopo aver effettuato una suddivisione di una faccia,
i quattro nuovi triangoli si trovano sullo stesso piano del triangolo
originale. Possiamo spostare i nuovi vertici sulla sfera unitaria
normalizzando ciascun vertice, mediante una semplice funzione
di normalizzazione:
void normal(point p){ double d = 0.0; int i; for (i = 0; i
< 3; i++) d += p[i]*p[i]; d = sqrt(d); if (d > 0.0) for
(i = 0; i < 2; i++) p[i] /= d;}
Adesso possiamo suddividere un triangolo, definito
dai vertici a,
b e c,
con il codice:
point v1, v2, v3;int j;for (j = 0; j < 3; j++) v1[j] = a[j]
+ b[j];normal(v1);for (j = 0; j < 3; j++) v2[j] = a[j] + c[j];normal(v2);for
(j = 0; j < 3; j++) v3[j] = c[j] + b[j];normal(v3);triangle(a,
v2, v1);triangle(c, v3, v2);triangle(b, v1, v3);triangle(v1, v2,
v3);
void tetrahedron(int n);{ divideTriangle(v[0], v[1], v[2], n);
divideTriangle(v[3], v[2], v[1], n); divideTriangle(v[0], v[3],
v[1], n); divideTriangle(v[0], v[2], v[3], n);}
divideTriangle(point a, point b, point c, int n){ if (n >
0) { point v1, v2, v3; int j; for (j = 0; j < 3;
j++) v1[j] = a[j] + b[j]; normal(v1); for (j = 0; j <
3; j++) v2[j] = a[j] + c[j]; normal(v2); for (j = 0; j <
3; j++) v3[j] = c[j] + b[j]; normal(v3); divideTriangle(a,
v2, v1, nñ1); divideTriangle(c, v3, v2, nñ1);
divideTriangle(b, v1, v3, nñ1); divideTriangle(v1,
v2, v3, nñ1); } else triangle(a, b, c);}
La libreria OpenGL consente di utilizzare quattro
tipi di sorgenti luminose:
Ciascuna sorgente deve essere definita e attivata
individualmente, e il modello di illuminazione adottato è
il modello di Phong. Le funzioni OpenGL
glLightfv(source,
parameter, pointer_to_array);glLightf(source, parameter,
value);
permettono di definire i parametri e le caratteristiche delle sorgenti. Ci sono quattro parametri vettoriali che possono essere definiti: la posizione (o direzione) della sorgente, e líammontare della luce ambiente, diffusa e speculare associata alla sorgente, distinto nelle componenti relative ai tre colori primari.
Supponiamo di voler specificare una sorgente luminosa
puntiforme, GL_LIGHT0,
disposta nel punto (1.0, 2.0, 3.0). Possiamo memorizzare
la posizione in coordinate omogenee, con il comando
Glfloat light_0_pos[ ] = (1.0,
2.0, 3.0, 1.0);
Attribuendo il valore 0 alla quarta componente, la
sorgente puntiforme diventa una sorgente distante, caratterizzata
da un vettore direzione:
Glfloat light_0_dir[ ] = (1.0,
2.0, 3.0, 0.0);
Data una sorgente, possiamo definire una componente
speculare di luce bianca, e delle componenti ambiente e diffusiva
di colore rosso utilizzando, ad esempio, il seguente codice:
Glfloat light_0_dir[ ] = (1.0,
2.0, 3.0, 0.0);Glfloat diffuse_0[ ] = (1.0,
0.0, 0.0, 1.0);Glfloat ambient_0[ ] = (1.0, 0.0, 0.0, 1.0);Glfloat
specular_0[ ] = (1.0, 1.0, 1.0, 1.0);
glEnable(GL_LIGHTING);glEnable(GL_LIGHT0);
glLightfv (GL_LIGHT0, GL_POSITION,
light_0_pos);glLightfv(GL_LIGHT0, GL_AMBIENT,
ambient_0);glLightfv(GL_LIGHT0, GL_DIFFUSE, diffuse_0);glLightfv(GL_LIGHT0,
GL_SPECULAR, specular_0);
Si osservi che è necessario attivare sia líilluminazione
che la sorgente particolare. Si può aggiungere anche un
termine globale di luce ambientale, indipendente da qualsiasi
sorgente. Se vogliamo ad esempio introdurre un lieve ammontare
di luce bianca di sfondo, possiamo utilizzare il comando
Glfloat global_ambient [ ] =
{0.1, 0.1, 0.1, 1.0};glLightModelfv(GL_LIGHT_MODEL_AMBIENT,
global_ambient);
Il fattore di attenuazione della luce dipende dalla distanza d tra la sorgente e líoggetto illuminato, ed è definito dalla funzione
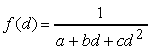
dove a è il coefficiente di attenuazione
costante, b è il coefficiente di attenuazione lineare,
e c è il coefficiente di attenuazione quadratico.
Il valore dei coefficienti è definito dai comandi
glLightf(GL_LIGHT0,
GL_CONSTANT_ATTENUATION, a);glLightf(GL_LIGHT0,
GL_LINEAR_ATTENUATION, b);glLightf(GL_LIGHT0,
GL_QUADRATIC_ATTENUATION, c);
Le sorgenti posizionali possono essere convertite in sorgenti di tipo spotlight scegliendo la direzione di spotlight (GL_SPOT_DIRECTION), líesponente e (GL_SPOT_EXPONENT), e líangolo f (GL_SPOT_CUTOFF).
Altri due parametri da ricordare sono GL_LIGHT_MODEL_LOCAL_VIEWER e GL_LIGHT_MODEL_TWO_SIDE; essi riguardano la posizione dellíosservatore (allíinterno della scena o a distanza infinita) e le caratteristiche di illuminazione differenti per le facce front e back degli oggetti, rispettivamente.
Se si suppone che líosservatore si trovi a
distanza infinita dalla scena, il calcolo dellíilluminazione
è più facile, poiché la direzione dellíosservatore
è costante in tutti i punti della scena. Per default, in
OpenGL si fa sempre questa approssimazione. Se si vuole invece
che il calcolo dellíintensità luminosa sia eseguito
utilizzando la reale posizione dellíosservatore occorre
utilizzare il comando
glLightModel(GL_LIGHT_MODEL_LOCAL_VIEWER,
GL_TRUE);
Il secondo parametro si utilizza per fare in modo
che le facce anteriore e posteriore degli oggetti siano trattate
in modo appropriato
glLightModel(GL_LIGHT_MODEL_TWO_SIDE,
GL_TRUE);
Le sorgenti luminose sono oggetti, esattamente come poligoni e punti, e quindi risultano soggette alla trasformazione OpenGL model-view. Possiamo quindi posizionare le sorgenti nella posizione desiderata, oppure in una posizione più conveniente e muoverle successivamente nella posizione desiderata attraverso una trasformazione model-view. La regola di base che governa la disposizione degli oggetti è che i vertici sono trasformati in accordo alla matrice model-view in vigore al momento della loro definizione. Con un posizionamento attento delle definizioni delle sorgenti luminose rispetto alle definizioni degli oggetti geometrici, possiamo creare sorgenti luminose che rimangono stazionarie mentre gli oggetti si muovono, sorgenti che si muovono mentre gli oggetti rimangono stazionari, e sorgenti che si muovono con gli oggetti.
Le proprietà dei materiali associati agli
oggetti della scena sono specificate attraverso le funzioni
glMaterialfv(face, type, pointer_to_array);glMaterialf(face,
value);
» possibile specificare proprietà diverse per le facce front e back di una superficie con il parametro face (GL_FRONT per la faccia anteriore, GL_BACK per la faccia posteriore, e GL_FRONT_AND_BACK se il parametro selezionato si riferisce ad entrambe le facce).
I coefficienti di riflessione ambiente, diffusa e
speculare (ka, kd e ks)
per ciascun colore primario si definiscono con tre vettori:
Glfloat ambient[ ] = {0.2, 0.2,
0.2, 1.0};Glfloat diffuse[ ] = {1.0, 0.8,
0.0, 1.0};Glfloat specular [ ] = {1.0, 1.0, 1.0, 1.0};
In questo esempio, abbiamo definito un coefficiente bianco di riflessione ambiente piuttosto basso, proprietà di diffusione gialle, e una riflessione speculare bianca.
Le proprietà dei materiali sono definite attraverso
le funzioni
glMaterialfv(GL_FRONT_AND_BACK,
GL_AMBIENT, ambient);glMaterialfv(GL_FRONT_AND_BACK,
GL_DIFFUSE, diffuse);glMaterialfv(GL_FRONT_AND_BACK, GL_SPECULAR,
specular);
Si osservi che, in questo esempio, le proprietà si riferiscono ad entrambe le facce.
La brillantezza di una superficie ñ ossia
líesponente presente nel termine relativo alla riflessione
speculare ñ è specificata dal comando
glMaterialf(GL_FRONT_AND_BACK,
GL_SHININESS, 100.0);
Le proprietà dei materiali sono modali. Il loro valore rimane quindi invariato fino a quando non viene esplicitamente modificato, e, una volta modificato, esso influenza solo le superfici definite successivamente.
Agli oggetti della scena può essere associata
una componente di luce emessa, tenendo comunque presente
che un oggetto che emette luce non è automaticamente trattato
come una sorgente luminosa. Questo termine, che non è influenzato
da nessuna delle sorgenti luminose, aggiunge una gradazione di
colore alle superfici, ed è specificato in modo simile
alle altre proprietà dei materiali. Ad esempio, per definire
un lieve ammontare di emissione luminosa blu-verde, si può
usare il codice
Glfloat emission [ ] = {0.0,
0.3, 0.3};glMaterialfv(GL_FRONT_AND_BACK,
GL_EMISSION, emission);
Per poter ombreggiare la nostra sfera con il modello
di illuminazione di OpenGL, dobbiamo assegnare le normali. Una
scelta semplice Ë di ombreggiare uniformemente ciascuna faccia,
utilizzando i suoi tre vertici per determinarne la normale e quindi
assegnare questa normale ai tre vertici. Per fare questo utilizziamo
il prodotto vettoriale e poi normalizziamo il risultato. Per il
calcolo del prodotto vettoriale usiamo la seguente procedura:
void crossProduct(point
a, point b, point c, point d){ d[0] = (b[1]
- a[1]) * (b[2] - a[2]) - (b[2] - a[2]) * (b[1] - a[1]); d[1]
= (b[2] - a[2]) * (b[0] - a[0]) - (b[0] - a[0]) * (b[2] - a[2]);
d[2] = (b[0] - a[0]) * (b[1] - a[1]) * (b[0] - a[0]); normal(d);}
Assumendo che siano state definite ed abilitate delle
sorgenti luminose, possiamo modificare la procedura triangle
per produrre sfere ombreggiate:
void triangle(point a, point b, point c){ point n; crossProduct(a,
b , c, n); glBegin(GL_POLYGON); glNormal3fv(n); glVertex3fv(a);
glVertex3fv(b); glVertex3fv(c); glEnd();}
Con questa procedura otteniamo una sfera in cui si continuano a vedere i triangoli con cui Ë approssimata.
In questo caso possiamo applicare facilmente uníombreggiatura
interpolata al modello, in quanto conosciamo la normale di ciascun
punto p sulla superficie: si tratta del vettore dallíorigine
a p. PerciÚ possiamo assegnare la vera normale a
ciascuno dei vertici e OpenGL effettuer‡ líinterpolazione
delle ombre da questi vertici attraverso líarea del rispettivo
triangolo.
void triangle(point a, point b, point c){ glBegin(GL_POLYGON);
glNormal3fv(a); glVertex3fv(a); glNormal3fv(b); glVertex3fv(b);
glNormal3fv(c); glVertex3fv(c); glEnd();}
 Figura 0.9 Ombreggiatura
con le normali esatte.
Figura 0.9 Ombreggiatura
con le normali esatte.Il risultato ottenuto usando le normali effettive Ë più realistico dellíuso dellíombreggiatura piatta, tuttavia il risultato Ë stato possibile perchÈ conoscevamo le normali in forma analitica, cosa che non Ë sempre vera in generale. Se poi volevamo creare un immagina con líombreggiatura Gouraud, avremmo dovuto sapere per ciascun vertice le normali di tutti i poligoni incidenti in quel vertice. Per fare ciÚ avremmo dovuto modificare le strutture dati del nostro programma per conservare le informazioni necessarie.
Il modello di illuminazione locale usato fin qui ha delle limitazioni. Se un oggetto blocca la luce proveniente da una sorgente, gli oggetti al di l‡ di esso restano in ombra. Se un oggetto Ë riflettente, la luce che si riflette da esso illumina altri oggetti. Un modello di illuminazione locale non puÚ produrre questi effetti nÈ produrre ombre.
Il modello di illuminazione di Phong, accoppiato alla tecnica di shading omonima, non permette la corretta rappresentazione visiva di una serie di fenomeni, quali luci o osservatore posizionati allíinterno della scena, e la valutazione delle componenti emissive e trasmissive della radiazione luminosa.
Uníulteriore limitazione del modello nasce
dal fatto che esso tiene conto solo di fenomeni locali, e quindi
non permette di modellare:
Per risolvere i problemi di
si applica il metodo Ray Tracing. Il metodo
Radiosity, invece, consente di risolvere i problemi relativi
a
Il metodo ray tracing è basato sullíosservazione che, di tutti i raggi luminosi che lasciano una sorgente, i soli che contribuiscono allíimmagine sono quelli che raggiungono líosservatore.
I raggi luminosi possono raggiungere líosservatore sia direttamente, sia per effetto delle interazioni con le altre superfici. La maggior parte dei raggi che lasciano la sorgente non raggiungerà líosservatore, e dunque non contribuirà allíimmagine. Naturalmente, non è possibile seguire la traiettoria di ciascun raggio.
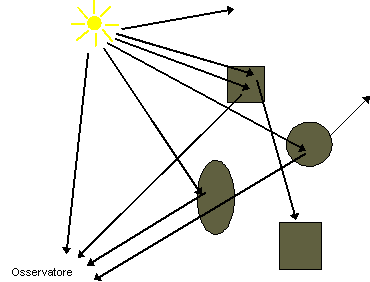 Figura 0.10 Radiazione
luminosa che lascia la sorgente.
Figura 0.10 Radiazione
luminosa che lascia la sorgente.Tuttavia, se invertiamo la traiettoria dei raggi, e consideriamo solo quelli che partono dalla posizione dellíosservatore, possiamo determinare i raggi che contribuiscono allíimmagine. Questa è esattamente líidea alla base del metodo ray tracing, che simula allíindietro il cammino compiuto dalla radiazione luminosa per giungere allíosservatore. Poiché si deve assegnare un colore a ciascun pixel, si deve considerare almeno un raggio luminoso per ogni pixel. Questo raggio è detto raggio primario.
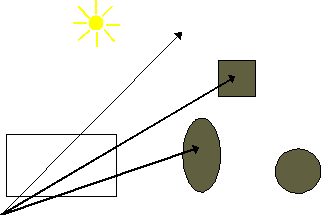 Figura 0.11 Raggi
primari associati ai pixel.
Figura 0.11 Raggi
primari associati ai pixel.Ciascun raggio primario può intersecare una superficie, o una sorgente luminosa, oppure può andare allíinfinito senza colpire nulla. Ai pixel che corrispondono allíultimo caso verrà assegnato solo un colore di sfondo. I raggi che colpiscono le superfici ñ che supponiamo opache ñ richiedono il calcolo di una gradazione di colore per il punto di intersezione.
Nel metodo ray tracing, prima di applicare il modello di riflessione, si controlla se il punto di intersezione tra il raggio primario e la superficie è illuminato. A questo scopo, si genera e si traccia un raggio ombra, diretto dal punto sulla superficie verso ogni sorgente luminosa, per calcolare se il punto di intersezione è in ombra o no rispetto alla sorgente. Se un raggio ombra interseca una superficie prima di incontrare la sorgente, la luce è bloccata e non può raggiungere il punto considerato, che rimane dunque in ombra, almeno rispetto a questa sorgente. Nessun calcolo di luminosità è necessario per le sorgenti che sono bloccate da un punto sulla superficie.
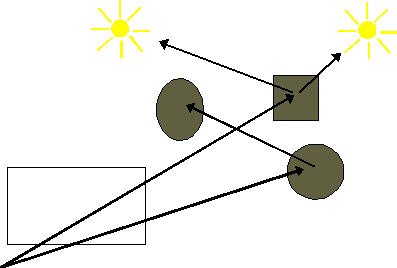 Figura 0.12 Raggi
ombra.
Figura 0.12 Raggi
ombra.Se le superfici sono tutte opache, e se non si considerano gli effetti della luce diffusa da superficie a superficie, abbiamo uníimmagine che ha, oltre allíilluminazione, anche delle ombre. Il prezzo che si deve pagare per líintroduzione delle ombre è quello di dovere effettuare un calcolo di superfici nascoste per ogni punto di intersezione tra un raggio primario e una superficie. Se alcune superfici sono invece altamente riflessive, possiamo seguire il raggio ombra, che rimbalza da una superficie allíaltra, fino a quando esso si allontana verso líinfinito, oppure interseca una sorgente.
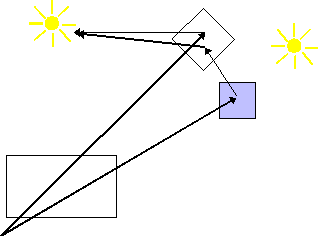 Figura 0.13 Ray
tracing con specchi.
Figura 0.13 Ray
tracing con specchi.Il metodo ray tracing consente inoltre di trattare in modo adeguato anche i casi in cui le superfici siano a trasparenza non nulla. Quando un raggio luminoso colpisce un punto di una superficie a trasparenza non nulla, la luce è parzialmente assorbita, e parte di questa luce contribuisce al termine di riflessione diffusa. Il resto della luce incidente si divide in un raggio trasmesso ed un raggio riflesso.
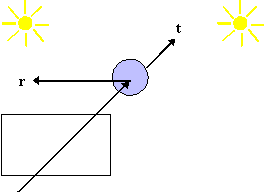 Figura 0.14 Ray
tracing con riflessione e trasmissione.
Figura 0.14 Ray
tracing con riflessione e trasmissione.
Pertanto, quando una sorgente luminosa è visibile
nel punto di intersezione tra una superficie a trasparenza non
nulla ed un raggio primario, si eseguono le operazioni seguenti:
Il raggio trasparenza e il raggio speculare sono trattati come se fossero raggi primari: sono intersecati, se possibile, con altre superfici, e terminano ad una sorgente luminosa, o allíinfinito. Ad ogni superficie intersecata, essi possono inoltre generare raggi trasparenza e speculari addizionali, e così via. Per ogni raggio primario si costruisce allora un albero di raggi, che mostra quali raggi devono essere tracciati. Líalbero è costruito dinamicamente dal processo di ray tracing.
Riassumendo, nel metodo ray tracing si eseguono le
operazioni seguenti:
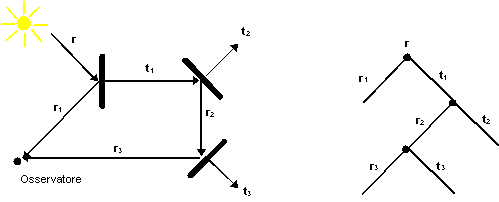 Figura 0.15 Un raggio
primario e líalbero ad esso associato.
Figura 0.15 Un raggio
primario e líalbero ad esso associato.Il metodo ray tracing può essere facilmente esteso al trattamento di primitive di output qualsiasi (ad esempio primitive solide, sfere, coni, blocchi, etc.) poiché basta dotare il metodo di un codice per il calcolo delle intersezioni tra i raggi e la nuova primitiva. Inoltre, esso gestisce correttamente la riflessione speculare tra gli oggetti poiché è basato su una modellazione globale della radiazione riflessa in modo speculare. La gestione della componente diffusa dellíilluminazione, realizzata usando un modello solo locale, non riesce invece a rappresentare i fenomeni di inter-riflessione della luce tra gli oggetti della scena.
Il metodo è tuttavia caratterizzato da un elevato costo computazionale, dovuto principalmente al calcolo delle intersezioni. Il calcolo delle intersezioni Ë problematico per molti tipi di superficie, perciÚ la maggior parte dei ray tracers trattano solo superfici piane o quadriche.
Il ray tracer usa il modello di Phong per includere un termine diffusivo al punto di intersezione tra un raggio ed una superficie. Tuttavia esso ignora la luce che viene distribuita per diffusione su quel punto, altrimenti dovrebbe considerare un tal numero di punti da diventare impossibile. PerciÚ la tecnica del ray tracing Ë più adatta per ambienti altamente riflessivi.
Il metodo radiosity è ideale per la visualizzazione delle superfici perfettamente diffusive. Senza entrare nei dettagli, vediamo solo le idee di base di questa tecnica.
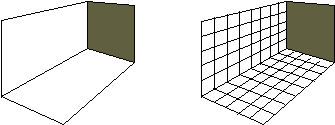 Figura 0.16 Scena
con superfici diffusive e divisione in patch.
Figura 0.16 Scena
con superfici diffusive e divisione in patch.Consideriamo una scena costituita semplicemente da due pareti perfettamente diffusive, una bianca ed una rossa. Se visualizziamo la scena supponendo di avere una sorgente luminosa distante, ogni parete assumerà un colore costante. Nella realtà, invece, la riflessione diffusa della parete rossa, colpisce la parete bianca, col risultato che della luce di colore rosso andrà ad aggiungersi alla luce bianca riflessa dalle parti di parete più vicine alla parete rossa.
Per ottenere uno shading aderente alla situazione reale in tutti i punti delle superfici, si dovrebbe risolvere uníequazione integrale molto complessa. Facendo líassunzione che le superfici siano perfettamente diffusive, si può semplificare notevolmente líequazione, ad un punto tale da poterla risolvere usando metodi numerici.
Nel metodo radiosity la scena viene suddivisa in pezze (patches), ovvero in molti poligoni piatti e di dimensioni limitate, ciascuno dei quali è considerato perfettamente diffusivo e assumerà quindi una gradazione di colore costante. Il metodo prevede due passi per determinare le gradazioni di colore da assegnare alle varie pezze. Il primo passo consiste nel determinare, per ogni coppia di pezze, i fattori di forma, che descrivono come la luce che lascia una pezza influenza líaltra. Una volta determinati i fattori di forma, líequazione integrale può essere ridotta ad un insieme di equazioni lineari per le radiosity ñ in pratica la riflessività ñ delle pezze. Dopo aver risolto queste equazioni, la scena può essere visualizzata applicando la tecnica del flat shading.
La quantit‡ di elaborazione necessaria per calcolare i fattori di forma Ë enorme ñ O(n2) con il numero n delle pezze ñ ma una volta calcolati, essi sono indipendenti dalla posizione dellíosservatore, per via dellíassunzione che tutte le superfici siano perfettamente diffusive. PerciÚ le successive operazioni di rendering di una stessa scena possono essere effettuate alla stessa velocit‡ che con líuso di un modello di illuminazione locale.