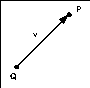
 Figura 0.1 Vettori.
Figura 0.1 Vettori.Sia nella grafica 2D che nella grafica 3D, la maggior parte degli oggetti geometrici può essere definita usando un numero limitato di entità elementari: scalari, punti e vettori.
Nonostante gli scalari non siano tipi geometrici, essi sono necessari come unità di misura. Ad esempio, la lunghezza di un segmento è uno scalare, così come il numero di gradi di cui vogliamo ruotare un oggetto.
Il punto è líoggetto geometrico fondamentale. In un sistema geometrico tridimensionale, un punto è una locazione nello spazio. Il solo attributo che un punto possiede è proprio la sua locazione, un punto matematico, infatti, non ha nemmeno una dimensione.
In fisica, il termine vettore è riferito alle quantità dotate di un modulo (o magnitudine), una direzione ed un verso. Sono vettori, ad esempio, la velocità e le forze. In computer graphics si usa disegnare i vettori come segmenti lineari orientati. I segmenti lineari soddisfano infatti la definizione di vettore: hanno una direzione, una orientazione ed un modulo (la lunghezza).
 Figura 0.1 Vettori.
Figura 0.1 Vettori.Punti e vettori esistono nello spazio indipendentemente dal sistema di coordinate di riferimento, anche se spesso risulta necessario lavorare con le loro rappresentazioni in un particolare sistema di riferimento.
Una volta definiti gli oggetti geometrici di base, è necessario definire le operazioni su questi oggetti. Le operazioni, così come gli oggetti, sono definite facendo riferimento a spazi matematici astratti. Il più importante spazio matematico è lo spazio vettoriale. Uno spazio vettoriale contiene due entità distinte: vettori e scalari. Uno spazio affine è uníestensione del concetto di spazio vettoriale che include un ulteriore tipo di oggetti: il punto. Uno spazio euclideo è uníestensione che aggiunge la nozione di distanza. In questi spazi astratti gli oggetti sono definiti indipendentemente da qualsiasi rappresentazione interna o implementazione su un particolare sistema.
Negli spazi vettoriali, i vettori possono essere rappresentati in termini di un insieme di vettori linearmente indipendenti chiamato base di vettori. Proprio questo tipo di rappresentazione costituisce il legame tra gli oggetti astratti e la loro implementazione; inoltre, la conversione tra le rappresentazioni conduce al concetto di trasformazione geometrica.
Nel seguito, utilizzeremo i numeri reali come scalari. Le operazioni fondamentali tra scalari saranno dunque le ordinarie operazioni di addizione e di moltiplicazione, con le loro operazioni inverse di sottrazione e divisione. I tipi di dati vettori e punti sono astrazioni delle entità geometriche costituite dai segmenti rettilinei orientati e dai punti nello spazio. Si utilizzerà la notazione a, b, g, Ö per gli scalari, u, v, w, Ö per i vettori, e P, Q, R, Ö per i punti.
Il modulo, o magnitudine, di un vettore v è un numero reale denotato con |v|. Si definisce vettore nullo, il vettore z tale che |z| = 0.
Líoperazione che mette in relazione scalari e vettori è la moltiplicazione, che ha la proprietà che |a| = |a| |v|, e la direzione del vettore a v è pari a quella di v, se a è positivo.
Ci sono due operazioni che mettono in relazione punti e vettori. Per prima cosa vi è la sottrazione di due punti, P e Q, operazione che definisce un vettore v:
v = P ñ Q.
Questa operazione implica che, dato un punto qualsiasi Q ed un vettore v, esiste un unico punto P che soddisfa la relazione precedente, cioè tale che
P = v + Q.
In questo modo, rimane definita una operazione di addizione tra un punto e un vettore (si veda la Figura 8.2).
 Figura
0.2 Addizione punto-vettore.
Figura
0.2 Addizione punto-vettore.Líaddizione vettore-vettore u + v si ottiene applicando la regola head-to-tail, come mostrato nella Figura 8.3: il vettore somma si disegna collegando la coda di u alla testa di v.
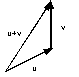 Figura
0.3 Addizione vettore-vettore.
Figura
0.3 Addizione vettore-vettore.Líaddizione di un punto e di un vettore (o la sottrazione di due punti) conduce alla nozione di linea in uno spazio affine, composta da tutti i punti della forma
P(a) = P0 + a d.
dove P0 è un punto arbitrario, d è un vettore arbitrario, e a è uno scalare. P(a) risulta dunque un punto, per ogni valore dia. Questa forma è chiamata forma parametrica della linea, poiché i punti sulla linea vengono generati variando il parametro a. Per a = 0, la linea passa per il punto P0, e al crescere di a, i punti generati giacciono nella direzione del vettore d.
Negli spazi affini non sono definite le operazioni di addizione tra due punti e di moltiplicazione di un punto per uno scalare. Esiste tuttavia uníoperazione, chiamata addizione affine, che coinvolge elementi di queste due operazioni: per ogni punto Q, per ogni vettore v e per ogni scalare positivo a,
P = Q +a v
descrive tutti i punti sulla linea che passa per Q e ha la direzione del vettore v.
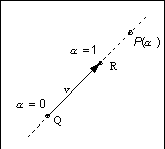 Figura 0.4 Addizione
affine.
Figura 0.4 Addizione
affine.Poiché è sempre possibile trovare un punto R tale che v = R ñ Q, avremo
P = Q + a(R ñ Q) = aR + (1 ñ a)Q.
Questa operazione, che può sembrare uníaddizione tra due punti, porta alla forma equivalente
P = a1R + a2Q
dove a1R + a2Q = 1.
Líaddizione affine permette infine di formalizzare il concetto di convessità. Un oggetto convesso è un oggetto tale che tutti i punti che giacciono sul segmento che unisce due punti al suo interno, sono a loro volta punti interni allíoggetto. Per 0 a 1, la somma affine definisce il segmento lineare che connette R e Q, e questo segmento è un oggetto convesso. Si può estendere la nozione di addizione affine per includere anche gli oggetti definiti da n punti:
P = a1P1 + a2P2 + Ö + anPn
Per induzione si può dimostrare che tale somma è definita se e solo se
a1 + a2 + Ö + an = 1.
Líinsieme di punti formato dalla somma affine
di n punti, sotto la restrizione 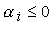
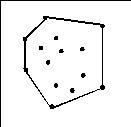 Figura 0.5 Inviluppo
convesso.
Figura 0.5 Inviluppo
convesso.Altre due operazioni fondamentali tra vettori sono il prodotto scalare e il prodotto vettoriale. Il prodotto scalare tra due vettori u e v, si denota con u ï v. Se u ï v = 0, u e v sono ortogonali. In uno spazio Euclideo, la lunghezza di in vettore Ë data da:
|u|2 = u ï u
e líangolo q tra i due vettori da:
cos q
= 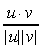
Dati tre vettori linearmente indipendenti in uno spazio tridimensionale, possiamo usare il prodotto scalare per costruire una base ortogonale di vettori. » inoltre possibile utilizzare il prodotto vettoriale tra due vettori u e v non paralleli per definirne un terzo, n, ortogonale ad entrambi:
n = u v.
La lunghezza del prodotto vettoriale d‡ il seno dellíangolo q tra u e v:
sin q
= 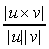
Il verso (orientazione) del vettore n si determina applicando la regola della mano destra. Nel caso tridimensionale, il prodotto vettoriale Ë dato da:
u v = 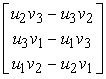
Vediamo infine la definizione di piano in uno spazio affine. » noto che tre punti, non allineati, determinano un unico piano. Supponiamo che P, Q e R, siano tre punti non allineati in uno spazio affine. Il segmento lineare che unisce P e Q è definito dallíinsieme di punti della forma
S(a) = aP + (1 ñ a)Q,
dove a è compreso tra 0 e 1. Possiamo prendere un punto arbitrario su questo segmento lineare, e definire, in modo del tutto analogo, il segmento lineare che connette tale punto con il punto R:
T(b) = bS + (1 ñ b)R,
con b compreso tra 0 e 1. Combinando le due equazioni, si ottiene líequazione del piano cui appartengono i tre punti:
T(a, b) = b[a P + (1 ñ a)Q] + (1 ñ b)R,
che può essere riarrangiata nella forma seguente:
T(a, b) = P + b(1 ñ a)(Q ñ P) + (1 ñ b)(R ñ P).
Osservando infine che Q ñ P e R ñ P sono vettori arbitrari, si dimostra che un piano può essere determinato anche da un punto P0 e da due vettori non paralleli u e v:
T(a, b) = P0 + au + bv.
Questa espressione è chiamata forma parametrica del piano, poiché fornisce il valore di un punto sul piano per ogni coppia di valori dei parametri a e b.
Se un punto P giace sul piano, allora
P ñ P0 = au + bv
quindi, usando il vettore n = u v che Ë ortogonale sia a u che a v, líequazione del piano diviene:
n ï (P ñ
P0 ) = 0.
In uno spazio vettoriale tridimensionale, è possibile rappresentare qualsiasi vettore v sulla base di tre vettori linearmente indipendenti v1, v2 e v3:
v = a1v1 + a2v2 + a3v3.
Gli scalari a1, a2 e a3 sono chiamati componenti di v rispetto alla base dei vettori v1, v2 e v3. In forma matriciale si può scrivere
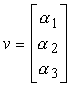
Solitamente si dice che i vettori v1, v2 e v3 definiscono un sistema di coordinate. Tuttavia, quando si devono trattare problemi che coinvolgono scalari, punti e vettori, è opportuno utilizzare un metodo più generale.
Negli spazi affini, che contengono punti, oltre a vettori e scalari, possiamo ottenere un metodo di rappresentazione più generale sostituendo un sistema di coordinate con un sistema di riferimento (frame). Un frame è definito da un insieme di vettori di base e da un punto particolare P0, líorigine. Rispetto alla nozione di spazio vettoriale, questa estensione consiste dunque nel fissare líorigine del sistema di coordinate nel punto P0. Entro un certo frame, un vettore può essere scritto in modo univoco nella forma
v = a1v1 + a2v2 + a3v3
esattamente come in uno spazio vettoriale; inoltre ogni punto può essere rappresentato univocamente come
P = P0 +b1v1 + b2v2 + b3v3.
Passando dai sistemi di coordinate ai frame, si evitano dunque le difficoltà causate dal fatto che i vettori hanno un modulo, una direzione ma non una posizione fissa. » inoltre possibile utilizzare la rappresentazione matriciale sia per i punti che per i vettori, continuando però a mantenere una distinzione tra i due oggetti geometrici.
Cambiando i vettori della base, cambia naturalmente il sistema di coordinate, e quindi la rappresentazione dei vettori. Supponiamo che {v1, v2, v3} e {u1, u2, u3} siano due basi. Ogni vettore della seconda base può essere rappresentato in termini della prima base, e vice versa. Quindi, devono esistere delle componenti scalari {aij} tali che
u1 = a11v1 + a21v2 + a31v3
u2 = a12v1 + a22v2 + a32v3
u3 = a13v1 + a23v2 + a33v3
La matrice 3 3
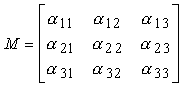
rappresenta la matrice del cambiamento di base, e la sua inversa fornisce la matrice del cambiamento dalla base {u1, u2, u3} alla base {v1, v2, v3}. Infatti se un vettore b' ha la rappresentazione [b1 b2 b3]T rispetto alla base {u1, u2, u3}, la sua rappresentazione b rispetto alla base {v1, v2, v3} soddisfa:
b = b1 u1 + b2 u2 + b3 u3 = b1(a11v1 + a21v2 + a31v3) + b2(a12v1 + a22v2 + a32v3) + b3(a13v1 + a23v2 + a33v3)
= (a11b1 + a12b 2 + a13b 3)v1 + (a21b 1 + a22b 2 + a23b 3)v2 + (a31b 1 + a32b 2 + a33b 3)v3 = M b'
e pertanto
b'
= Mñ1 b
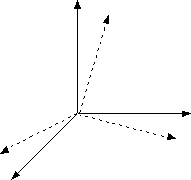 Figura 0.6 Rotazione
e scalatura di una base.
Figura 0.6 Rotazione
e scalatura di una base.
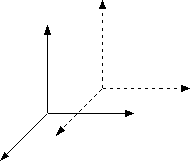 Figura
0.7 Traslazione di una base.
Figura
0.7 Traslazione di una base.Si osservi che queste variazioni della base lasciano invariata líorigine. Esse possono essere quindi utilizzate per rappresentare rotazioni e scalature di un insieme di vettori di base. Tuttavia, una semplice traslazione dellíorigine, o cambiamento di frame, non può essere rappresentata in questo modo (Figura 8.7). Per rappresentare queste operazioni è necessario introdurre le coordinate omogenee.
Supponiamo di avere un vettore b la cui rappresentazione in una base {v1, v2, v3} sia
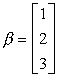
e vogliamo usare una base costituita dai tre vettori
{u1, u2, u3},
rappresentati, rispetto a {v1, v2, v3},
da:
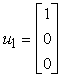
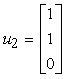
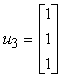
La matrice di cambiamento di coordinate Ë:
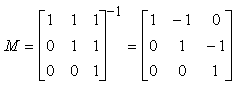
e quindi la rappresentazione di b' nel sistema {u1, u2, u3} Ë:
b = Mb
=
Se rappresentiamo un punto P di coordinate (x, y, z) con il vettore colonna
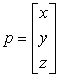
la sua rappresentazione assume la stessa forma della rappresentazione di un vettore
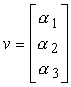
Questa situazione può generare della confusione, e rendere le implementazioni difficili. Inoltre, la moltiplicazione per una matrice in tre dimensioni non può rappresentare un cambiamento di sistema di riferimento. Con le coordinate omogenee, invece, si lavora con matrici e vettori in quattro dimensioni in modo da poter rappresentare sia punti che vettori tridimensionali. Inoltre, le operazioni tra punti e vettori possono essere eseguite usando le loro rappresentazioni in coordinate omogenee ed applicando líalgebra delle matrici
Nel frame specificato da (v1, v2, v3, P0), un punto P può essere univocamente scritto come
P = a1v1 + a2v2 + a3v3 + P0
Formalmente, questa relazione può essere rappresentata usando un prodotto tra vettori in 4 dimensioni:
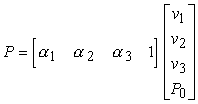
Questa espressione non rappresenta un prodotto scalare, poiché gli elementi delle matrici hanno una natura differente, tuttavia essa può essere calcolata esattamente come se fosse un prodotto scalare. Il vettore riga [a1, a2, a3 1] costituisce la rappresentazione in coordinate omogenee di un punto P. In modo equivalente, si dice che P è rappresentato dal vettore colonna
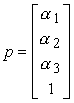
Nello stesso frame, un vettore v si può scrivere nella forma
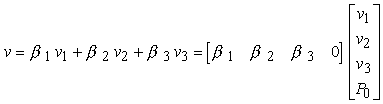
Di conseguenza v si può rappresentare col vettore colonna
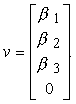
Il ricorso alle coordinate omogenee introduce altri vantaggi. Il più importante è quello che tutte le trasformazioni affini possono essere rappresentate sotto forma di moltiplicazioni di matrici in coordinate omogenee. Anche se dobbiamo lavorare in quattro dimensioni per risolvere problemi tridimensionali, usando la rappresentazione in coordinate omogenee si riduce il carico del lavoro aritmetico. La rappresentazione uniforme di tutte le trasformazioni affini rende infatti più semplice líesecuzione di trasformazioni successive. Inoltre, i sistemi hardware moderni implementano le operazioni in coordinate omogenee direttamente, utilizzando il parallelismo per velocizzare la computazione.
Una trasformazione è una funzione che mappa punti in punti o vettori in vettori. In forma funzionale si scrive
Q = T(P)
per i punti e
v = R(u)
per i vettori. Utilizzando le coordinate omogenee, si possono rappresentare sia i punti che i vettori come vettori colonna di quattro componenti ciascuno, e si può definire una trasformazione usando uníunica funzione
q = f(p)
v = f(u)
che trasforma le rappresentazioni di punti e vettori in un dato frame.
La restrizione più importante che si pone su f() è la linearità. Una funzione f() è lineare se per ogni coppia di scalari e ed ogni coppia di vertici p e q,
f(ap + bq) = af(p) + bf(q).
Le trasformazioni lineari trasformano la rappresentazione di un punto (o vettore) nella rappresentazione di un punto (o vettore), e possono essere scritte in termini delle due rappresentazioni u e v, sotto forma di una moltiplicazione di matrici:
v = M u,
dove M è una matrice quadrata. Confrontando questa espressione con quella ottenuta per le variazioni di frame, si può osservare che, se M è non singolare, ogni trasformazione lineare corrisponde ad una variazione di frame.
Quando si lavora in coordinate omogenee, M è la matrice 4 4

I 12 valori possono essere attribuiti in modo arbitrario, pertanto si dice che questa trasformazione ha 12 gradi di libertà.
Come abbiamo visto, punti e vettori hanno rappresentazioni diverse negli spazi affini. I vettori possono essere scritti nella forma
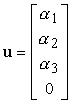
ed i punti nella forma
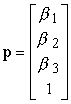
Se applichiamo una matrice arbitraria M ad un vettore, v = M u, possiamo verificare che solo 9 elementi di M influenzano u, e quindi ci sono soltanto 9 gradi di libertà nelle trasformazioni dei vettori. Le trasformazioni affini dei punti hanno invece 12 gradi di libertà.
La maggior parte delle trasformazioni che risultano necessarie in computer graphics sono affini. Esse includono rotazioni, traslazioni e scalature.
La traslazione è uníoperazione che sposta i punti di una distanza fissa, in una determinata direzione. Per specificare una traslazione, dobbiamo specificare un vettore spostamento d; i punti trasformati sono infatti dati dalla relazione
P' = P + d
per tutti i punti P dellíoggetto. Si osservi che questa definizione di traslazione non fa alcun riferimento specifico al frame o alla rappresentazione.
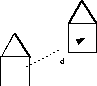 Figura 0.8 Traslazione.
Figura 0.8 Traslazione.La traslazione ha 3 gradi di libertà: possiamo infatti specificare arbitrariamente le tre componenti del vettore spostamento.
La rotazione è uníoperazione più difficile da specificare, poiché coinvolge più parametri rispetto ad una traslazione. Consideriamo prima un caso semplice: la rotazione di un angolo di un punto di coordinate (x, y) intorno allíorigine (caso bidimensionale). Indichiamo con (xí, yí) la nuova posizione del punto.
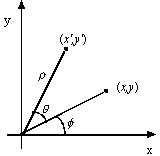 Figura 0.9 Rotazione
bidimensionale.
Figura 0.9 Rotazione
bidimensionale.Possiamo ottenere le equazioni che descrivono la rotazione rappresentando (x, y) e (x', y') in coordinate polari:
x = r cos f
y = r sin f
x' = r cos (q + f)
y' = r sin (q + f)
Applicando le identità trigonometriche relative al seno e al coseno della somma di due angoli, si ottiene
x' = r cos f cos q ñ r sin f sin q = x cos q ñ y sin q
y' = r cos f sin q + r sin f cos q = x sin q + y cos q
Queste equazioni possono essere scritte in forma matriciale nel modo seguente:
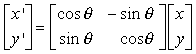
Possiamo fare subito alcune osservazioni:
Queste osservazioni possono essere utilizzate per definire in modo generale una rotazione tridimensionale indipendente dal frame. Dobbiamo specificare tre entità: il punto fisso (Pf), líangolo di rotazione (q), ed una linea o un vettore (v) attorno a cui eseguire la rotazione. Per ogni punto fisso ci sono tre gradi di libertà: i due angoli necessari per specificare líorientazione del vettore e líangolo che specifica líammontare della rotazione attorno a tale vettore.
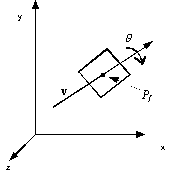 Figura 0.10 Rotazione
tridimensionale.
Figura 0.10 Rotazione
tridimensionale.Rotazioni e traslazioni sono note come trasformazioni di corpo rigido, in quanto non alterano forma e dimensioni degli oggetti, ma solo la loro posizione ed il loro orientamento.
La scalatura (o trasformazione di scala) è una trasformazione affine, non di corpo rigido. Il suo effetto è quello di modificare le dimensioni degli oggetti. La scalatura si dice uniforme se le variazioni di dimensione dellíoggetto sono uguali in tutte le direzioni.
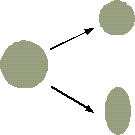 Figura 0.11 Scalatura
uniforme e non uniforme.
Figura 0.11 Scalatura
uniforme e non uniforme.Anche le trasformazioni di scala hanno un punto fisso. Quindi, per specificare una scalatura occorre specificare il punto fisso, la direzione in cui applicare la trasformazione, ed il fattore di scala (). Per a > 1, líoggetto viene ingrandito nella direzione specificata; per 0 a < 1, líoggetto diviene più piccolo nella direzione specificata. I valori negativi di definiscono le riflessioni rispetto al punto fisso e nella direzione di scalatura.
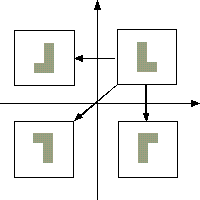 Figura 0.12 Riflessioni.
Figura 0.12 Riflessioni.Nelle applicazioni grafiche non è possibile lavorare con rappresentazioni ad alto livello, come líespressione Q = P + v. Si lavora invece facendo riferimento alla rappresentazione in coordinate omogenee, e quindi con espressioni del tipo q = p + v. Lavorando rispetto ad un frame, le trasformazioni affini risultano rappresentate da una matrice 4 4 della forma

Se muoviamo il punto p nel punto p', e se indichiamo con d il vettore spostamento, allora otteniamo la relazione
p' = p + d.
Se consideriamo le espressioni in coordinate omogenee
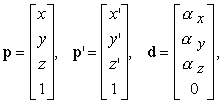
possiamo riscrivere líequazione della trasformazione componente per componente:
x' = x + ax
y' = y + ay
z' = z + az
Si può inoltre scrivere
p' = T p,
dove T è la matrice
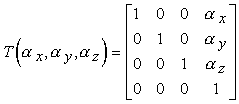
La matrice T(ax, ay, az) è chiamata matrice di traslazione, e ax, ay, az rappresentano i tre parametri indipendenti della traslazione.
La matrice inversa della matrice di traslazione si può ottenere semplicemente osservando che se applichiamo uno spostamento d ad un punto, possiamo ritornare alla posizione originaria applicando esattamente lo spostamento -d. Risulta dunque
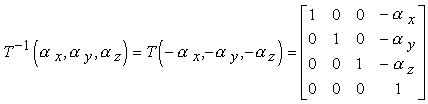
Come le rotazioni, anche le trasformazioni di scala hanno un punto fisso che rimane invariato nel corso della trasformazione. Supponiamo che il punto fisso coincida con líorigine. Le equazioni che definiscono le scalature lungo i tre assi coordinati sono
x' = bx x
y' = by y
z' = bz z
Combinando le tre equazioni, si ottiene la seguente espressione
p' = S p,
dove
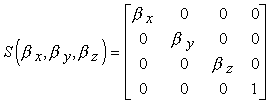
La matrice inversa della matrice di scalatura si può ottenere applicando i reciproci dei fattori di scala:
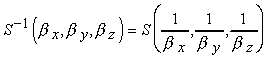
Consideriamo per prima cosa le rotazioni con punto fisso nellíorigine. Ci sono tre gradi di libertà, relativi alla possibilità di ruotare indipendentemente attorno ai tre assi coordinati. Si deve comunque prestare una certa attenzione in quanto la moltiplicazione di matrici non è uníoperazione commutativa, quindi cambiando líordine di applicazione delle tre rotazioni, può cambiare la rotazione finale risultante.
In tre dimensioni, i valori della componente z rimangono invariati per effetto di una rotazione di un angolo attorno allíasse z. La rotazione è dunque bidimensionale: i punti ruotano nei piani in cui z è costante. Si ottengono così le equazioni:
x' = x cos q ñ y sin q
y' = x sin q + y cos q
z' = z
che, in forma matriciale, diventano
p' = Rz p,
dove
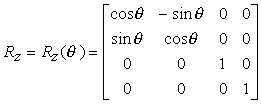
Le matrici relative alle rotazioni attorno allíasse x ed attorno allíasse y si ricavano in modo del tutto analogo:
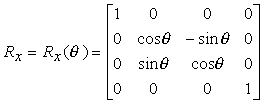
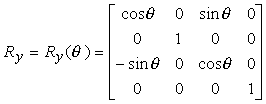
Se indichiamo con R() una qualsiasi delle tre matrici di rotazione, ed osserviamo che líeffetto di una rotazione di un angolo può essere annullato applicando la rotazione -, abbiamo che
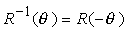
Possiamo inoltre osservare che, dato che i termini col coseno sono sempre sulla diagonale, applicando le identità trigonometriche cos (-) = cos () e sin (ñ) = ñ sin (), si ottiene
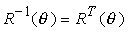
e ciò implica che le matrici di rotazione sono matrici ortogonali. Questa relazione vale anche per le rotazioni arbitrarie. Una rotazione arbitraria attorno allíorigine può essere scomposta in tre rotazioni successive attorno agli assi coordinati:
R = Rx Ry Rz
e, poiché la trasposta di un prodotto è data dal prodotto delle trasposte in ordine inverso, risulta
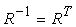
Le deformazioni sono trasformazioni indotte dai coefficienti non diagonali delle matrici di trasformazione. Come tutte le trasformazioni affini, anche le deformazioni possono essere costruite usando rotazioni, traslazioni e scalature; tuttavia data la loro importanza, le deformazioni sono spesso trattate come trasformazioni di base.
Vediamo come esempio il caso di una deformazione nella direzione dellíasse x. Questa deformazione lascia invariate le coordinate y e z dei punti dellíoggetto deformato, e viene pertanto chiamata deformazione yz. La deformazione è caratterizzata da un angolo q, e le equazioni della trasformazione sono
x' = x + y cot q
y' = y
z' = z
Queste equazioni conducono alla seguente matrice di deformazione
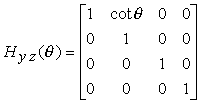
La matrice inversa si ricava dalla relazione
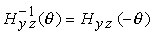
Vediamo ora come creare altre trasformazioni affini moltiplicando tra loro, o concatenando, le trasformazioni di base.
Supponiamo di eseguire tre trasformazioni successive su un punto p, creando in questo modo il punto q. Dato che il prodotto tra matrici è associativo, possiamo scrivere la sequenza come
q = C B A p
senza parentesi.
Líordine in cui vengono eseguite le trasformazioni può influenzare líefficienza della computazione. Possiamo eseguire prima la trasformazione A, quindi la trasformazione B ed infine la trasformazione C. Se dobbiamo trasformare un solo punto, questo ordine è il più efficiente, poiché ogni moltiplicazione di matrice coinvolge una moltiplicazione matrice-vettore. Un secondo approccio consiste invece nel calcolare prima la matrice M = C B A, e quindi nellíapplicare la matrice M ai punti da trasformare: q = M p. Anche se dobbiamo compiere del lavoro aggiuntivo nella fase iniziale, per il calcolo della matrice M, questo secondo approccio è preferibile al primo quando i punti da trasformare sono molti.
Come primo esempio di concatenazione di trasformazioni di base, consideriamo il caso delle rotazioni con punto fisso arbitrario.
Consideriamo un cubo di centro pf, allineato agli assi x, y, z, e supponiamo di voler effettuare una rotazione di un angolo q attorno allíasse z, con punto fisso in pf. Possiamo applicare la seguente strategia: prima trasliamo il cubo in modo da far coincidere il suo centro pf con líorigine; quindi applichiamo la matrice di rotazione Rz(q), ed infine trasliamo líoggetto ruotato, riportandone il centro nel punto pf. In termini delle trasformazioni affini di base, la prima trasformazione coinvolta è una traslazione T(ñpf), la seconda una rotazione Rz(q), e líultima una traslazione T(pf):
M = T(pf) Rz(q) T(ñpf)
Moltiplicando le tre matrici risulta infine
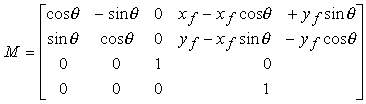
Una rotazione arbitraria intorno allíorigine si puÚ ottenere per composizione di rotazioni successive intorno ai tre assi.
R = RxRyRz
Il caso delle rotazioni attorno ad un asse arbitrario è più complesso. Ci sono tre entità da specificare: il punto fisso p0, il vettore v che dà la direzione dellíasse di rotazione, ed infine líangolo di rotazione q. Generalmente il vettore v si prende di modulo unitario:
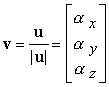
La prima trasformazione da effettuare è la traslazione del punto fisso nellíorigine T(ñp0), mentre la trasformazione finale sarà T(p0). La rotazione attorno al vettore v può essere scomposta in tre rotazioni. La strategia che si applica è la seguente: si eseguono prima due rotazioni per allineare líasse v allíasse z. Quindi si esegue una rotazione di un angolo q attorno allíasse z, ed infine si cancella líeffetto delle prime due rotazioni. La matrice complessiva di rotazione sarà dunque
R = Rx(ñqx) Ry(ñqy) Rz(ñq) Ry(qy) Rx(qx)
Per determinare i due angoli di rotazione qx e qy, osserviamo per prima cosa che
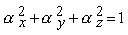
in quanto v è un vettore unitario. Se indichiamo con fx, fy e fz gli angoli tra il vettore v e i tre assi coordinati, risulta
cos = ax
cos fy = ay
cos fz = az
Dei tre angoli fx, fy e fz solo due sono indipendenti poiché
cos2 fx + cos2 fy + cos2 fz = 1.
Questi angoli possono essere utilizzati per determinare qx e qy. Si può infatti dimostrare che
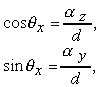
dove 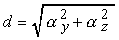
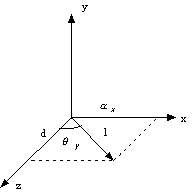
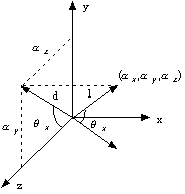 Figura
0.13 Calcolo della rotazione x.
Figura
0.13 Calcolo della rotazione x.Risulta dunque
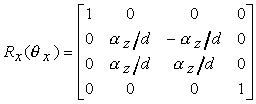
Analogamente si ricava (si veda la Figura 8.14).
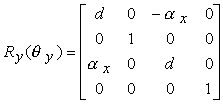
 Figura
0.14 Calcolo della rotazione y.
Figura
0.14 Calcolo della rotazione y.Infine, concatenando le varie matrici otteniamo
M = T(p0) Rx(ñqx) Ry(ñqy) Rz(q) Ry(qy) Rx(qx) T(ñp0)
Vediamo ora come implementare le trasformazioni affini usando la libreria grafica OpenGL. Useremo la matrice model-view, e la funzione glMatrixMode per selezionare la matrice a cui applicare le operazioni.
Si definisce matrice corrente di trasformazione (in breve CTM, dallíinglese current transformation matrix) la matrice che viene applicata ad ogni vertice definito successivamente nel corso dellíelaborazione. Se cambiamo la matrice CTM, cambiamo lo stato del sistema. Se p è un vertice definito dopo il setting della matrice CTM C, verrà prodotto il punto C p.
La matrice CTM è una matrice 4 4, che inizialmente coincide con la matrice identica:
C ¨ I.
Nel corso dellíelaborazione C può essere alterata da una serie di funzioni fornite dal pacchetto grafico. Le tre trasformazioni previste dalla quasi totalità dei pacchetti grafici sono traslazioni, scalature con punto fisso nellíorigine e rotazioni con punto fisso nellíorigine. Possiamo scrivere queste operazioni in forma postmoltiplicativa, ossia moltiplicando a destra:
C ¨ C T,
C ¨ C S,
C ¨ C R,
oppure nella forma
C ¨ T,
C ¨ S,
C ¨ R.
La maggior parte dei sistemi permette di caricare inizialmente la matrice CTM con una matrice arbitraria, o di postmoltiplicarla per una matrice arbitraria M:
C ¨ M,
C ¨ C M.
Nella libreria OpenGL, la matrice che viene applicata
a tutte le primitive è il prodotto della matrice model-view
(GL_MODELVIEW)
e della matrice di proiezione (GL_PROJECTION).
Dunque, la matrice CTM è data dal prodotto di queste due
matrici, e ciascuna di esse può essere manipolata individualmente
selezionando la matrice desiderata con il comando glMatrixMode.
La matrice selezionata può essere caricata con una delle
funzioni seguenti
glLoadIdentity();glLoadMatrixf(pointer_to_matrix);
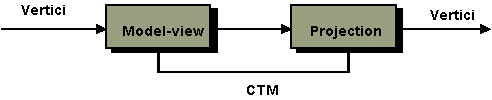 Figura 0.15 Matrici
Model-view e projection.
Figura 0.15 Matrici
Model-view e projection.
La matrice selezionata può essere alterata
attraverso il comando
glMultMatrixf(pointer_to_matrix);
Rotazioni, traslazioni e scalature sono infine implementate
dalle tre funzioni
glRotatef(angle, vx, vy, vz);glTranslatef(dx,
dy, dz);glScalef(sx, sy, sz);
Le tre funzioni modificano la matrice selezionata per postmoltiplicazione. Per le rotazioni, líangolo è specificato in gradi, e le variabili vx, vy e vz sono le componenti del vettore v che specifica la direzione dellíasse di rotazione. Nella funzione di traslazione, le variabili rappresentano le componenti del vettore di spostamento. Nelle scalature, infine, le variabili determinano i fattori di scala lungo gli assi coordinati.
Vediamo come esempio líimplementazione di
una rotazione attorno ad un punto fisso arbitrario. Supponiamo
che líangolo di rotazione sia di 45_ e che la rotazione
avvenga attorno alla linea che passa per líorigine e per
il punto (1, 2, 3), con punto fisso in (4, 5, 6):
glMatrixMode(GL_MODELVIEW)glLoadIdentity();glTranslatef(4.0,
5.0, 6.0);glRotatef(45.0, 1.0, 2.0, 3.0);glTranslatef(-4.0, -5.0,
-6.0);
Si osservi líordine: in OpenGL líultima trasformazione specificata è la prima ad essere applicata. Ciò è conseguenza del fatto che la matrice CTM viene sempre postmoltiplicata.
Infatti la sequenza di operazioni indicate Ë stata:
C ¨ I
C ¨ C T(4, 5, 6)
C ¨ C R(45, 1, 2, 3)
C ¨ C T(ñ4, ñ5, ñ6)
pertanto líeffetto complessivo Ë il seguente:
C ¨ T(4, 5, 6) R(45, 1, 2, 3) T(ñ4, ñ5, ñ6)
void
display(void){ glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glLoadIdentity(); glRotatef(theta[0], 1, 0, 0); glRotatef(theta[1],
0, 1, 0); glRotatef(theta[2], 0, 0, 1); colorcube(); glFlush();
glutSwapBuffers();}
void mouse(int btn, int state, int
x, int y){ if (btn == GLUT_LEFT_BUTTON & state
== GLUT_DOWN) axis = 0; if (btn == GLUT_MIDDLE_BUTTON
& state == GLUT_DOWN) axis = 1; if (btn == GLUT_RIGHT_BUTTON
& state == GLUT_DOWN) axis = 2;}
void spinCube(){ theta[axis] += 2; if (theta[axis]
> 360) teta[axis] -= 360; display();}