 Figura 0.1 Formazione
dellíimmagine nel modello synthetic-camera.
Figura 0.1 Formazione
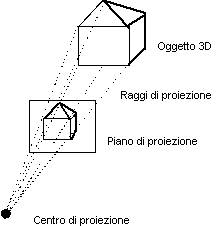
dellíimmagine nel modello synthetic-camera.I fondamenti concettuali della computer graphics tridimensionale sono basati su modelli di sistemi ottici. Il processo di formazione delle immagini generate dal computer viene assimilato al processo di formazione di uníimmagine da parte di un sistema ottico, quale ad esempio una macchina fotografica. Questo paradigma Ë chiamato Synthetic-Camera Model.
Il processo di trasformazione usato per ottenere la scena che si vuole vedere Ë analogo a prendere una foto con una macchina fotografica. I passi da svolgere sono i seguenti:
Líimmagine di un punto di un oggetto tridimensionale si trova tracciando una linea, chiamata raggio di proiezione, dal punto al centro della lente del sistema ottico, chiamato centro di proiezione. Si osservi che il centro di proiezione definisce líorigine del frame della camera. Nel nostro modello, la ëpellicola fotograficaí è idealmente ëspostataí davanti alla lente, ed è chiamata piano di proiezione. Líimmagine dellíoggetto tridimensionale risulta così definita dallíintersezione tra i raggi di proiezione, provenienti dal centro di proiezione, ed il piano di proiezione.
 Figura 0.1 Formazione
dellíimmagine nel modello synthetic-camera.
Figura 0.1 Formazione
dellíimmagine nel modello synthetic-camera.Un aspetto importante che deve essere preso in considerazione è quello che riguarda le dimensioni limitate delle immagini. Nel piano di proiezione viene posta una finestra di clipping che agisce esattamente come una finestra attraverso cui líosservatore, che si trova nel centro di proiezione, osserva il mondo. Gli oggetti che appariranno nellíimmagine sono determinati dalla locazione del centro di proiezione, dalla locazione e dallíorientazione del piano di proiezione e dalle dimensioni della finestra di clipping.
In computer graphics, così come nella grafica classica, líosservatore può trovarsi allíinfinito. Muovendo il centro di proiezione allíinfinito, la proiezione diventa parallela, e la nozione di centro di proiezione è sostituita dalla nozione di direzione di proiezione. In questo caso, la dimensione dellíimmagine rimane invariata, anche se líosservatore è a distanza infinita dallíoggetto osservato.
Le proiezioni con centro di proiezione finito sono chiamate proiezioni prospettiche, mentre quelle con centro di proiezione allíinfinito sono dette proiezioni parallele.
Complessivamente, le proiezione che abbiamo definito sono dette proiezioni planari in quanto la superficie di proiezione è un piano e i raggi di proiezione sono rettilinei.
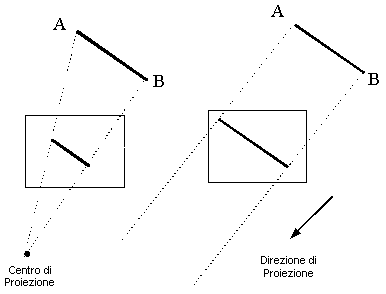 Figura 0.2 Proiezioni
prospettiche e parallele.
Figura 0.2 Proiezioni
prospettiche e parallele.In OpenGL le trasformazioni viewing e modeling sono inestricabilmente correlate ed infatti sono combinate in uníunica matrice modelview. Comprendere gli effetti combinati di queste trasformazioni tridimensionali costituisce una dei principali difficolt‡ per chi si avvicina alla computer graphics. Infatti ci sono diversi modi di pensare a queste trasformazioni: si vuole muovere la macchina in una certa direzione o muovere gli oggetti nella direzione opposta? Ciascuno modo di vedere le cose ha i suoi vantaggi e certe volte una scelta puÚ risultare più naturale per descrivere líeffetto desiderato.
Nella maggior parte dei casi, si pensa prima a come costituire la scena e poi al punto di ripresa. Ma poichÈ in OpenGL le trasformazioni vengono applicate nellíordine opposto in cui appaiono nel codice, normalmente le trasformazioni di viewing appaiono prima di quelle di modeling.
In OpenGL, per default gli oggetti e la macchina fotografica sono piazzati nellíorigine con la macchina rivolta nella direzione delle coordinate z negative. Abbiamo visto nel capitolo precedente quali trasformazioni abbiamo a disposizione per creare la scena. Vediamo adesso come effettuarne la ripresa.
Consideriamo il seguente esempio. Vogliamo visualizzare un parallelopipedo ottenuto allungando un cubo nella direzione y.
 Figura 0.3
Figura 0.3
La trasformazione di modeling che applichiamo Ë
la seguente:
glScalef(1, 2, 1);
Per poter vedere il parallelopipedo da un certa distanza,
dobbiamo spostare indietro la macchina di 5 unit‡ nella direzione
z, mediante una glTranslatef().
Quindi per visualizzare líoggetto in prospettiva, utilizziamo
una trasformazione proiettiva con glFrustum().
void display (void){
Ö glLoadIdentity(); glTanslatef(0, 0, -5); glScalef(1,
2, 1); auxWireCube(1); glMatrixMode(GL_PROJECTION); glFrustum(-1,
1, -1, 1, 1.5, 20); glMatricMode(GL_MODELVIEW); glFlush();}
Una trasformazione di viewing cambia la posizione e líorientazione del punto di vista. Un primo modo per effettuarla Ë usando una o più comandi di modeling. Gli effetti di queste trasformazioni si possono considerare sia come spostamenti della macchina o spostamenti degli oggetti nella scena rispetto ad una macchina fissa.
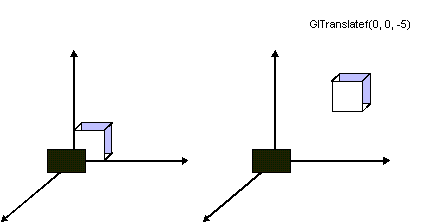 Figura 0.4 Disposizione
della macchina
Figura 0.4 Disposizione
della macchina
Un altro modo per definire la posizione della macchina
Ë tramite la primitiva gluLookAt().
Ad essa vanno forniti tre gruppi di argomenti che specificano
la posizione della macchina, un punto verso il quale la macchina
Ë puntata e un punto che indica la direzione verso líalto:
gluLookAt(Gldouble eyex, Gldouble
eyey, Gldouble eyez,Gldouble centrex, Gldouble
centrey, Gldouble centrez,Gldouble upx, Gldouble upy, Gldouble
upz)
Una soluzione alternativa è quella di descrivere
posizione ed orientamento della camera rispetto al frame esterno.
Il tipo di immagine che si vuole ottenere ñ prospettiva
o parallela ñ è determinato separatamente tramite
la matrice projection. Questa parte del processo di viewing è
spesso chiamata trasformazione di normalizzazione. Anche
in questo caso, la camera si immagina inizialmente posizionata
nellíorigine, diretta verso le z negative. La posizione
desiderata è centrata nel punto chiamato punto di riferimento
per la vista (in breve VRP dallíinglese view
reference point), la cui posizione è data rispetto
al frame esterno. Líutente esegue dunque la funzione
set_view_reference_point(x, y,
z);
per specificare la posizione del VRP. Per definire
líorientazione della camera si specificano la normale
al piano di vista (in breve VPN dallíinglese
view-plane normal) ed il vettore view-up (in breve
VUP). Il VPN definisce líorientazione del piano
di proiezione:
set_view_plane_normal(nx, ny,
nz);
Per fissare la direzione della camera si esegue la
funzione
set_view_up(ux, uy, uz);
Proiettando il vettore VUP sul piano di vista si ottiene il vettore v, detto vettore di up-direction. Il vettore v è ortogonale al vettore VUN n. Calcolando il prodotto vettoriale tra v e n possiamo definire una terza direzione, ortogonale alle prime due, u. Le tre direzioni ortogonali v, n, e u definiscono il sistema di coordinate di viewing. Aggiungendo il VPR rimane dunque definito il frame della camera.
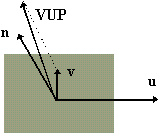 Figura 0.5 Frame
della camera.
Figura 0.5 Frame
della camera.Supponiamo di essere nel frame della camera, con la camera nellíorigine, diretta verso le coordinate z negative. Consideriamo i casi più semplici di proiezioni prospettiche e parallele: le proiezioni prospettiche con piano di proiezione perpendicolare allíasse z, e le proiezioni parallele ortogonali.
Nel primo caso, líeffetto della proiezione è quello di spostare il punto in posizione (x, y, z) lungo il raggio di proiezione e di portarlo nella nuova posizione (xp, yp, zp).
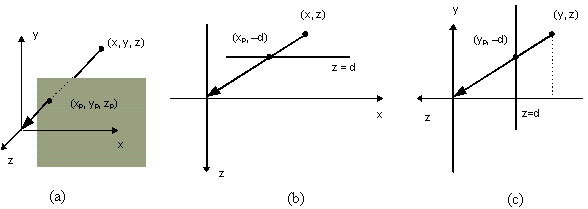 Figura 0.6 Tre visioni
delle proiezioni prospettiche: (a) tridimensionale; (b) superiore;
(c) laterale.
Figura 0.6 Tre visioni
delle proiezioni prospettiche: (a) tridimensionale; (b) superiore;
(c) laterale.Tutti i raggi di proiezione passano dallíorigine, e dato che la camera punta verso le coordinate z negative, il piano di proiezione ñ perpendicolare allíasse z ñ si trova nel semispazio negativo z < 0. Risulta dunque
zp = ñd
Per la vista superiore, risulta
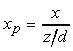
e per la vista laterale
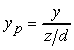
Si osservi che le equazioni sono non lineari. La divisione per z produce líeffetto prospettico per cui le immagini di oggetti più lontani dal centro di proiezione sono ridotte di dimensione rispetto alle immagini degli oggetti più vicini.
La proiezione Ë una trasformazione che preserva le linee ma non Ë affine nÈ reversibile: poichÈ tutti i punti su una linee finiscono nello stesso punto, non si puÚ ricostruire un punto dalla sua proiezione. Per rappresentare le proiezioni come matrici, occorre modificare leggermente líuso delle coordinate omogenee. Finora rappresentavamo un punto in tre dimensioni (x, y, z) con il punto in coordinate omogenee (x, y, z, 1). Se invece rappresentiamo (x, y, z) con (wx, wy, wz, w), con w 0, facciamo corrispondere ad un punto in 3 dimensioni una linea in quattro dimensioni. Il punto in tre dimensioni si puÚ ricavare dividendo le prime tre componenti per w.
Con questa estensione, si riesce a rappresentare anche le proiezioni con matrici 4 4. La matrice
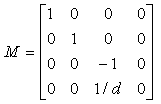
trasforma il punto p = (x, y, z, 1) nel punto q = (x, y, ñz, z/d). Se normalizziamo questo punto dividendo per la sua quarta componente (z/d), otteniamo
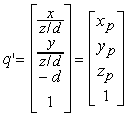
Possiamo quindi usare la matrice M per rappresentare la proiezione, a patto che alla fine effettuiamo una divisione prospettica, inserendola ad esempio come ulteriore passo nella pipeline grafica:
 Figura 0.7 Pipeline
di proiezione.
Figura 0.7 Pipeline
di proiezione.Le proiezioni ortogonali sono un caso speciale di proiezioni parallele che si verifica quando il piano di proiezione è perpendicolare alla direzione di proiezione.
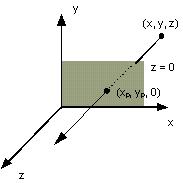 Figura
0.8 Proiezione ortogonale.
Figura
0.8 Proiezione ortogonale.Supponiamo che il piano di proiezione sia il piano z = 0 (come nellíesempio nella Figura 0.6). I punti proiettati mantengono in questo caso le proprie coordinate x e y, e le equazioni della proiezione risultano
xp = x
yp = y
zp = 0
Utilizzando le coordinate omogenee si ottiene
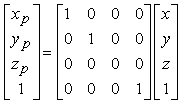
Queste semplici proiezioni possono essere utilizzate per generare proiezioni più generali secondo la seguente strategia: si applica una sequenza di trasformazioni per convertire il caso generale in uno dei due casi esaminati, e quindi si eseguono le proiezioni semplici. Prima di occuparci di questo aspetto, è opportuno esaminare come specificare le proiezioni usando la libreria OpenGL.
Le proiezioni che abbiamo appena esaminato non tengono conto delle dimensioni limitate della camera (la lunghezza focale della lente o la dimensione della pellicola): solo gli oggetti che si trovano allíinterno dellíangolo di visualizzazione della camera appariranno nellíimmagine. Più precisamente, si può definire un volume di visualizzazione che contiene gli oggetti che saranno visualizzati. Si tratta di una piramide semi-infinita, con apice nel centro di proiezione. Questo volume consente dunque di definire gli effetti del clipping delle immagini.
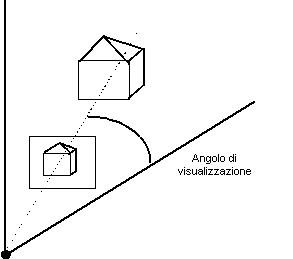 Figura 0.9 Definizione
del volume di visualizzazione.
Figura 0.9 Definizione
del volume di visualizzazione.In molte interfacce grafiche i parametri di clipping vengono definiti tramite la specificazione di una proiezione. Per definire un volume di clipping finito, si specificano, oltre allíangolo di visualizzazione, anche due piani di clipping: uno anteriore ed uno posteriore. Il volume di clipping che ne risulta è una piramide troncata, che viene detta frustum.
La libreria OpenGL mette a disposizione due funzioni per specificare le proiezioni prospettiche, ed una per specificare le proiezioni parallele. E' inoltre possibile definire la matrice di proiezione sia in modo diretto, cioè caricandola, che in modo indiretto, applicando una sequenza di trasformazioni affini alla matrice identità.
La funzione che consente di fissare il volume di
visualizzazione è la funzione
glFrustum(xmin, xmax, ymin, ymax,
zmin, zmax);
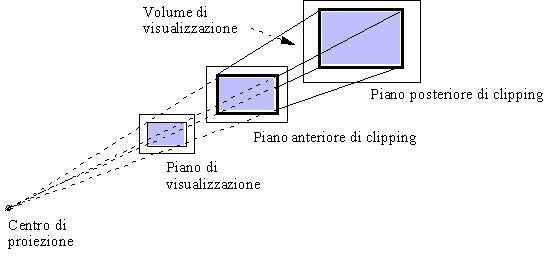 Figura 0.10 Piani
di clipping.
Figura 0.10 Piani
di clipping.
Tenendo presente che occorre prima selezionare il
matrix-mode, la sequenza tipica di comandi è
glMatrixMode(GL_PROJECTION);glLoadIdentity();glFrustum(xmin,
xmax, ymin, ymax, zmin, zmax);
Il piano di clipping anteriore corrisponde al piano z = ñzmin poiché la camera è puntata nella direzione delle coordinate z negative, analogamente il piano posteriore è definito dal piano z = ñzmax.
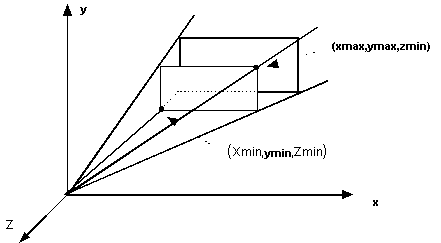 Figura 0.11 Specificazione
del volume di visualizzazione.
Figura 0.11 Specificazione
del volume di visualizzazione.
In molte applicazioni è naturale specificare
líangolo di visualizzazione. Tuttavia, se il piano di proiezione
è rettangolare e non quadrato, abbiamo un angolo di visualizzazione
differente per la vista laterale e per la vista superiore. La
funzione
gluPerspective(fovy, aspect,
near, far)
consente di specificare il campo di visualizzazione nella direzione y e líaspect-ratio (rapporto tra altezza e larghezza) del piano di proiezione. I piani near e far definiscono i due piani di clipping.
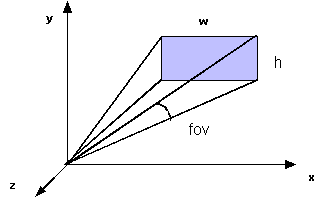 Figura 0.12 Campo
di visualizzazione.
Figura 0.12 Campo
di visualizzazione.
Nel caso di viewing parallelo, la sola funzione resa
disponibile da OpenGL è la funzione
glOrtho(xmin, xmax, ymin, ymax,
zmin, zmax)
che ha gli stessi parametri della funzione glFrustum. Il volume di visualizzazione è in questo caso un parallelepipedo retto, e i piani di clipping anteriore e posteriore sono i piani z = ñzmin e z = ñzmax, rispettivamente.
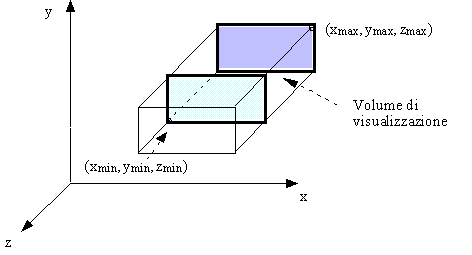 Figura 0.13 Viewing
ortogonale.
Figura 0.13 Viewing
ortogonale.Vogliamo ora definire le proiezioni parallele oblique a partire da quelle ortogonali. Líapproccio che applicheremo è basato su una tecnica chiamata normalizzazione, che consiste nel convertire tutte le proiezioni in proiezioni ortogonali, dopo aver distorto líoggetto da proiettare, in modo tale che la proiezione ortogonale dellíoggetto distorto coincida con la proiezione obliqua desiderata.
Dato che, lavorando in coordinate omogenee la distorsione dellíoggetto può essere descritta in termini di una matrice, la matrice di proiezione complessiva si può ottenere componendo due matrici: la matrice di distorsione e la matrice di proiezione ortogonale.
Nelle proiezioni ortogonali il volume di clipping più semplice con cui trattare è il cubo centrato nellíorigine, le cui facce sono definiti dai sei piani
x = 1
y = 1
z = 1
Possiamo dunque utilizzare la seguente sequenza di
funzioni
glMatrixMode(GL_PROJECTION);glLoadIdentity();glOrtho(-1.0,
1.0, -1.0, 1.0, -1.0, 1.0);
Questo volume è detto volume canonico di
visualizzazione. Supponiamo ora di definire un volume di visualizzazione
differente con il comando
glOrtho(xmin, xmax, ymin, ymax,
zmin, zmax)
La matrice di visualizzazione predisposta da OpenGL
deve dunque convertire i vertici che specificano il nostro oggetto
in vertici allíinterno del volume canonico, scalandoli
e traslandoli in modo tale che i vertici allíinterno del
volume di visualizzazione specificato siano trasformati in vertici
allíinterno del volume canonico, mentre i vertici allíesterno
del volume di visualizzazione siano trasformati in vertici esterni
al volume canonico. In altre parole, la matrice di proiezione
è una matrice 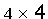
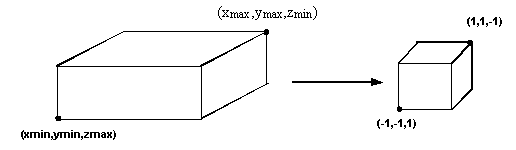 Figura 0.14 Trasformazione
del volume di visualizzazione nel volume canonico.
Figura 0.14 Trasformazione
del volume di visualizzazione nel volume canonico.Per effettuare questa trasformazione dobbiamo eseguire una traslazione per portare il centro del volume di visualizzazione specificato, nel centro del volume canonico (líorigine), seguita da una trasformazione di scala per fare in modo che i lati del volume di visualizzazione abbiano la lunghezza dei lati del volume canonico. Dobbiamo dunque applicare le due trasformazioni
T(ñ(xmax + xmin)/2, ñ(ymax + ymin)/2, ñ(zmax + zmin)/2)
S(2/(xmax ñ xmin), 2/(ymax + ymin), 2/(zmax + zmin))
che concatenate danno luogo alla matrice di proiezione
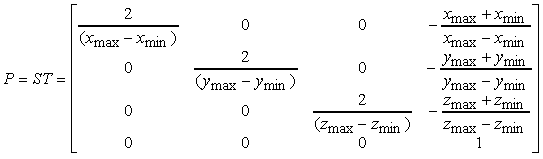
Una strategia analoga a quella appena esaminata può essere utilizzata per definire le proiezioni oblique. In questo caso il volume di visualizzazione è formato da un parallelepipedo non retto, in cui i piani di clipping anteriore e posteriore sono paralleli al piano di proiezione, mentre gli altri piani sono paralleli alla direzione di proiezione.
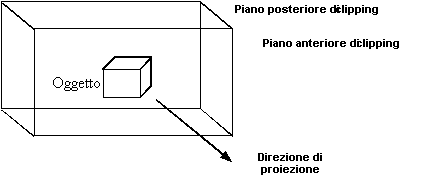 Figura 0.15 Volume
di clipping obliquo.
Figura 0.15 Volume
di clipping obliquo.Le equazioni per le proiezioni oblique si possono derivare considerando i due angoli q e f che caratterizzano la vista superiore e quella laterale, rispettivamente. Se consideriamo la vista superiore, possiamo determinare la coordinata xp notando che
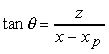
da cui si ottiene
xp = x ñ z cot q.
In modo del tutto analogo, si ricava
yp = y ñ z cot f.
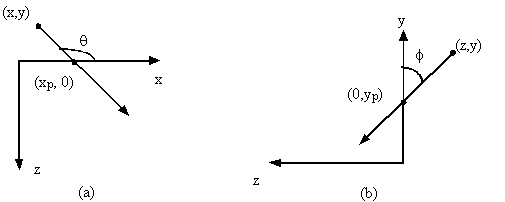 Figura 0.16 (a)
Vista superiore e (b) vista laterale di una proiezione obliqua.
Figura 0.16 (a)
Vista superiore e (b) vista laterale di una proiezione obliqua.Usando líequazione del piano di proiezione zp = 0, possiamo infine scrivere la matrice della trasformazione in coordinate omogenee
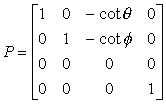
Si osservi che questa matrice può essere scritta come il prodotto tra due matrici: una matrice di proiezione ortogonale e una matrice di deformazione:
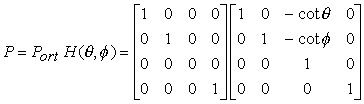
Per completare la proiezione, occorre infine trasformare il volume di visualizzazione nel volume canonico applicando la trasformazione
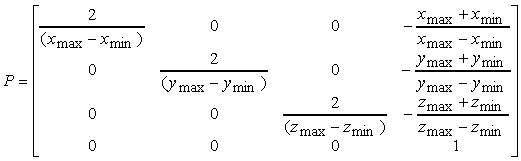
In tre dimensioni, il clipping è effettuato rispetto ad un volume limitato, mentre in due dimensioni il clipping è effettuato rispetto ad una regione limitata nel piano. Líestensione più semplice dal caso bidimensionale al caso tridimensionale si ha nel caso in cui il volume di clipping è un parallelepipedo retto:
xmin x xmax
ymin y ymax
zmin z zmax
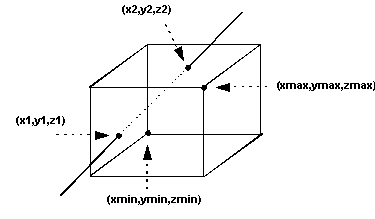 Figura 0.17 Clipping
tridimensionale rispetto ad un parallelepipedo retto.
Figura 0.17 Clipping
tridimensionale rispetto ad un parallelepipedo retto.Gli algoritmi di Cohen-Sutherland, Liang-Barsky e Sutherlabnd-Hodgeman possono essere estesi facilmente al caso tridimensionale.
Nellíalgoritmo di Cohen-Sutherland, líoutcode a 4 bit deve essere sostituito da un codice a 6 bit in cui i due bit addizionali vengono utilizzati per distinguere le due situazioni in cui il punto giace davanti o dietro il volume di clipping.
Nellíalgoritmo di Liang-Barsky, si deve aggiungere líequazione
z(a) = (1 ñ a) z1 + a z2,
per ottenere una rappresentazione parametrica tridimensionale di un segmento lineare, e dovremo quindi considerare sei intersezioni con le superfici che formano il volume di clipping.
La differenza principale tra il clipping bidimensionale e il clipping tridimensionale è data dal fatto che invece di eseguire il clipping di linee contro linee, dobbiamo ora eseguire il clipping sia di linee contro superfici che di superfici contro superfici. Di conseguenza, il calcolo delle intersezioni deve essere modificato.
Il calcolo delle intersezioni può essere posto
in termini di una linea parametrica in tre dimensioni che interseca
un piano. Se scriviamo le equazioni della linea e del piano in
forma matriciale (dove n è la normale al piano e
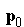
p(a) = (1 ñ a) p1 + a p2
n ï (p(a) ñ p0) = 0
dove a corrisponde al punto di intersezione.
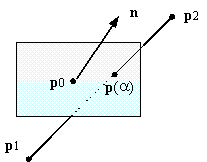 Figura 0.18 Intersezione
linea-piano.
Figura 0.18 Intersezione
linea-piano.La soluzione è data da
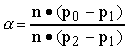
Il calcolo dellíintersezione richiede quindi sei moltiplicazioni ed una divisione. Nel caso delle proiezioni ortogonali, il volume di visualizzazione è un parallelepipedo retto, ed il calcolo di ciascuna intersezione si riduce ad una singola divisione, come nel caso bidimensionale.
Per trattare il caso di volume di visualizzazione obliquo è conveniente applicare la strategia di normalizzazione. Abbiamo visto che una proiezione obliqua è equivalente ad una deformazione seguita da una proiezione ortogonale. La deformazione provoca una distorsione non solo dellíoggetto, ma anche del volume di visualizzazione, in modo da trasformare un parallelepipedo qualsiasi in un parallelepipedo retto.
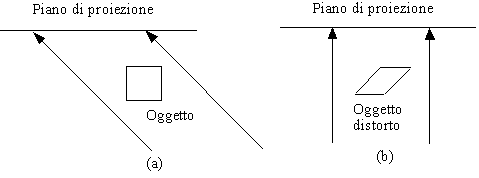 Figura 0.19 Distorsione
del volume di visualizzazione: vista superiore prima (a) e dopo
(b) la distorsione.
Figura 0.19 Distorsione
del volume di visualizzazione: vista superiore prima (a) e dopo
(b) la distorsione.