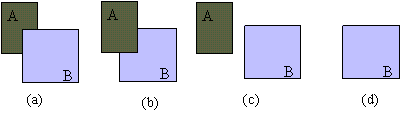
 Figura 5.1 (a)
B oscura parzialmente A; (b) A oscura parzialmente B; (c) A e
B sono completamente visibili; (d) B oscura totalmente A.
Figura 5.1 (a)
B oscura parzialmente A; (b) A oscura parzialmente B; (c) A e
B sono completamente visibili; (d) B oscura totalmente A.Una volta che ad un insieme di vertici sono state applicate le trasformazioni geometriche richieste e gli oggetti definiti da questi vertici sono stati sottoposti al clipping, prima di eseguire la scan conversion, si deve risolvere il problema della rimozione delle superfici nascoste per determinare se un oggetto è visibile allíosservatore, oppure rimane oscurato da altri oggetti della scena.
Gli algoritmi per la rimozione delle superfici nascoste
si possono dividere in due classi:
La libreria OpenGL utilizza un particolare algoritmo, líalgoritmo z-buffer, che appartiene alla seconda classe.
Data una scena tridimensionale composta da k
poligoni piatti ed opachi, si può derivare un generico
algoritmo di tipo object-space considerando gli oggetti a coppie.
Data una coppia di poligoni, ad esempio A e B, ci sono quattro
casi da considerare:
 Figura 5.1 (a)
B oscura parzialmente A; (b) A oscura parzialmente B; (c) A e
B sono completamente visibili; (d) B oscura totalmente A.
Figura 5.1 (a)
B oscura parzialmente A; (b) A oscura parzialmente B; (c) A e
B sono completamente visibili; (d) B oscura totalmente A.Dal punto di vista della complessità, la determinazione del caso da esaminare e il calcolo della parte visibile di un poligono sono considerate come una singola operazione. Si procede quindi induttivamente. Si prende uno dei k poligoni e lo si confronta con tutti i restanti k ñ 1. In questo modo si determina quale parte del poligono sarà visibile. Questo processo è ripetuto con gli altri poligoni. Ad ogni passo si confronta il poligono in esame con tutti i poligoni rimanenti, fino a quando rimangono solo due poligoni. La complessità di questo approccio risulta di ordine O(k2). » dunque chiaro che líapproccio object-space è consigliabile solo quando gli oggetti nella scena sono relativamente pochi.
Líapproccio image-space segue la stessa tecnica adottata per il viewing ed il ray tracing. Per ogni pixel, si considera un raggio che parte dal centro di proiezione e passa per quel pixel. Il raggio è intersecato con ciascuno dei piani determinati dai k poligoni per determinare per quali piani il raggio attraversa un poligono. Infine, si determina quale intersezione è più vicina al centro di proiezione, e si colora il pixel in esame usando la gradazione di colore del poligono nel punto di intersezione.
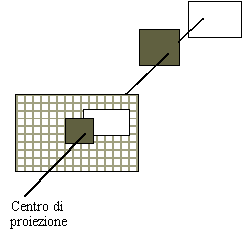 Figura 5.2 Approccio
image-space.
Figura 5.2 Approccio
image-space.Líoperazione fondamentale dellíapproccio image-space è il calcolo delle intersezioni dei raggi con i poligoni. Per un display n ¥ m, questa operazione deve essere eseguita nmk volte, e la complessità risulta di ordine O(k). Naturalmente, per aumentare líaccuratezza delle immagini visualizzate, si possono considerare anche più di un raggio per pixel.
Per ridurre il carico di lavoro richiesto per la rimozione delle superfici nascoste, è opportuno eliminare prima tutti i poligoni il cui vettore normale è orientato verso il semispazio opposto allíosservatore, ossia i poligoni che definiscono la parte posteriore della superficie di un oggetto solido, non visibile allíosservatore.
Per determinare se un poligono deve essere eliminato, dobbiamo verificare se la sua normale è diretta o meno verso líosservatore. Se indichiamo con q líangolo tra la normale e líosservatore, il poligono in esame definisce la parte anteriore di un oggetto se e solo se
-90° £ q £ 90°,
o, equivalentemente
cos q 0.
La seconda condizione è più facile da controllare, poiché, invece di calcolare il coseno, possiamo valutare il prodotto scalare
n ï v 0.
In OpenGL, líeliminazione delle back faces viene eseguita dalla funzione glCullFace.
Líalgoritmo z-buffer è un algoritmo di tipo image-space, basato su una logica molto semplice, e facile da implementare. Esso lavora in stretto accoppiamento con líalgoritmo di scan conversion, e necessita, oltre alla memoria di display (frame buffer), anche di uníarea di memoria in cui memorizzare le informazioni di profondità relative ad ogni pixel. Questíarea addizionale di memoria è chiamata z-buffer.
Nonostante líalgoritmo z-buffer sia di tipo image-space, i cicli al suo interno sono eseguiti rispetto ai poligoni e non rispetto ai pixel.
Supponiamo di dovere visualizzare due poligoni. Nel corso dellíesecuzione della scan conversion, è possibile calcolare il colore da associare ad ogni punto di intersezione tra un raggio diretto dal centro di proiezione ad un pixel, applicando un modello di shading. Contemporaneamente, si può anche controllare se il punto di intersezione è visibile o meno, secondo la regola che stabilisce che il punto è visibile se è il punto di intersezione più vicino al centro di proiezione. Quindi, se si esegue la scan conversion del poligono B, il suo colore apparirà sullo schermo poiché la distanza z1 è minore della distanza z2 relativa al poligono A (si veda la figura 5.3). Al contrario, se si esegue la scan conversion del poligono A, il pixel che corrisponde al punto di intersezione non apparirà sul display.
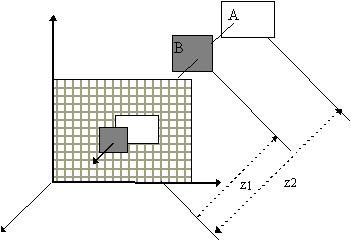 Figura 5.3 Líalgoritmo
z-buffer.
Figura 5.3 Líalgoritmo
z-buffer.Poiché si procede poligono per poligono, non è possibile disporre di tutte le informazioni relative agli altri poligoni. Tuttavia, si possono memorizzare e aggiornare le informazioni relative alla profondità che si rendono via via disponibili, nel corso della scan conversion.
Supponiamo di avere a disposizione una memoria, lo z-buffer, con la stessa risoluzione del frame buffer e con una profondità consistente con la risoluzione che si vuole ottenere per le distanze. Ad esempio, se abbiamo un display 1024 ¥ 1280 e utilizziamo líaritmetica in virgola mobile per i calcoli di profondità, possiamo utilizzare uno z-buffer 1024 ¥ 1280, con elementi a 32 bit. Ogni elemento è inizializzato al valore della distanza massima dal centro di proiezione. Il frame buffer è inizializzato al colore di sfondo. Ad ogni istante, nel corso della scan conversion, ogni locazione dello z-buffer contiene la distanza, lungo il raggio corrispondente a quella locazione, del punto di intersezione più vicino tra quelli relativi a tutti i poligoni incontrati fino a quel momento.
La computazione procede nel modo seguente. Si effettua la scan conversion, poligono per poligono. Per ciascun punto sul poligono che corrisponde allíintersezione del poligono con un raggio che passa attraverso un pixel, si calcola la distanza del punto dal centro di proiezione, e la si confronta con il valore memorizzato nello z-buffer, in corrispondenza a quel pixel. Se la distanza è maggiore della distanza memorizzata nello z-buffer, significa che abbiamo già incontrato un poligono più vicino allíosservatore, e il punto in esame non sarà quindi visibile. Se invece la distanza è minore di quella presente nello z-buffer, significa che abbiamo individuato un poligono più vicino allíosservatore, e dobbiamo quindi aggiornare la distanza nello z-buffer e memorizzare il colore calcolato per il punto in esame nella locazione corrispondente nel frame buffer.
Uno dei principali vantaggi dellíalgoritmo z-buffer è la sua semplicità. Inoltre, esso si inserisce molto bene nellíapproccio object-oriented delle implementazioni poiché il carico di lavoro incrementale è limitato. Supponiamo di eseguire la scan conversion di un poligono, linea di scansione per linea di scansione. Il poligono appartiene ad un piano che può essere rappresentato dallíequazione
a x + b y + c z + d = 0.
Supponiamo che (x1, y1, z1) e (x2, y2, z2) siano due punti sul poligono. Se
Dx = x2 ñ x1,
Dy = y2 ñ y1,
Dz = z2 ñ z1,
líequazione del piano può essere scritta in forma incrementale:
a x + b y + c z + d = 0.
Ogni linea di scansione corrisponde ad una linea di ordinata y costante, quindi Dy = 0 quando ci si muove su una linea di scansione. Líincremento Dx della coordinata x ad ogni passo è costante, e corrisponde allo spostamento da un pixel a quello successivo nel frame buffer. Quindi, quando ci si muove da un punto allíaltro lungo una linea di scansione risulta
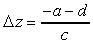
e questo valore è una costante che deve essere calcolata una sola volta per ciascun poligono.
Líalgoritmo depth sort (di ordinamento in profondità) è una implementazione dellíapproccio object-space.
Consideriamo una scena composta da poligoni planari (estensioni a casi più complessi sono possibili). Líalgoritmo depth sort è una variante di un algoritmo ancora più semplice, chiamato algoritmo del pittore. Supponiamo che i poligoni siano ordinati sulla base della loro distanza dallíosservatore. Per rappresentare correttamente la scena, potremmo individuare la parte visibile del poligono più distante, e predisporla nel frame buffer. Se i poligoni sono solo due, questa operazione richiede líesecuzione del clipping di un poligono rispetto allíaltro. Uníaltra possibilità è invece quella di seguire un approccio analogo a quello usato da un pittore: dipingere prima il poligono più lontano interamente, e poi dipingere il poligono più vicino, dipingendo sopra le parti del poligono più lontano non visibili allíosservatore. Líidea alla base dellíalgoritmo depth sort è proprio quella di visualizzare gli elementi in modo inverso rispetto allíordine di profondità. In questo modo gli elementi più lontani sono progressivamente oscurati da quelli più vicini allíosservatore.
I problemi da risolvere per implementare questo approccio riguardano líordinamento in profondità dei poligoni, e la situazione di sovrapposizione tra poligoni.
Supponiamo di avere già calcolato líestensione di ogni poligono. Il passo successivo dellíalgoritmo depth sort riguarda líordinamento dei poligoni in base alla distanza della loro coordinata z massima dallíosservatore. Più precisamente, si considera líestensione nella direzione z di ogni poligono (si veda la figura 5.4).
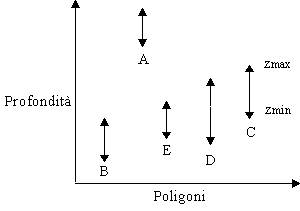 Figura 5.4 Estensioni
z dei poligoni.
Figura 5.4 Estensioni
z dei poligoni.Se la profondità minima di ogni poligono è maggiore della profondità massima del poligono situato sul retro, possiamo dipingere i poligoni partendo da quello più in profondità (è il caso del poligono A nellíesempio in figura, che è situato dietro a tutti gli altri poligoni e può essere dipinto per primo). Gli altri poligoni, tuttavia, non possono essere dipinti basandosi solo sulla loro estensione lungo z. Se le estensioni z di due poligoni si sovrappongono, dobbiamo determinare un ordine per dipingerli individualmente che permetta di ottenere líimmagine corretta. Líalgoritmo depth sort esegue a questo scopo una serie di test. Consideriamo ad esempio una coppia di poligoni le cui estensioni z si sovrappongono. Il test più semplice consiste nel controllare le estensioni lungo x e lungo y. Se non cíè sovrapposizione in almeno una delle due direzioni, allora sicuramente nessuno dei due poligoni può oscurare líaltro, ed essi possono essere dipinti in un ordine qualsiasi.
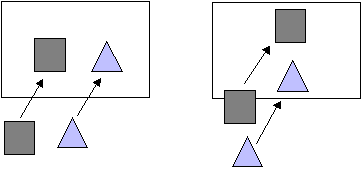 Figura 5.5 Test
di sovrapposizione delle estensioni x e y.
Figura 5.5 Test
di sovrapposizione delle estensioni x e y.Se questo test fallisce, può essere ancora possibile trovare un ordine corretto per dipingere i poligoni, ad esempio se tutti i vertici di un poligono cadono dalla stessa parte del piano determinato dallíaltro poligono.
Rimangono da considerare due situazioni problematiche, per cui non esiste un ordine corretto di rappresentazione. La prima si verifica quando tre o più poligoni si sovrappongono ciclicamente. La seconda situazione si verifica invece quando un poligono penetra nellíaltro.
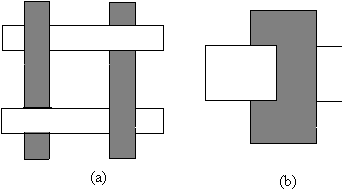 Figura 5.6 (a)
Sovrapposizione ciclica. (b) Compenetrazione di poligoni.
Figura 5.6 (a)
Sovrapposizione ciclica. (b) Compenetrazione di poligoni.In questi casi, è necessario derivare i dettagli delle intersezioni, spezzare i poligoni in corrispondenza dei segmenti di intersezione, e provare a cercare un ordine corretto di rappresentazione del nuovo insieme di poligoni.
Líanalisi delle prestazioni dellíalgoritmo depth sort è difficile poiché i particolari delle singole applicazioni determinano quanto spesso si possano verificare i casi difficili da trattare. In ogni caso, la complessità risulta più che lineare nel numero di poligoni, poiché è necessario eseguire un algoritmo di sorting delle profondità.
Líalgoritmo scan line combina scan conversion di poligoni e rimozione delle superfici nascoste.
Per descrivere gli aspetti salienti dellíalgoritmo consideriamo la figura 5.7, che mostra due poligoni che si intersecano, e due linee di scansione.
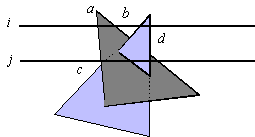 Figura 5.7 Algoritmo
scan line.
Figura 5.7 Algoritmo
scan line.Se ci si muove da sinistra verso destra lungo la linea i, si incrocia il lato a del poligono A, e si entra così nel primo poligono. In questo caso, non è necessario eseguire alcun calcolo di profondità: nessun altro poligono può influenzare il colore lungo questa linea. Quando si incrocia il lato successivo, b, si esce dal poligono A, e si può colorare il pixel corrispondente usando il colore di sfondo. Quindi, si incontra il lato c del poligono B; anche in questo caso, avendo un solo poligono da considerare, si possono evitare i calcoli di profondità. La linea di scansione j mostra una situazione ben più complessa. Prima si incrocia il lato a, e si può assegnare un colore evitando i calcoli di profondità. Il secondo lato che si incrocia è invece c. Ciò significa che i due poligoni sono sovrapposti e si devono quindi eseguire i calcoli di profondità, fino a quando non si oltrepassa il lato d.
Questa strategia ha degli elementi in comune con líalgoritmo z-buffer, ma è allo stesso tempo completamente diversa poiché lavora con una linea di scansione alla volta e non con un poligono alla volta.
Nei sistemi grafici moderni, un programma utente non puÚ scrivere e leggere dai buffer.
» importante avere il supporto hardware e sfoftware
per un insieme di operazioni che operano su blocchi rettanglari
di pixel, conosciute con il nome di bit-block transfer
(bitblt).
WriteBlock(source, x, y, w, h, destination, u, v);
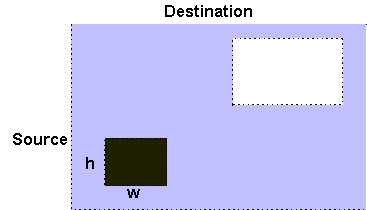 Figura 5.8 RasterOP
Figura 5.8 RasterOP
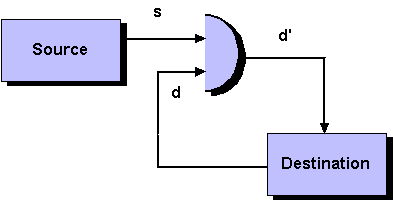 Figura 5.9 Writing
modes.
Figura 5.9 Writing
modes.
d f(d,
s)
 Fig. 5. Modalit‡
OR e XOR.
Fig. 5. Modalit‡
OR e XOR.