1. ALGORITMI E PRIMITIVE PER LA GRAFICA RASTER BIDIMENSIONALE
2. Stadi principali

La visualizzazione di un modello grafico passa attraverso quattro stadi principali, che costituiscono la cosiddetta pipeline grafica:

1. Modellazione
2. Elaborazione geometrica
3. Rasterizzazione
4. Display

Figura 4.1 Pipeline grafica.

Il risultato della modellazione è un insieme di vertici che specificano un insieme di oggetti geometrici gestiti dal sistema grafico.

Il compito dell'elaborazione geometrica è quello di determinare quali oggetti appaiono sullo schermo e di assegnare colori e ombre a tali oggetti. Quattro procedimenti vengono applicati: normalizzazione, clipping, rimozione delle linee nascoste ed ombreggiatura.

Dopo che è stata effettuata la proiezione, si lavora con oggetti bidimensionali. Si ha ad esempio un insieme di vertici degli oggetti da visualizzare. Per visualizzare tali oggetti, occorre usare questi vertici per generare un insieme di pixel, tramite un processo di rasterizzazione o scan conversion.

Infine, il processo di trasferimento dell'immagine dal frame-buffer allo schermo è svolto automaticamente dall'hardware grafico.

1. Strategie di Implementazione

Nei sistemi di grafica raster le primitive geometriche, descritte in termini dei loro vertici sul piano cartesiano, sono approssimate da matrici di pixel. Con una matrice abbastanza densa è possibile rappresentare praticamente qualsiasi oggetto geometrico, anche complesso: punti, linee, cerchi, ellissi, etc. La procedura con cui le figure di tipo continuo si rappresentano come insieme di pixel discreti è chiamata scan conversion (conversione di scansione).

Un'altra operazione fondamentale per passare dalla definizione geometrica di una primitiva nel programma applicativo alla sua visualizzazione sul dispositivo di output grafico è il clipping, ovvero il processo che consiste nell'eliminazione delle parti degli oggetti al di fuori della regione di visualizzazione. Ci sono diversi modi per effettuare il clipping. La tecnica più ovvia è quella di effettuare il clipping della primitiva prima della scan conversion, calcolandone le intersezioni analitiche con i bordi del rettangolo di visualizzazione; i punti di intersezione sono quindi usati per definire nuovi vertici per la primitiva. Il vantaggio di eseguire il clipping prima della scan conversion risiede ovviamente nel fatto che la scan conversion deve trattare solo con la nuova versione delle primitive, non con quella originale, che potrebbe essere molto più estesa. Questa tecnica è usata molto spesso per il clipping di segmenti, rettangoli e poligoni per i quali gli algoritmi di clipping risultano piuttosto semplici ed efficienti. Una tecnica più semplice per il clipping è lo scissoring, che consiste nell'effettuare la scan conversion dell'intera primitiva e nella visualizzazione solo dei pixel all'interno del rettangolo di visualizzazione. In linea di principio, questa procedura confronta le coordinate di ciascun pixel con le coordinate (x, y) dei bordi del rettangolo di visualizzazione, prima di scrivere il pixel. In pratica, si cerca di ottimizzare il procedimento, evitando di controllare, ad esempio, i pixel adiacenti sulla stessa linea di scansione.

I display raster invocano gli algoritmi di clipping e scan conversion ogni volta che un'immagine viene creata o modificata. Questi algoritmi non solo devono creare immagini visualizzabili in modo soddisfacente, ma devono eseguire queste operazioni il più velocemente possibile. Come vedremo, gli algoritmi di scan conversion usano metodi incrementali per minimizzare il numero di calcoli da eseguire durante ogni iterazione; inoltre essi usano l'aritmetica intera e non quella in virgola mobile.

Ci sono due approcci fondamentali per realizzare le implementazioni grafiche. Ciascuno deve naturalmente eseguire gli incarichi fondamentali sopra specificati, la differenza tra i due approcci sta nell'ordine in cui gli incarichi sono eseguiti. Possiamo pensare alle differenze tra i due approcci, concettualmente, in termini di un singolo programma che esegue l'implementazione. Il programma prende in input un insieme di vertici che specificano gli oggetti geometrici e produce in output i pixel nel frame buffer. Per produrre un'immagine il programma deve considerare ciascun pixel, e per produrre un'immagine corretta, deve processare ogni primitiva geometrica e ogni sorgente luminosa. Quindi ci aspettiamo che il programma contenga dei loop iterati su questa variabile di base.

Per scrivere un tale programma, dobbiamo quindi stabilire con quale variabile controllare il loop principale del programma, e in base a questa scelta determiniamo il flusso dell'intero processo di implementazione.

Le due strategie sono chiamate image-oriented e object-oriented.

Nell'approccio object-oriented il programma è controllato da un ciclo della forma
for (each_object) render(object);

I vertici sono definiti dal programma e sono sottoposti ad una serie di moduli che li trasformano, li colorano e determinano se sono visibili.

La maggiore limitazione dell'approccio object-oriented è il grosso ammontare di memoria richiesto e l'alto costo dovuto al fatto di processare ciascun oggetto indipendentemente. Ogni primitiva geometrica che emerge dal processing geometrico potenzialmente può influenzare ciascun insieme di pixel nel frame buffer; quindi l'intero frame buffer deve essere della dimensione del display e deve essere disponibile ad ogni istante. Solo recentemente, grazie al fatto che le memorie sono diventate più dense e più economiche, queste richieste sono diventate accettabili.

L'approccio image-oriented è invece basato su un ciclo esterno della forma
for (each_pixel) assign_a_color(pixel);

Per ogni pixel (o linea di scansione) si lavora backward, cercando di determinare quali primitive geometriche possono contribuire alla sua colorazione. Il vantaggio di un tale approccio è che abbiamo bisogno solo di uno spazio di memoria di display limitato ad ogni passo, e che possiamo sperare di generare pixel (o linee di scansione) alla frequenza e nell'ordine richieste per il refresh del display. Dato che i risultati della maggior parte di calcoli non differiscono significativamente da pixel a pixel (o da linea di scansione a linea di scansione) possiamo usare questa coerenza negli algoritmi sviluppando tecniche incrementali per molti dei passi dell'implementazione. Il maggiore svantaggio di questo approccio è che, a meno che costruiamo prima una opportuna struttura di dati geometrici, non sappiamo quali primitive influenzeranno quali pixel. Una tale struttura dati può essere molto complessa e può implicare che tutti i dati geometrici debbano essere disponibili ad ogni passo del processo di rendering. Nel seguito propenderemo per l'approccio object-oriented.

1. Scan Conversion dei segmenti

In questa sezione descriveremo alcuni algoritmi per la scan conversion dei segmenti. Faremo l'ipotesi di aver già effettuato il clipping delle primitive, e supporremo che gli oggetti siano già stati proiettati sul piano bidimensionale. Trascureremo inoltre l'effetto della rimozione di linee nascoste, su cui torneremo più avanti.

Supponiamo che il frame buffer sia una matrice n  m di pixel, con origine nell'angolo in basso a sinistra. I pixel possono essere accesi attraverso una singola istruzione all'interno dell'implementazione grafica della forma
writePixel(int x, int y, int color);

L'argomento value può essere un indice, nei sistemi basati su tabelle, oppure può corrispondere al valore di un pixel, rappresentato ad esempio da un numero a 32 bit, come nel sistema di colorazione RGBA. Il frame buffer è inerentemente discreto, per questo motivo possiamo usare i numeri interi per individuare le locazioni dei pixel al suo interno. Al contrario, le coordinate sullo schermo sono rappresentate da numeri reali.

I pixel possono essere visualizzati secondo diverse forme e dimensioni. Per il momento supponiamo che ciascuno sia visualizzato come un quadrato centrato nella locazione associata al pixel stesso, e di lato pari alla distanza tra due pixel. Infine, faremo l'ipotesi che un processo concorrente legga il contenuto del frame buffer e visualizzi l'immagine sul display alla frequenza desiderata. Questa assunzione ci permette di trattare la scan conversion indipendentemente dalla visualizzazione del contenuto del frame buffer.

1. L'algoritmo DDA

Supponiamo di avere un segmento lineare definito dagli estremi (x₁, y₁) e (x₂, y₂). Assumeremo che questi valori siano già stati arrotondati in modo da corrispondere esattamente alla locazione di due pixel. Si osservi che questa assunzione non è necessaria per derivare l'algoritmo. Infatti, si può utilizzare una rappresentazione in virgola mobile per gli estremi e fare i calcoli usando l'aritmetica in virgola mobile, con il vantaggio di ottenere una scan conversion più accurata.

La pendenza del segmento è definita da

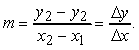
Il più semplice algoritmo di scan conversion per i segmenti lineari consiste nel calcolare m, incrementare x di 1 a partire dal punto più a sinistra e nel calcolare y_i = mx_i + h, dove h è l'ordinata del punto dove la retta incrocia l'asse y, per ciascuno degli x_i.

Questa strategia è tuttavia inefficiente, perché ciascuna iterazione richiede una moltiplicazione ed una somma in virgola mobile ed un arrotondamento mediante l'invocazione di round(). Si può eliminare la moltiplicazione usando una tecnica incrementale, che consiste nel calcolare un punto della retta sulla base del punto precedente. L'algoritmo che si ottiene prende il nome di algoritmo DDA (dall'inglese digital differential analyzer). Il DDA è un dispositivo meccanico che risolve le equazioni differenziali applicando un metodo numerico. Dato che una retta di pendenza m soddisfa l'equazione differenziale

,

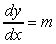
generare un segmento è equivalente a risolvere numericamente una semplice equazione differenziale.

Assumiamo che 0  m  1, gli altri valori di m possono essere trattati in modo simmetrico. L'algoritmo DDA consiste nel tracciare un pixel per ciascun valore di x compreso tra x₁ e x₂, tramite il comando writePixel(). Per ogni variazione di x pari a Dx, la corrispondente variazione di y deve essere pari a Dy = m Dx. Muovendosi da x₁ a x₂, x viene incrementato di 1 ad ogni iterazione, ossia Dx  = 1, e dunque dobbiamo incrementare y di Dy = m.

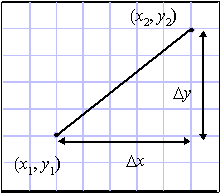Figura 4.2 Segmento di linea.

Nonostante ciascun x sia un numero intero, ciò non vale per y poiché m è un numero in virgola mobile. È dunque necessario arrotondare y ad un valore intero, mediante la funzione round(), per determinare il pixel appropriato.

L'algoritmo risultante è il seguente:
int x;float dy, dx, y, m;dy = y2 - y1;dx = x2 - x1;m = dy/ dx;y = y1;for (x = x1, x <= x2, x++){ writePixel(x, round(y), line_color); y += m;}

Figura 4.3 Pixel visualizzati dall'algoritmo DDA.

La ragione per cui abbiamo limitato la pendenza massima a 1 può essere compresa osservando la figura 4.3.

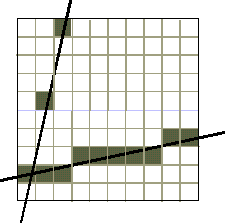Figura 4.4 Pixel generati per segmenti di alta e bassa pendenza.

L'algoritmo DDA è infatti della forma: per ogni x, cerca il miglior y, e per pendenze notevoli, la separazione tra i pixel accesi per rappresentare il segmento, può risultare notevole e generare un'approssimazione inaccettabile. Per pendenze maggiori di 1, possiamo allora scambiare x e y, in modo tale che l'algoritmo diventi della forma: per ogni y, cerca il miglior x.

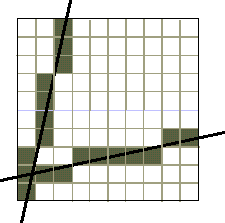Figura 4.5 Pixel generati dall'algoritmo DDA modificato.

Dato che i segmenti di linea sono determinati dai vertici, possiamo usare l'interpolazione per assegnare colori differenti ad ogni pixel generato. Possiamo inoltre ottenere pattern punteggiati o tratteggiati, cambiando alternativamente il colore usato per generare i pixel. In ogni caso, questi dettagli non sono direttamente collegati agli algoritmi di scan conversion, che hanno come compito fondamentale solo quello di determinare i pixel da accendere.

1. L'algoritmo di Bresenham

L'algoritmo DDA è abbastanza efficiente e può essere facilmente implementato. Tuttavia esso richiede un'addizione in virgola mobile per ogni pixel generato. L'algoritmo di Bresenham per la scan conversion delle rette evita invece i calcoli in virgola mobile, e per questo motivo è diventato un algoritmo standard.

Supponiamo, esattamente come nell'algoritmo DDA, che il segmento lineare abbia estremi nei punti di coordinate (x₁, y₁) e (x₂, y₂) e che la pendenza m sia compresa tra 0 e 1.

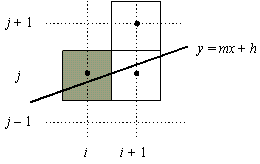Figura 4.6 Condizioni richieste dall'algoritmo di Bresenham.

Supponiamo di essere ad un passo intermedio del procedimento di scan conversion del segmento, e di aver acceso il pixel in posizione (i, j). Per x = i la retta y = mx + h, a cui appartiene il segmento, deve passare attraverso il pixel centrato su (i, j) (stiamo assumendo che i centri dei pixel siano posti nei punti intermedi tra due interi); infatti, in caso contrario, l'operazione di arrotondamento non avrebbe generato questo pixel. Se andiamo avanti a x = i + 1, la condizione sulla pendenza indica che dobbiamo accendere uno tra due pixel possibili: o il pixel in posizione (i + 1, j) o il pixel in posizione (i + 1, j + 1). Avendo ridotto la nostra scelta a soli due pixel, possiamo riformulare il problema in termini di una variabile decisionale d = b - a, dove a e b rappresentano le distanze tra la retta e i due pixel candidati, di ascissa x = i + 1, e di ordinata y = j + 1 e y = j, rispettivamente (si veda la figura 4.6).

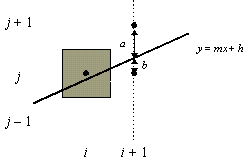Figura 4.7 Variabile di decisione dell'algoritmo di Bresenham.

Se la variabile di decisione ha valore negativo, la retta passa più vicino al pixel più in basso, così la scelta migliore, che garantisce la migliore approssimazione per il segmento, è quella rappresentata dal pixel in posizione (i + 1, j); altrimenti, sceglieremo il pixel in posizione (i + 1, j + 1). Si potrebbe calcolare d usando y = mx + h, ma questo richiede calcoli in virgola mobile.

Per ottenere il vantaggio computazionale dell'algoritmo di Bresenham, occorrono due ulteriori passi. Per prima cosa usiamo una tecnica incrementale per calcolare d, e quindi eliminiamo i calcoli in virgola mobile.

Supponiamo che d_i sia il valore assunto da d in corrispondenza di x = i. Vogliamo calcolare d_i+1 incrementalmente, a partire da d_i. Ci sono due situazioni da considerare, che dipendono dal fatto che al passo precedente sia stata incrementata, o meno, la locazione y del pixel (figura 4.7).

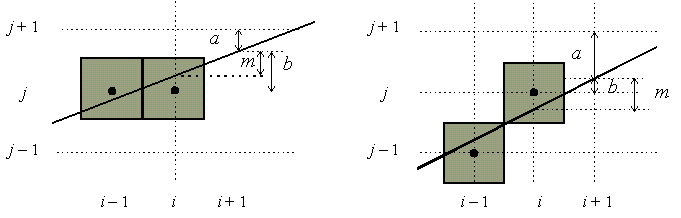Figura 4.8 Incremento dei valori di a e b.

Osserviamo che a, che è pari alla distanza tra la locazione del pixel con ordinata maggiore e la retta, diminuirà di un fattore m se y non era stata incrementata dalla decisione precedente; altrimenti aumenterà di un fattore 1-m. Analogamente, b cresce di un fattore m, o aumenta di un fattore m-1 quando incrementiamo y. Quindi le variazioni di (b - a) sono 2m oppure 2 - 2m.

Possiamo eliminare i calcoli in virgola mobile osservando che ci interessa solo il segno di d, e quindi possiamo moltiplicare d per Dx, senza influenzare il risultato. In tal modo le possibili variazioni di d sono pari a 2Dy oppure a 2(Dy - Dx). Possiamo esprimere questo risultato nella forma seguente

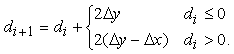
Il calcolo di ogni pixel successivo richiede dunque solo un'addizione e un test di segno.

Riassumendo, ad ogni passo l'algoritmo sceglie tra due pixel sulla base del segno della variabile di decisione calcolata nell'iterazione precedente, quindi aggiorna la variabile a seconda del pixel che è stato scelto.
dx = x2 - x1;dy = y2 - y1;d = dy * 2 - dx;incrE = 2 * dy;incrNE = 2 * (dy - dx);x = x1;y = y1;writePixel(x, y, value);while (x < x2) { if (d <= 0 { d += incrE; x++; } else { d += incrNE; x++; y++; } writePixel(x, y, value);}

Si osservi che il primo pixel è dato dall'estremo (x₁, y₁) del segmento, da cui possiamo calcolare direttamente il valore iniziale della variabile di decisione. Si osservi inoltre che l'algoritmo richiede solo l'esecuzione di addizioni, sottrazioni e moltiplicazioni per due di numeri interi, operazioni eseguibili velocemente dal calcolatore. Tale algoritmo è così efficiente che è stato incorporato come singola istruzione nei chip grafici.

1. Scan Conversion del cerchio

Sebbene il cerchio non sia tra le primitive di OpenGL, vediamo comunque come sia possibile ottenere la scan conversion di questa figura geometrica.

Per prima cosa, osserviamo che, essendo il cerchio una figura simmetrica, di questa simmetria può trarre vantaggio l'algoritmo che lo genera, tracciando otto punti per ogni valore calcolato. Dato un punto sul cerchio di coordinate (x, y), gli altri sette si trovano riflettendo, scambiando e invertendo di segno le coordinate:

P₁ = (x, y) P₅ = (-x, -y)

P₂ = (y, x) P₆ = (-y, -x)

P₃ = (-y, x) P₇ = (y, -x)

P₄ = (-x, y) P₈ = (x, -y)

Quindi potremo usare la seguente funzione ausiliaria:
void CirclePoints(float x, float y, int color){writePixel(x, y, color);writePixel(y, x, color);writePixel(-y, x, color);writePixel(-x, y, color);writePixel(-x, -y, color);writePixel(-y, -x, color);writePixel(y, -x, color);writePixel(x, -y, color);}

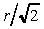
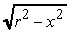
Per la definizione matematica del cerchio con centro nell'origine abbiamo due metodi standard. Il primo consiste nell'equazione di secondo grado y² = r² - x², dove r rappresenta il raggio. Le coordinate x del settore compreso tra 90° e 45° si trovano percorrendo le ascisse da 0 a ; le y si trovano calcolando di volta in volta . Tuttavia, questo è un metodo poco efficiente: per ogni punto bisogna calcolare il quadrato di r e di x, fare una sottrazione e quindi estrarre la radice quadrata.

Un secondo metodo per definire il cerchio fa uso delle funzioni trigonometriche x = r cos , y = r sin 

Si fa variare l'angolo per passi, tra 0 e /4, e in corrispondenza a ciascun valore di vengono calcolati i valori di x e y. Ma anche il calcolo delle funzioni trigonometriche risulta computazionalmente pesante.

Per ottenere un tratteggio efficiente del cerchio conviene evitare sia elevamenti a potenza che calcoli trigonometrici. Come nel caso dei segmenti, è desiderabile eseguire i calcoli che consentono di individuare i pixel da visualizzare ricorrendo solo ad addizioni, sottrazioni e moltiplicazioni per potenze di due dei numeri interi. Anche in questo caso si può applicare in modo efficace l'algoritmo di Bresenham.

La conversione del cerchio con questo algoritmo è basata sull'ottuplice simmetria, per cui è sufficiente generare i punti di un settore circolare di 45°, procedendo dai 90° ai 45°. L'approssimazione migliore al cerchio è data dai pixel a minore distanza da esso. Ad ogni passo, il pixel più prossimo al cerchio si può ottenere in due diversi modi: (1) spostandosi di una unità sulle x oppure (2) spostandosi di una unità sulle x e di una sulle y negative. Si deve quindi effettuare una scelta tra queste due possibilità.

Supponiamo che l'ultimo pixel individuato sia P. Indichiamo con D(E) la differenza tra il quadrato della distanza tra un punto del cerchio vero e l'origine e il quadrato della distanza tra l'origine e il punto E (figura 4.8). Sia inoltre D(SE) la differenza tra i quadrati delle distanze tra punto del cerchio vero e l'origine e tra l'origine e il punto SE.

Le uniche mosse possibili sono avanzare di un passo lungo le x, oppure avanzare di un passo sulle x e di uno sulle y negative, pertanto deve valere una delle due espressioni

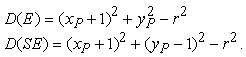
Poiché D(E) sarà sempre positiva e D(SE) sempre negativa, si può definire una variabile di decisione d:

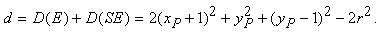
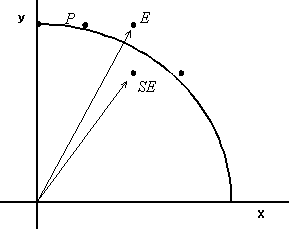Figura 4.9 Scan conversion del cerchio.

Tenendo presente che il centro del cerchio è nell'origine, al primo passaggio avremo x = 0 e y = r, quindi risulta d₁ = 3 - 2r. Quando d_i > 0, incrementiamo solo la x:

x_i+1 = x_i + 1

d_i+1 = d_i + 4x_i + 6

mentre se risulta d_i  0, incrementiamo anche la y:

x_i+1 = x_i + 1

y_i+1 = y_i - 1

d_i+1 = d_i + 4 (x_i - y_i) + 10.

L'algoritmo risultante è il seguente:
int x, y;float d;x = 0; /* inizializzazione */y = radius;d = 5.0 / 4 - radius;CirclePoints(x, y, line_color);while (y > x) {if (d < 0) { /* scelta di E */d += x * 2.0 + 3;x++;} else { /* scelta di SE */d += (x - y) * 2.0 + 5;x++;y--;}CirclePoints(x, y, line_color);}

L'algoritmo risultante è il seguente:
int x, y, deltaE, deltaSE;x = 0; /* inizializzazione */y = radius;d = 1 - radius;deltaE = 3;deltaSE = 5 - radius * 2;CirclePoints(x, y, line_color);while (y > x) {if (d < 0) { /* scelta di E */d += deltaE;deltaE += 2;deltaSE += 2;x++;} else { /* scelta di SE */d += deltaSE;deltaE += 2;deltaSE += 4;x++;y--;}CirclePoints(x, y, line_color);}

1. Scan Conversion dei poligoni

Uno dei principali vantaggi introdotti dalla grafica raster è stato quello di permettere il riempimento delle aree interne dei poligoni. Il termine rasterizzazione (o scan conversion) dei poligoni è diventato così sinonimo del concetto di riempimento di un poligono con un singolo colore. A differenza della scan conversion dei segmenti, dove un singolo algoritmo ha un ruolo dominante sugli altri, per i poligoni sono stati sviluppati e applicati diversi metodi, e la scelta di un metodo in particolare dipende fortemente dall'architettura su cui si effettua l'implementazione.

Supponiamo di voler riempire il poligono con un unico colore (scelta che ci consente di semplificare la trattazione). La regola di base per effettuare il riempimento del poligono è la seguente: se un punto è all'interno del poligono, coloralo usando il colore di riempimento prescelto. Questo algoritmo concettuale mostra come il problema di riempimento di un poligono sia in effetti un problema di ordinamento, basato sulla divisione dei pixel del frame buffer in due categorie: quelli che sono all'interno del poligono e quelli che sono all'esterno. Da questo punto di vista, si ottengono algoritmi di riempimento differenti a seconda della tecnica con cui i pixel sono ordinati nei due gruppi.

1. Flood fill

Possiamo visualizzare un poligono solo tramite i suoi lati, senza colorare la regione interna, applicando l'algoritmo di Bresenham per effettuare la scan conversion dei lati. Supponiamo di avere solo due colori a disposizione: un colore di sfondo (bianco) e un colore di primo piano, o di drawing (grigio). Possiamo usare il colore di drawing per la scan conversion dei lati ottenendo, ad esempio, il frame buffer illustrato in figura 4.9.

Per effettuare il riempimento del poligono possiamo poi operare nel modo seguente. Se possiamo individuare un punto iniziale di coordinate (x, y) all'interno del poligono, allora consideriamo ricorsivamente i punti vicini, e li coloriamo di grigio se non appartengono ai lati del poligono. L'algoritmo può essere espresso nel seguente modo, in cui assumiamo che ci sia una funzione readPixel che restituisce il colore di un pixel:
floodFill(int x, int y){if (readPixel(x, y) == WHITE){writePixel(x, y, GRAY);floodFill(x-1, y);floodFill(x+1, y);floodFill(x, y-1);floodFill(x, y+1);}}

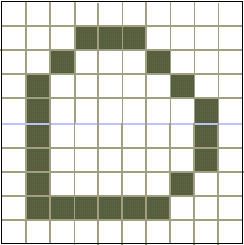Figura 4.10 Poligono visualizzato tramite i suoi lati.

Dell'algoritmo si possono ottenere diverse varianti, ad esempio rimuovendo la ricorsione. Il lettore può sviluppare un algoritmo del genere come esercizio.

1. Algoritmo Scan-lineAlgoritmo Scan-line

L'algoritmo di scan conversion dei poligoni basato sull'uso delle linee di scansione consente di trattare qualsiasi tipo di poligono, anche quelli che hanno dei buchi all'interno. L'algoritmo scan-line calcola per prima cosa i gruppi di pixel - gli span - che giacciono tra i lati a sinistra e a destra del poligono.

Si consideri ad esempio il poligono in figura 4.10. Se applichiamo la regola odd-even per definire le regioni interne del poligono, possiamo individuare due span che stanno sulla linea di scansione e che sono interni al poligono. Una volta identificati gli span, possiamo colorare i pixel al loro interno usando il colore designato per il riempimento del poligono. E' dunque necessario determinare quali pixel sulla linea di scansione cadono all'interno del poligono, e quindi accenderli e colorarli in modo appropriato. Gli estremi degli span sono determinati dalle intersezioni del poligono con le linee di scansione, e possono essere calcolati per mezzo di un algoritmo incrementale che calcola l'intersezione tra una linea di scansione ed un lato a partire dall'intersezione con la linea di scansione considerata al passo precedente. Ripetendo questo processo per ogni linea di scansione che interseca il poligono, si ottiene la scan conversion dell'intero poligono.

Un metodo semplice per determinare gli estremi è quello di usare l'algoritmo di Bresenham per ottenere la scan conversion di ogni lato del poligono, e di mantenere una tabella con gli estremi degli span per ogni linea di scansione, aggiornandola ogni volta che un nuovo pixel viene prodotto. Si noti che questa strategia può produrre alcuni pixel che giacciono all'esterno del poligono, scelti dall'algoritmo di scan conversion poiché erano i più vicini ad un lato, indipendentemente dalla parte cui si trovavano (esterna o interna). L'algoritmo di scan conversion per i segmenti non ha infatti la nozione di regione interna e di regione esterna. Per i nostri scopi è tuttavia preferibile visualizzare solo i pixel che si trovano strettamente all'interno del poligono; pertanto è necessario modificare l'algoritmo di scan conversion dei segmenti in accordo a questo obiettivo.

Come nell'algoritmo di Bresenham originale, si utilizza un metodo incrementale per determinare gli estremi degli span su una linea di scansione, a partire da quelli calcolati al passo precedente, senza dovere calcolare le intersezioni tra linee di scansione e lati del poligono in modo analitico. Gli span sono riempiti con un processo che comprende tre fasi:

1. determinazione delle intersezioni della linea di scansione con tutti i lati del poligono;
2. ordinamento delle intersezioni secondo il valore crescente della coordinata x;
3. riempimento dei pixel tra le coppie delle intersezioni che giacciono all'interno del poligono, applicando il test odd-even per determinare quando un punto è interno.

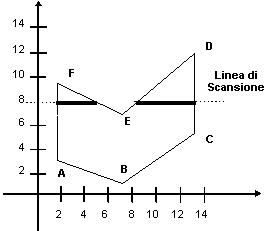Figura 4.11 Poligono con due gruppi di pixel sulla linea di scansione, interni al poligono.

Per prima cosa analizziamo la strategia di riempimento (fase 3). Poi considereremo le prime due fasi.

La fase di riempimento degli span richiede alcuni accorgimenti. Se un'intersezione avviene in corrispondenza di un valore di x frazionario, si deve stabilire quale pixel ai lati dell'intersezione sia interno e quale esterno; inoltre si devono considerare le possibili singolarità dovute alle intersezioni con coordinate intere, e cioè alla presenza di un lato o di un vertice esattamente sulla linea di scansione.

Il primo problema si risolve facendo in modo che quando ci si avvicina ad una intersezione frazionaria arrivando da sinistra e dall'interno del poligono, allora si arrotonda per difetto la coordinata x dell'intersezione in modo che sia individuato il pixel interno; se ci stiamo avvicinando dall'esterno dovremo invece arrotondare x per eccesso in modo da scegliere il pixel interno.

Anche nel caso di un lato che interseca la linea di scansione ad una coordinata intera, occorre stabilire se il pixel sia interno od esterno. Usando un criterio simile al precedente possiamo decidere che se il lato viene incontrato venendo da sinistra dall'esterno, il pixel è interno, se invece da sinistra e dall'interno il pixel è esterno.

Per quanto riguarda la questione delle singolarità sui vertici, osserviamo per prima cosa che ci sono tre casi da considerare, illustrati in figura 4.11.

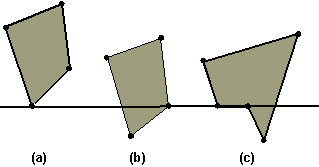Figura 4.12 Tre possibili singolarità.

Se stiamo utilizzando il test odd-even per il riempimento del poligono, i tre casi vanno trattati in modo differente. Nel primo caso non dobbiamo contare l'intersezione della linea di scansione con il vertice (oppure la possiamo contare due volte); nel secondo caso l'intersezione del vertice con la linea di scansione deve essere contata come se fosse l'attraversamento di un lato; nel terzo caso la linea di scansione ha numerose intersezioni con il lato orizzontale.

Una soluzione a questi casi è di non considerare il vertice più in alto di un lato. Nel caso (a) della figura, il vertice sulla linea viene considerato due volte; nel caso (b) il vertice sulla linea viene considerato una volta, in quanto viene scartato come vertice del lato che sta sotto la linea; nel caso (c) entrambi i vertici del lato orizzontale vengono scartati.

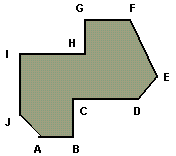Figura 4.13 Lati orizzontali di un poligono.

Un'altra tecnica è quella di considerare un frame buffer virtuale con una risoluzione doppia rispetto al frame buffer reale. Nel frame buffer virtuale i pixel sono posizionati solo nelle locazioni di ordinata y pari, mentre tutti i vertici sono posizionati in corrispondenza dei valori dispari di y.

Passiamo ora a considerare la prima fase del processo di scan conversion del poligono: la determinazione delle intersezioni. Un approccio un po' rudimentale sarebbe quello di testare ciascun lato del poligono per determinare le intersezioni con ogni linea di scansione. Tuttavia, solo pochi lati sono di interesse per una certa linea di scansione, inoltre molti dei lati intersecati dalla linea i sono intersecati anche dalla linea successiva, i + 1. Si parla a questo proposito di coerenza dei lati (edge coherence). La coerenza dei lati si verifica lungo un lato su tante linee di scansione quante quelle intersecate dal lato stesso. Muovendoci da una linea all'altra, possiamo calcolare le nuove intersezioni sulla base di quelle precedenti, applicando la stessa tecnica usata nell'algoritmo di Bresenham per calcolare il pixel successivo a partire da quello attuale.

Consideriamo le rette di pendenza maggiore di 1 che rappresentano lati di sinistra del poligono (i lati di destra e le altre pendenze sono trattate in modo analogo). Indichiamo con (x_min, y_min) e (x_max, y_max) gli estremi del lato. Nell'estremo inferiore (x_min, y_min) occorre accendere un pixel. Quando la coordinata y viene incrementata, la coordinata x del punto che giace sulla retta cui appartiene il lato, subisce un aumento pari a 1/m, dove m è la pendenza della retta:

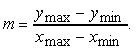
Questo incremento fa sì che x avrà una parte intera e una frazionaria, esprimibile da una frazione con al denominatore il fattore(y_max - y_min). Iterando il processo, la parte frazionaria crescerà fino a produrre un incremento per la parte intera. Quando la parte frazionaria di x è uguale a zero, possiamo accendere il pixel in posizione (x, y) che giace sulla retta; ma quando la parte frazionaria è diversa da zero dovremo arrotondarla in modo da disegnare il pixel che giace strettamente all'interno del poligono. Se la parte frazionaria eccede l'unità, incrementiamo x, sottraiamo 1 dalla parte frazionaria, e ci muoviamo di un pixel verso destra. Se incrementiamo x in modo da finire esattamente su un pixel, visualizziamo quel pixel, ma dobbiamo anche diminuire la frazione di un fattore pari a 1. Si osservi che possiamo evitare l'uso delle frazioni tenendo traccia solo del loro numeratore e osservando che la parte frazionaria è maggiore dell'unità quando il numeratore è maggiore di (y_max - y_min).

A questo punto siamo in grado di sviluppare l'algoritmo scan-line che sfrutta la coerenza dei lati, e che per ogni linea di scansione tiene traccia dell'insieme dei lati intersecati e dei punti di intersezione usando un'apposita struttura dati chiamata AET (dall'inglese active-edge table). I lati nella AET sono ordinati sulla base del valore x dell'intersezione, così che possiamo riempire gli span definiti dalle coppie dei valori di intersezione (opportunamente arrotondati), ossia dagli estremi degli span. Come ci muoviamo alla linea di scansione y a quella successiva, corrispondente a y + 1, la tabella AET viene aggiornata: i lati attualmente nella AET ma non intersecati dalla nuova linea di scansione (cioè i lati tali che y_max = y) vengono cancellati, e ogni nuovo lato intersecato (cioè tale che y_min = y + 1) viene aggiunto alla AET. Le nuove intersezioni sulle x vengono calcolate applicando la tecnica incrementale a tutti i lati che erano già nella AET, ma che non sono stati ancora completati.

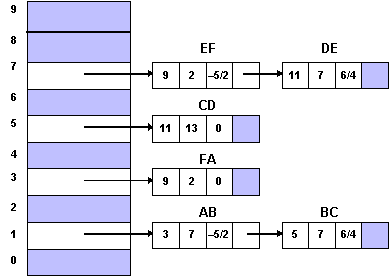Figura 4.14 Tabella ET.

Per rendere efficiente l'inserimento di nuovi lati nella AET, si crea inizialmente una tabella, detta ET (dall'inglese edge table) che contiene tutti i lati ordinati sulla base della loro coordinata y minore. La tabella ET è solitamente costruita usando un algoritmo di bucket sort, con tanti bucket quante le linee di scansione. Entro ogni bucket, i lati sono mantenuti in ordine crescente della coordinata x dell'estremo più basso. Ogni elemento nella ET contiene la coordinata y_max del lato, la coordinata x dell'estremo in basso (x_min), e l'incremento per le x usato nel passare da una linea di scansione alla successiva, .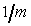

Una volta che la tabella ET è stata costruita, si completano i seguenti passi:

1. Si pone y pari al valore della coordinata y più piccola, che si trova nel primo bucket non vuoto.
2. Si inizializza la tabella AET.
3. Si ripete la seguente sequenza di operazioni fino a quando le tabelle AET e ET risultano vuote:
   1. Si rimuovono dal bucket y della ET i lati tali che y_max  = y, che vengono inseriti nella AET (lati entranti), e si ordina la AET rispetto a x (compito facilitato dal fatto che la ET è preordinata).
   2. Si riempiono i pixel negli span sulla linea di scansione y usando le coppie di coordinate x della AET.
   3. Si rimuovono dalla AET gli elementi tali che y = y_max (lati non coinvolti nella linea di scansione successiva).
   4. Si incrementa y di 1 per raggiungere la coordinata della linea di scansione successiva.
   5. Per ogni lato non verticale rimasto nella AET, si aggiorna la coordinata x in relazione al nuovo y.

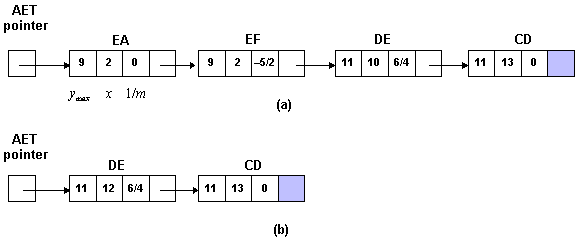Figura 4.15 AET per il poligono di figura 4.10, relativa alle linee di scansione 9 e 10.

Ai fini della scan conversion, i triangoli possono essere considerati casi speciali di poligoni, in cui ogni linea di scansione si interseca con due lati. Inoltre, dato che un poligono arbitrario può essere decomposto in un mesh di triangoli che condividono lati e vertici, possiamo effettuare la scan conversion dei poligoni decomponendoli prima in mesh di triangoli, e quindi effettuando la scan conversione delle componenti triangolari. La triangolazione è un problema classico della geometria computazionale, e si può fare efficientemente per i poligoni convessi, mentre il caso dei poligoni non convessi risulta più difficile da trattare.

1. Clipping dei segmenti lineari

Un altro compito fondamentale delle implementazioni è il clipping, ovvero il processo di determinare quali primitive, o parti di primitive, sono comprese nel volume di visualizzazione definito dal programma applicativo. Diremo che le primitive che cadono entro il volume di visualizzazione fissato sono accettate; mentre le primitive che non possono apparire sullo schermo sono eliminate, o rifiutate. Le primitive che cadono solo parzialmente entro il volume di visualizzazione devono essere tagliate in modo che tutte le parti che cadono al di fuori del volume siano rimosse.

Il clipping può essere eseguito analiticamente prima della scan conversion, oppure nel corso della stessa scan conversion. Per i pacchetti grafici che operano in aritmetica in virgola mobile, la soluzione migliore è quella di effettuare prima il clipping analitico nel sistema di coordinate in virgola mobile, e quindi la scan conversion delle primitive già ridotte. Per primitive più complesse di segmenti e poligoni, può comunque risultare conveniente effettuare il clipping nel corso della stessa scan conversion.

Nella libreria OpenGL si effettua il clipping delle primitive rispetto ad un volume tridimensionale prima di effettuare la scan conversion.

1. Algoritmo di Cohen-Sutherland

Il problema del clipping bidimensionale dei segmenti di linea è illustrato in figura 4.13.

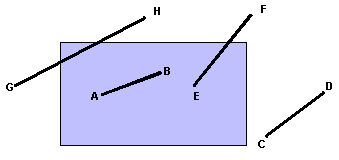Figura 4.16 Clipping bidimensionale dei segmenti.

Solo il segmento AB apparirà integralmente sullo schermo, mentre l'intero segmento CD sarà eliminato. I segmenti EF e GH dovranno invece essere accorciati prima di essere visualizzati.

Tutta l'informazione necessaria per il clipping può essere determinata calcolando le intersezioni tra le rette cui appartengono i segmenti e i bordi della finestra di clipping. Tuttavia, è preferibile evitare il calcolo delle intersezioni, se possibile, poiché ciascuna intersezione richiede una divisione in virgola mobile.

Nell'algoritmo di Cohen-Sutherland la maggior parte di moltiplicazioni e divisioni in virgola mobile è sostituita da una combinazione di sottrazioni in virgola mobile e operazioni su bit.

I lati della finestra di clipping vengono estesi idealmente all'infinito, dividendo il piano in nove regioni. Ad ogni regione si assegna un codice binario b₀b₁b₂b₃ composto di quattro bit e chiamato outcode. Dato un punto (x, y), l'outcode si definisce nel modo seguente. Si pone

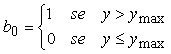
e analogamente si pone b₁ uguale a 1 se y  < y_max; b₂ e b₃ sono invece determinati dalle relazioni tra x e i bordi sinistro e destro della finestra di visualizzazione. Si osservi che la regione che corrisponde alla finestra di visualizzazione è caratterizzata dall'outcode 0000.

Il primo passo dell'algoritmo consiste nel calcolare gli outcode degli estremi del segmento, passo che può richiedere otto sottrazioni in virgola mobile per ciascun segmento. Consideriamo ora un segmento i cui outcode siano dati da o₁ = outcode(x₁, y₁) e o₂ = outcode(x₂, y₂). Ci sono quattro casi da considerare (figura 4.15).

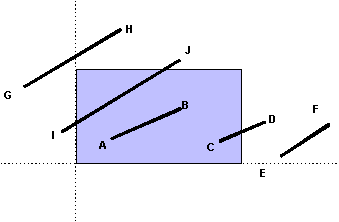Figura 4.18 Casi per gli outcode nell'algoritmo di Cohen-Sutherland.

o₁ = o₂ = 0000
Entrambi gli estremi giacciono all'interno della finestra di clipping (segmento AB). Dunque l'intero segmento cade all'interno della finestra, e può essere inviato alla fase di scan conversion.

o₁  0000, o₂ = 0000 (o viceversa)
Un estremo cade all'interno della finestra di visualizzazione, mentre l'altro cade all'esterno (segmento CD): il segmento deve essere accorciato. L'outcode diverso da zero indica quale lato, o quali lati, della finestra sono intersecati dal segmento. È necessario calcolare una o due intersezioni. Si osservi che, dopo che una intersezione è stata calcolata, possiamo calcolare l'outcode del punto di intersezione per determinare se è necessario calcolare un'altra intersezione.

o₁  o₂  0000
Calcolando l'AND logico degli outcode possiamo determinare se i due estremi giacciono o meno nella stessa regione al di fuori della finestra. In questo caso l'intero segmento deve essere rifiutato (segmento EF).

o₁  o₂ = 0000
Entrambi gli estremi sono all'esterno della finestra di clipping, ma cadono all'esterno di bordi differenti. Come risulta evidente esaminando i casi dei segmenti GH e IJ nella figura 4.15, non è possibile determinare esclusivamente sulla base degli outcode se il segmento può essere eliminato o deve essere solo accorciato. La cosa migliore da fare in questo caso è calcolare l'intersezione con uno dei lati della finestra e controllare l'outcode del punto risultante.

I controlli effettuati sugli outcode richiedono solo operazioni Booleane, e le intersezioni vengono calcolate solo quando necessario, cioè quando gli outcode non contengono un'informazione sufficiente.

Il calcolo delle intersezioni dipende da come scegliamo di rappresentare il segmento di linea. Se utilizziamo la forma esplicita di una retta, y = mx + h, possiamo calcolare la pendenza m e l'ordinata h del punto di intersezione con l'asse y direttamente dagli estremi. Tuttavia, le rette verticali non possono essere rappresentate con questa forma, e in questo caso può essere conveniente applicare algoritmi differenti per il clipping, basati sulla rappresentazione parametrica delle rette.

L'algoritmo di Cohen-Sutherland è quindi il seguente:
typedef struct {unsigned all;unsigned left:1;unsigned right:1;unsigned bottom:1;unsigned top:1;} outcode;
void clipAndDraw(float x0, float y0, float x1, float y1, float xmin, float xmax, float ymin, float ymax, int color){ boolean accept, done; outcode outcode0, outcode1, outcodeOut, compOutCode(); float x, y; accept = false; done = true; outcode0 = compOutCode(x0, y0, xmin, xmax, ymin, ymax); outcode1 = compOutCode(x1, y1, xmin, xmax, ymin, ymax); do { if (outcode0.all == 0 && outcode1.all == 0) { accept = true; done = true; } else if (outcode0.all & outcode1.all != 0) done = true; else { if (outcode0.all != 0) outcodeOut = outcode0; else outcodeOut = outcode1; if (outcodeOut.top) { /* dividi la linea sul bordo superiore del rettangolo */ x = x0 + (x1 - x0) * (ymax - y0) / (y1 - y0); y = ymax; } else if (outcodeOut.bottom) { /* dividi la linea sul bordo inferiore del rettangolo */ x = x0 + (x1 - x0) * (ymin - y0) / (y1 - y0); y = ymin; } else if (outcodeOut.right) { /* dividi la linea sul bordo destro del rettangolo */ y = y0 + (y1 - y0) * (xmax - x0) / (x1 - x0); x = xmax; } else if (outcodeOut.left) { /* dividi la linea sul bordo sinistro del rettangolo */ y = y0 + (y1 - y0) * (xmin - x0) / (x1 - x0); x = xmin; } if (outcodeOut.all == outCode0.all) { x0 = x; y0 = y; outcode0 = compOutCode(x0, y0, xmin, xmax, ymin, ymax); } else { x1 = x; y1 = y; outcode1 = compOutCode(x1, y1, xmin, xmax, ymin, ymax); } } /* Suddividi */ } while (!done); if (accept) drawLine(x0, y0, x1, y1, color);} outcode compOutcode(float x, float y, float xmin, float ymin, float ymax){outcode code;code.all = 0;if (y > ymax) {code.top = 1;cpde.all += code.top;} else if (y < ymin) {code.bottom = 1;code.all += code.bottom;}if (x > xmax) {code.right = 1;code.all += code.right;} else if (x < xmin) {code.left = 1;code.all += code.left;}return code;}

Possiamo esaminare come si comporta l'algoritmo nel caso illustrato nella figura 4.16. La linea AE richiede diverse iterazioni. Il primo punto, A, ha outcode 0100, perciò l'algoritmo lo sceglie come punto esterno ed esamina l'outcode per scoprire che il bordo che tagli a la linea è quello inferiore, per cui AE viene ridotto a BE. Nella seconda iterazione, BE non può essere direttamente accettato o rifiutato. L'outcode del primo punto, B, è 0000, perciò l'algoritmo sceglie il punto esterno E, che ha codice 1010. Perciò il taglio avviene rispetto al bordo superiore, producendo BD. Il codice di H risulta essere 0010, perciò la terza iterazione produce un taglio rispetto al bordo destro, ottenendo BC. Questa linea viene accettata nella quarta iterazione e disegnata.

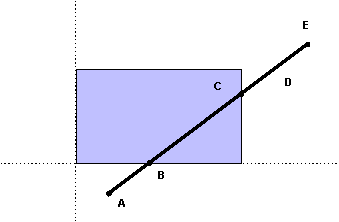Figura 4.19 Clipping con algoritmo Cohen-Sutherland

1. Algoritmo di Liang-Barsky

Se utilizziamo la rappresentazione parametrica, possiamo affrontare il problema del clipping dei segmenti lineari in un modo diverso e, in ultima analisi, più efficiente.

Supponiamo di avere un segmento lineare definito da due estremi, che rappresentiamo in forma vettoriale

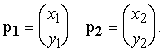
Possiamo usare questi estremi per definire l'unica retta su cui giace il segmento in modo parametrico, attraverso la seguente forma vettoriale

p(a) = (1 - a)p₁ + a p₂

o sotto forma di due equazioni scalari

x(a) = (1 - a)x₁ + a x₂

y(a) = (1 - a)y₁ + a y₂

Al variare del parametro tra 0 e 1, ci si muove lungo il segmento, da p₁ a p₂. I valori negativi di forniscono i punti sulla retta che precedono p₁, mentre i valori maggiori di 1 corrispondono ai punti sulla retta compresi tra p₂ e l'infinito.

Consideriamo un segmento e la retta cui appartiene (figura 4.17). Se la retta non è parallela ad uno dei lati della finestra di clipping (se ciò si verifica, la situazione risulta comunque molto semplice da trattare), ci sono quattro punti di intersezione tra la retta e le estensioni dei lati della finestra.

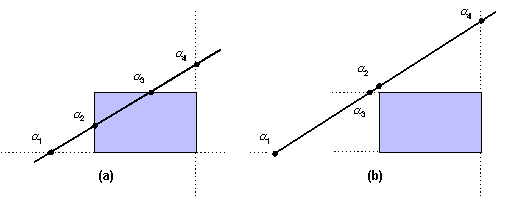Figura 4.20 Due casi di retta parametrica e finestra di clipping.

Questi punti corrispondono ai quattro valori del parametro : ₁, ₂, ₃ e ₄. Nell'esempio che stiamo esaminando (figura 4.17 (a)), risulta 1 > ₄ > ₃ > ₂ > ₁> 0. Quindi, le quattro intersezioni cadono tutte entro il segmento originale, e le due più interne (₂  e ₃) determinano il segmento accorciato che verrà visualizzato. Questo caso si differenzia da quello illustrato in figura 4.17 (b), in cui le quattro intersezioni sono ancora all'interno del segmento, ma in cui l'ordine è diventato 1 > ₄ > ₃ > ₂ > ₁> 0. In questo caso, la linea interseca le estensioni dei lati superiore e inferiore della finestra prima di intersecare quelle dei lati destro e sinistro; questo significa che l'intero segmento deve essere rifiutato. I casi corrispondenti ad altri ordinamenti dei punti di intersezione possono essere argomentati in modo analogo.

Per implementare in modo efficiente di questa strategia occorre evitare di calcolare le intersezioni, fino a quando esse non risultano necessarie. Molti segmenti possono infatti essere rifiutati prima di conoscere le coordinate dei quattro punti di intersezione. L'intersezione con il lato superiore della finestra, si trova in corrispondenza del valore

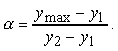
Equazioni analoghe valgono per gli altri tre lati della finestra di visualizzazione. Per evitare le divisioni, possiamo scrivere l'equazione nella forma a(y₂ - y₁) = aDy = y_max - y₁ = Dy_max

Tutti i test richiesti dall'algoritmo possono essere riformulati in termini di Dy_max e di Dy, e termini simili possono essere calcolati per gli altri lati della finestra. Quindi, tutte le decisioni relative al clipping possono essere prese senza alcuna divisione in virgola mobile. La divisione verrà effettuata solo quando l'intersezione va calcolata per accorciare un segmento.

1. Clipping dei poligoni

Un algoritmo che effettua il clipping dei poligoni deve prendere in considerazione diversi casi, come si può facilmente comprendere osservando la figura 4.18.

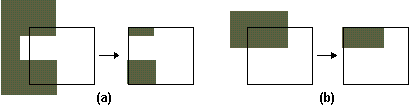Figura 4.21 Esempi di clipping di poligoni: (a) componenti multiple; (b) poligono convesso semplice.

L'esempio in figura 4.18 (a) è particolarmente interessante, in quanto il risultato del clipping del poligono concavo è dato da due poligoni separati.

Il compito del clipping dei poligoni appare dunque piuttosto complesso. Ogni lato del poligono deve essere confrontato con ogni lato del rettangolo di clipping; devono essere aggiunti nuovi lati, e alcuni lati esistenti devono invece essere eliminati, accorciati, oppure divisi.

Possiamo generare gli algoritmi di clipping per i poligoni direttamente da quelli per i segmenti, effettuando il clipping di ciascun lato del poligono individualmente. Ad esempio, per il clipping rispetto ad aree rettangolari, si possono applicare sia l'algoritmo di CohenñSutherland che quello di LiangñBarsky. Esiste tuttavia un altro approccio, che ora analizzeremo.

1. Algoritmo di Sutherland-Hodgman

L'algoritmo di clipping dei poligoni di Sutherland-Hodgman utilizza una strategia divide et conquer: risolve una serie di problemi semplici e identici che, una volta combinati, forniscono la soluzione del problema globale di partenza. Il problema di base è quello del clipping del poligono rispetto ad un solo lato, di lunghezza infinita. Il clipping complessivo del poligono si ottiene ripetendo questa operazione di base rispetto a ciascuno dei quattro lati della finestra di visualizzazione.

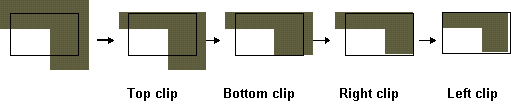Figura 4.22 Clipping di un poligono lato per lato.

L'algoritmo di Sutherland-Hodgman è molto generale e consente di effettuare il clipping di qualsiasi poligono (concavo o convesso) rispetto ad un qualsiasi altro poligono convesso di clipping; inoltre, esso può essere esteso al caso tridimensionale.

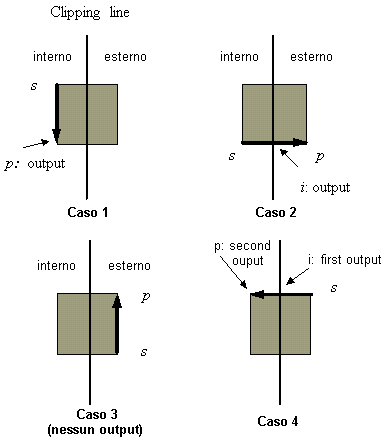Figura 4.23 Quattro casi di clipping di poligoni.

L'algoritmo riceve in input i vertici del poligono, ed esamina ad ogni passo le relazioni tra i vertici e il lato di clipping considerato. Ad ogni passo, viene così determinata una coppia di vertici, che corrisponde al lato del poligono una volta effettuato il clipping, oppure viene determinato un solo vertice, o nessun vertice, se il lato giace al di fuori del bordo di clipping. Ci sono quattro casi da analizzare (si veda la figura 4.20). Consideriamo il lato del poligono dal vertice s al vertice p nella figura 4.20. Supponiamo che il punto di partenza s sia già stato trattato nell'iterazione precedente. Nel caso 1, quando il lato del poligono è completamente all'interno del bordo di clipping, il vertice p viene aggiunto alla lista di output. Nel caso 2, il punto i di intersezione viene restituito in output come vertice poiché il lato interseca il lato di clipping. Nel caso 3, entrambi i vertici sono all'esterno del bordo e non ci sarà alcun output. Infine, nel caso 4, il punto i di intersezione e il vertice p sono aggiunti alla lista di output.

Supponiamo ora di considerare il clipping rispetto al lato superiore della finestra di visualizzazione. Possiamo vedere questa operazione come una sorta di scatola nera, i cui input e output sono coppie di vertici, e dove il valore y_max è un parametro noto (figura 4.21). Sfruttando i triangoli simili (figura 4.22), se c'è una intersezione, questa giace nel punto di coordinate

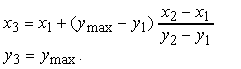
L'operazione di clipping restituisce dunque una delle tre coppie {(x₁, y₁), (x₂, y₂)}, {(x₁, y₁), (x_i, y_max)} oppure {(x_i, y_max), (x₂, y₂)}.

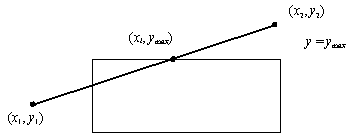Figura 4.21 Clipping rispetto al lato superiore.

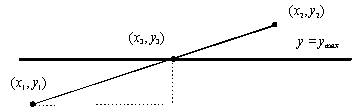Figura 4.24 Intersezione col lato superiore della finestra di clipping.

Possiamo quindi effettuare il clipping rispetto agli altri tre lati, indipendentemente, usando le stesse equazioni e scambiando il ruolo delle x e delle y in modo opportuno, così come i valori dei lati della finestra di clipping (figura 4.22).

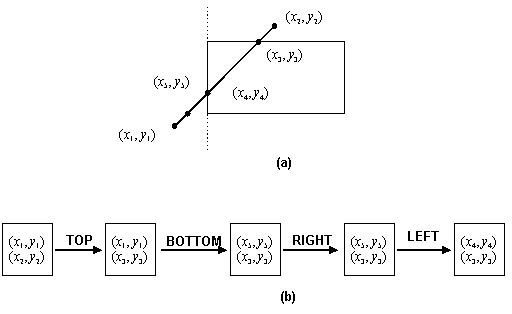Figura 4.25 (a) Problema di clipping; (b) Pipeline di clipping.

L'algoritmo di Sutherland-Hodgman è il seguente:
typedef vertex { float x, y;}
typedef vertex edge[2];typdef vertex polygon[MAX];
void intersect(vertex first, vertex second, edge clipBoundary, vertex *intersect){ if (clipBoundary[0].y == clipBoundary[1].y; { /* orizzontale */ intersect->y = clipBoundary[0].y; intersect->x = first.x + (clipboundary[0].y - first.y) * (second.x -firrst.x) / (second.y -first.y); } else { /* verticale */ if (clipBoundary[0].x == clipBoundary[1].x; { intersect->x = clipBoundary[0].x; intersect->y = first.y + (clipboundary[0].x - first.x) * (second.y -firrst.y) / (second.x -first.x); }}
boolean inside(vertex v, edge clip){if (clip[1].x > clip[0].x) /* basso */ return (v.y >= clip[0].y);if (clip[1].x < clip[0].x) /* alto */ return (v.y <= clip[0].y);if (clip[1].y > clip[0].y) /* destra */ return (v.x >= clip[1].x);if (clip[1].y < clip[0].y) /* sinistra */ return (v.x >= clip[0].x); return false;}
void output(vertex new, int* count, polygon poly){poly[*count].x = new.x;poly[*count].y = new.y; (*count)++;}
void polygonClip(polygon poly, polygon clipped, int inCount, int *outCount, polygon clip){ vertex s, p, i; int j;
*outCount = 0; s = poly[inCount - 1]; /* comincia dall'ultimo vertice */ for (j = 0; j < inCount; j++) { p = poly[j]; if (inside(p, clip)) { /* casi 1 e 4 */ if (inside(s, clip)) /* caso 1 */ output(p, outCount, clipped); else { /* caso 4 */ intersects(s, p, clip, &I); output(i, outCount, clipped); output(p, outCount, clipped); } else if (inside(s, clip)) { /* caso 2 */ intersects(s, p, clip, &I); output(i, outCount, clipped); } /* caso 3: vuoto */ s = p; /* passa alla prossima coppia di vertici */ }}

1. Antialiasing

La scan conversion dei segmenti e dei poligoni può apparire disturbata da alcuni difetti di visualizzazione, anche quando si utilizzano schermi con una risoluzione dell'ordine di 1024  1280. Questo difetti si verificano tutte le volte che cerchiamo di passare dalla rappresentazione continua di un oggetto, che ha una risoluzione infinita, alla sua approssimazione discreta, che ha invece una risoluzione limitata. A questo fenomeno si dà il nome di aliasing, e l'applicazione di tecniche che riducono e eliminano l'aliasing, è detta antialiasing.

Gli errori sono causati da tre problemi collegati alla natura discreta del frame buffer. Per prima cosa, se abbiamo un frame buffer n  m, il numero di pixel è fissato, e possiamo generare solo certi pattern per approssimare i segmenti. Molti segmenti tra loro diversi potrebbero così essere approssimati dallo stesso pattern di pixel. In secondo luogo, le locazioni dei pixel sono fissate su una griglia uniforme; ed infine, i pixel hanno una dimensione e una forma fissate.

Nonostante le rette siano entità monodimensionali che hanno una lunghezza ma non una ampiezza, le rette ottenute con la scan conversion devono avere un'ampiezza per poter essere visibili. Una primitiva, una volta rasterizzata, occupa un'area finita dello schermo. Quindi possiamo pensare al nostro segmento come ad un rettangolo con un certo spessore, che copre una parte della griglia di pixel. Possiamo allora osservare che un segmento non dovrebbe accendere un solo pixel di una colonna usando il colore nero, ma piuttosto dovrebbe visualizzare più di un pixel per riga o colonna, con una intensità opportuna. Allora, per le linee di ampiezza pari ad un pixel, solo quelle verticali e orizzontali dovrebbero influenzare esattamente un pixel per colonna e riga, rispettivamente; mentre per le linee di pendenza diversa, più di un pixel deve essere visualizzato in una riga o una colonna.

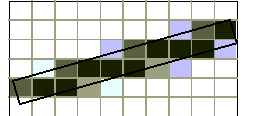Figura 4.26 Antialiasing

Supponiamo che ciascun pixel sia un quadrato di lato unitario, centrato su un punto della griglia, e che possa occupare un box di altezza e ampiezza unitarie sullo schermo. Supponiamo inoltre che una linea contribuisca all'intensità dei pixel per un ammontare proporzionale alla percentuale del pixel che essa copre. Un pixel pienamente coperto su un display in bianco e nero, sarà colorato in nero, mentre un pixel parzialmente ricoperto sarà colorato con un'opportuna sfumatura di grigio, di intensità proporzionale alla copertura del pixel da parte della linea. I pixel che non sono intersecati dalla linea restano bianchi. In questo modo, la linea appare più liscia e continua.

Questa tecnica è chiamata unweighted area sampling. Vi è una strategia ancora più efficace, che è invece chiamata weighted area sampling. Per vedere le differenze tra le due tecniche è opportuno prima analizzare alcune proprietà della tecnica unweighted. Per prima cosa, l'intensità dei pixel intersecati dalla linea decresce all'aumentare della distanza tra il centro del pixel e la linea stessa: più la primitiva è lontana, minore è la sua influenza sull'intensità del pixel. Questa relazione è ovviamente vera poiché l'intensità diminuisce al diminuire dell'area di sovrapposizione, e tale area diminuisce quando la linea si allontana dal centro del pixel, e si avvicina ai bordi. Quando la linea ricopre completamente il pixel, l'area di intersezione, e quindi l'intensità sono massime. Se la primitiva è solo tangente al contorno del pixel, l'area di sovrapposizione, e quindi la sua intensità sono nulle.

Una seconda proprietà dell'unweighted area sampling è che una primitiva non può influenzare l'intensità di un pixel, se non lo interseca. Infine, una terza proprietà di questa tecnica è che aree uguali contribuiscono nello stesso modo all'intensità, indipendentemente dalla distanza tra il centro del pixel e l'area. Ciò che importa è solo l'ampiezza dell'area di sovrapposizione. Così una piccola area nell'angolo del pixel contribuisce esattamente come un'area della stessa ampiezza, ma posta in prossimità del centro del pixel.

Nella tecnica weighted, si mantengono le prime due proprietà della tecnica precedente, mentre si interviene sulla terza, facendo in modo che aree di uguale ampiezza possano contribuire diversamente: un'area più vicina al centro del pixel avrà un'influenza maggiore sulla sua intensità rispetto ad una a distanza maggiore.

Per mantenere la seconda proprietà (le primitive contribuiscono solo all'intensità dei pixel che intersecano) dobbiamo operare una variazione sulla geometria dei pixel. Nella tecnica unweighted, se il bordo della primitiva è prossimo al contorno del quadrato che rappresenta il pixel, ma non lo interseca, non contribuisce all'intensità. In questo nuovo approccio, ogni pixel è rappresentato da un'area circolare più larga del quadrato. La primitiva interseca così un'area più ampia, e quindi contribuisce all'intensità del pixel. Si osservi che questo significa che le aree associate a pixel adiacenti si sovrappongono parzialmente. Si definisce inoltre una funzione filtro che determina quanto un'area dA della primitiva influenza l'intensità di un pixel, in funzione della distanza di quest'area dal centro del pixel. Possiamo pensare alla funzione filtro come ad una funzione W(x, y) sul piano, la cui altezza fornisce il peso dell'area nel punto (x, y). Il contributo all'intensità di un pixel si determina calcolando l'integrale della funzione sull'area di sovrapposizione tra il pixel e la primitiva. Se indichiamo con W_S il valore dell'integrale (compreso tra 0 e 1), e con I_max il valore massimo dell'intensità, l'intensità I attribuita al pixel risulta uguale a I_max  W_S.

Nella scelta della funzione filtro si deve fare in modo che questa dia un peso minore alle aree più lontane al centro del pixel, e un peso maggiore a quelle più vicine. Ad esempio, una funzione che assume valore massimo nel centro del pixel, e valori decrescenti linearmente all'aumentare della distanza dal centro rappresenta una buona scelta. A causa della simmetria rotazionale, il grafico di questa funzione forma un cono circolare, la cui base, chiamata supporto del filtro, dovrebbe avere un raggio pari alla distanza unitaria sulla griglia, per fare in modo che un primitiva piuttosto lontana dal centro possa comunque contribuire, anche se di poco, all'intensità del pixel.

Il filtro di forma conica presenta due proprietà molto utili: simmetria rotazionale e diminuzione lineare della funzione con la distanza radiale. Scelte più ottimali, possono risultare computazionalmente più costose. I filtri conici rappresentano dunque un buon compromesso tra costo e qualità dell'immagine ottenibile.

Un'altra tecnica per ottenere l'antialiasing consiste nell'utilizzare il canale a del colore.