 Figura 3.1 Libreria
grafica
Figura 3.1 Libreria
graficaIl progresso dei dispositivi hardware di output grafico ha determinato, in modo del tutto naturale, uníevoluzione delle applicazioni software e ha portato alla realizzazione di librerie grafiche di alto livello, indipendenti da qualsiasi periferica grafica di input e output e con una portabilità simile a quella dei linguaggi di programmazione di alto livello (quali FORTRAN, Pascal, o C).
Il modello concettuale alla base delle prime librerie grafiche (bidimensionali) realizzate è quello ora definito modello pen plotter, con chiaro riferimento al dispositivo output allora disponibile. Un pen plotter produce immagini muovendo una penna lungo due direzioni sulla carta; la penna può essere alzata e abbassata come richiesto per creare líimmagine desiderata. Diverse librerie grafiche ñ come LOGO, GKS, e PostScript ñ sebbene diverse líuna dallíaltra, hanno in comune proprio il fatto di considerare il processo di creazione delle immagini simile al processo di disegnare una figura su un pezzo di carta: líutente ha a disposizione una superficie bidimensionale, e vi muove sopra una penna lasciando uníimmagine.
Questi sistemi grafici possono essere descritti con
due funzioni di drawing:
moveto(x, y);lineto(x, y);
Líesecuzione della funzione moveto muove la penna alla locazione (x, y) sul foglio, senza lasciare segni. La funzione lineto muove la penna fino alla posizione (x, y) e disegna una linea dalla vecchia alla nuova locazione della penna. Aggiungendo qualche procedura di inizializzazione e terminazione, la possibilità di cambiare penna per variare il colore e lo spessore delle linee, abbiamo dunque un sistema grafico, semplice ma completo.
Per alcune applicazioni, quali il layout di pagina, i sistemi costruiti su questo modello sono sufficienti. Questo è il caso, ad esempio, del linguaggio PostScript, uníestensione sofisticata di queste idee di base oggi ampiamente utilizzato per la descrizione di pagine, in quanto rende relativamente facili gli scambi elettronici di documenti contenenti sia testo che immagini grafiche in due dimensioni.
Il sistema X window, ormai uno standard per le workstation UNIX, è usato sia per ottenere una finestra su un display grafico, in cui possono essere visualizzati sia testi che grafica 2D; che come mezzo standard per ottenere input da dispositivi quali tastiera e mouse. Líadozione di X dalla maggior parte di compagnie che realizzano workstation, ha avuto il seguente effetto: un singolo programma può produrre grafica 2D su uníampia varietà di workstation, semplicemente ricompilando il programma. Questa integrazione funziona anche sulle reti: il programma può essere eseguito su una workstation, ma visualizzare líoutput o ricevere líinput da uníaltra, anche se le workstation in rete sono state costruite da compagnie diverse.
Il modello pen plotter non si estende bene ai sistemi grafici 3D. Ad esempio, se vogliamo usare un modello pen plotter per produrre uníimmagine di un oggetto tridimensionale su una superficie bidimensionale, è necessario proiettare sulla nostra superficie punti nello spazio tridimensionale. Tuttavia, è preferibile utilizzare uníinterfaccia grafica che consenta allíutente di lavorare direttamente nel dominio del problema, e di utilizzare il computer per eseguire i dettagli del processo di proiezione in modo automatico, senza che líutente debba eseguire calcoli trigonometrici.
Per la grafica tridimensionale sono stati proposti diversi standard, ma ancora nessuno ha ottenuto uníampia accettazione. Una libreria relativamente ben nota è il pacchetto PHIGS (dallíinglese Programmerís Hierarchical Interactive Graphics System), così come il suo discendente PHIGS+. Basata su GKS (Graphics Kernel System), PHIGS è uno standard ANSI (American National Standard Institute) che consente di manipolare e realizzare immagini di oggetti in tre dimensioni, incapsulando la descrizione degli oggetti e dei loro attributi in una display list cui si fa riferimento ogni volta che si visualizza o si deve manipolare líoggetto. Il vantaggio delle display list è che è sufficiente una sola descrizione degli oggetti, anche se questi vengono poi visualizzati diverse volte, mentre un possibile svantaggio è dovuto allo sforzo considerevole che le display list richiedono per specificare nuovamente un oggetto quando esso viene modificato in seguito alle interazioni con líutente.
La libreria PEX (acronimo per PHIGS Extension to X) è uníestensione di X che consente di manipolare e realizzare oggetti 3D, e di ottenere un rendering in modo immediato, ossia di visualizzare gli oggetti così come sono descritti senza dover prima compilare una display list. Una difficoltà legata allíuso della libreria PEX è dovuta al fatto che i fornitori di interfacce PEX hanno scelto di consentire caratteristiche diverse, rendendo la portabilità dei programmi problematica. Inoltre, la libreria PEX è priva di caratteristiche di rendering avanzate, ed è disponibile solo agli utenti X.
OpenGL è una libreria grafica piuttosto recente, che consente di realizzare e manipolare immagini in due e tre dimensioni, e utilizza inoltre le tecniche più avanzate di rendering, sia in modo immediato, che attraverso display list. » molto simile, sia nella sua funzionalità che interfaccia, a IRIS GL della Silicon Graphics.
Come le librerie menzionate, OpenGL è uníinterfaccia software per hardware grafico. Líinterfaccia consiste di un insieme di diverse centinaia di funzioni e procedure che consentono al programmatore di specificare gli oggetti e le operazioni coinvolte nella produzione di immagine grafiche di alta qualità, quali immagini a colori di oggetti tridimensionali. Come il pacchetto PEX, OpenGL integra la grafica 3D nel sistema X, ma può essere integrato in altri sistemi window, o utilizzato senza alcun sistema window. Rispetto ad altre librerie, OpenGL è facile da imparare ed è anche piuttosto potente.
OpenGL è stata derivata dallíinterfaccia GL, sviluppata per le workstation Silicon Graphics, e progettata per il rendering in tempo reale, ad alta velocità. OpenGL è il risultato dei tentativi di trasferire i vantaggi di GL ad altre piattaforme hardware: sono state rimosse funzioni input e windowing e ci si è concentrati sugli aspetti di rendering dellíinterfaccia, realizzando così una libreria estremamente portabile, e conservando allo stesso tempo le caratteristiche che hanno fatto di GL uníinterfaccia molto potente per i programmi di applicazione.
OpenGL fornisce un controllo diretto sulle operazioni fondamentali di grafica in due e tre dimensioni. Ciò include la specificazione di parametri quali matrici di trasformazione, o operazioni di aggiornamento dei pixel. Inoltre, OpenGL non impone un particolare metodo per la descrizione degli oggetti geometrici complessi, ma fornisce piuttosto i mezzi di base per mezzo dei quali gli oggetti, indipendentemente da come siano stati descritti, possono essere ottenuti.
Analizziamo ora, in modo schematico, il funzionamento di OpenGL. Per prima cosa, possiamo pensare al nostro pacchetto grafico come ad una scatola nera, ossia un sistema le cui proprietà sono descritte solo per mezzo di input e output; senza che nulla sia noto sul suo funzionamento interno. In particolare, gli input sono costituiti dalle funzioni chiamate dal programma applicativo, dagli input provenienti da altri dispositivi quali mouse e tastiera, ed infine dai messaggi del sistema operativo. Gli output sono per la maggior parte di tipo grafico, sono infatti prevalentemente costituiti da primitive geometriche da visualizzare sullo schermo del CRT. Questo stesso schema caratterizza anche molte altre librerie grafiche.
 Figura 3.1 Libreria
grafica
Figura 3.1 Libreria
graficaLe primitive geometriche sono disegnate in un frame buffer sulla base di alcuni attributi. Ogni primitiva geometrica, che può essere un punto, un segmento, un poligono, un pixel o una bitmap, è definita da gruppi di uno o più vertici. Un vertice definisce un punto, líestremo di un lato, il vertice di un poligono dove due lati si incontrano. Gli attributi possono essere cambiati indipendentemente, e il setting degli attributi relativi ad una primitiva non influenza il setting degli attributi di altre. I dati (coordinate e attributi) sono associati ai vertici, ed ogni vertice è processato indipendentemente.
La specificazione di attributi e primitive e la descrizione delle altre operazioni avviene inviando comandi sotto forma di chiamate di funzioni o procedure. Le funzioni contenute in una libreria grafica possono essere classificate a seconda della loro funzionalità:
I nomi delle funzioni di OpenGL iniziano con le lettere gl e sono memorizzate in una libreria, usualmente detta GL. Líutente può inoltre avvalersi di altre librerie collegate. Una è la libreria GLU (dallíinglese graphics utility library), che usa solo funzioni GL, e contiene il codice per oggetti comuni, quali ad esempio sfere, che líutente preferisce non dover descrivere ripetutamente. Questa libreria è disponibile in tutte le implementazioni OpenGL. Una seconda libreria, GLUT (dallíinglese GL utility toolkit) si occupa della gestione delle interfacce con il sistema window. Fornisce la funzionalità minima aspettata da qualsiasi sistema moderno di windowing.
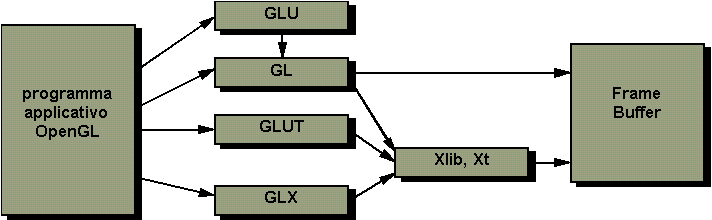 Figura 3.2 Organizzazione
delle librerie.
Figura 3.2 Organizzazione
delle librerie.Nella Figura 3.3 è illustrato un diagramma schematico del funzionamento di OpenGL. La maggior parte dei comandi inviati a OpenGL può venire accumulata in una display list, che viene processata successivamente. Altrimenti i comandi sono inviati attraverso un processing pipeline. Durante il primo stadio vengono approssimate curve e superfici geometriche valutando funzioni polinomiali sui valori di input. Nel secondo stadio si opera sulle primitive geometriche descritte dai vertici: i vertici sono trasformati e illuminati, e le primitive sono tagliate al volume di osservazione, per essere inviate allo stadio successivo, la rasterizzazione. La rasterizzazione produce una serie di indirizzi e valori per il frame buffer, utilizzando una descrizione bidimensionale di punti, segmenti e poligoni. Ogni frammento così prodotto viene quindi inviato allo stadio successivo in cui si eseguono delle operazioni sui frammenti individuali, prima che essi finalmente modifichino il frame buffer. Queste operazioni includono, oltre alle operazioni logiche sui valori dei frammenti, líaggiornamento del frame buffer in base ai dati in entrata memorizzati precedentemente, e la colorazione dei frammenti entranti con i colori memorizzati. Infine, i rettangoli di pixel e le bitmap possono bypassare lo stadio relativo allíelaborazione dei vertici, ed inviare, attraverso la rasterizzazione, blocchi di frammenti alle operazioni sui frammenti individuali.
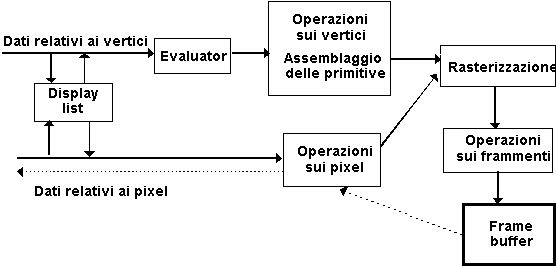 Figura 3.3 Diagramma
a blocchi di OpenGL
Figura 3.3 Diagramma
a blocchi di OpenGLAllíinterno della comunità grafica cíè stato un ampio dibattito riguardante quali e quante primitive dovrebbero essere mantenute in una libreria grafica, dibattito non ancora del tutto risolto. Da un lato cíè chi sostiene che le librerie dovrebbero contenere un insieme ristretto di primitive, quelle che tutti i sistemi hardware sono in grado di gestire. Inoltre queste primitive dovrebbero essere ortogonali, nel senso che ciascuna dovrebbe garantire allíutente delle possibilità non ottenibili dalle altre. Questi sistemi minimali di solito mantengono primitive quali linee, poligoni e qualche forma di testo (stringhe di caratteri), tutte generabili dallíhardware in modo efficiente. Dallíaltro lato ci sono le librerie che possono mantenere una grossa varietà di primitive, tra cui anche cerchi, curve, superfici e solidi. Líidea è quella di rendere disponibili primitive più complesse, al fine di rendere líutente in grado di realizzare applicazioni più sofisticate. Tuttavia, poiché pochi sistemi hardware sono in grado di sostenere questa varietà di primitive, i programmi basati su questi pacchetti grafici risultano poco portabili.
OpenGL sta in una posizione intermedia tra le due tendenze. La libreria di base contiene un insieme limitato di primitive, mentre la libreria GLU contiene un insieme molto ricco di oggetti derivati dalle primitive di base.
Le primitive di base di OpenGL sono specificate attraverso
una serie di vertici. Il programmatore definisce quindi un oggetto
attraverso una sequenza di comandi della forma
glBegin(type);glVertex*(
. . . );..glVertex*( . . . );glEnd();
Il comando glVertex*();
si usa per specificare un singolo vertice.
OpenGL mette a disposizione dellíutente diverse forme per
descrivere un vertice, in modo che líutente possa selezionare
quella più adatta al problema. Il carattere * può
essere interpretato come due o tre caratteri della forma nt
o ntv, dove
n indica
il numero di dimensioni (2, 3, o 4); t denota il tipo di dati
(interi (i),
virgola mobile (f),
doppia precisione (d));
infine la presenza del carattere v
indica che le variabili sono specificate per mezzo di un puntatore
ad un vettore o ad una lista. Ad esempio, se si vuole lavorare
in due dimensioni, usando gli interi, allora il comando più
appropriata è
glVertex2i(GLint x, GLint y);
mentre il comando
glVertex3f(GLfloat x, GLfloat
y, GLfloat z);
descrive un punto in tre dimensioni usando i numeri
in virgola mobile. Se invece líinformazione è memorizzata
in un vettore
GLfloat vertex[3]
possiamo usare il comando
glVertex3fv(vertex);
I vertici possono definire uníampia varietà
di oggetti geometrici, e un diverso numero di vertici risulta
necessario, a seconda dellíoggetto geometrico da rappresentare.
Possiamo raggruppare quanti vertici vogliamo usando le funzioni
glBegin e
glEnd. Líargomento
di glBegin
specifica la figura geometrica che vogliamo che i nostri vertici
definiscano. Ad esempio, per specificare un triangolo con vertici
nei punti di coordinate (0, 0, 0), (0, 1, 0)
e (1, 0, 1) si potrebbe scrivere:
glBegin(GL_POLYGON);glVertex3i(0,
0, 0);glVertex3i(0, 1, 0);glVertex3i(1, 0, 1);glEnd();
Tra la coppia di comandi glBegin e glEnd possono naturalmente trovarsi altre istruzioni o chiamate di funzioni. Ad esempio si possono modificare gli attributi oppure eseguire dei calcoli per determinare il vertice successivo.
I possibili oggetti geometrici, tutti definibili
in termini di vertici o segmenti di linea, messi a disposizione
da OpenGL sono riassunti nella tabella 3.1. Presi complessivamente,
questi tipi di oggetto soddisfano le necessità di quasi
tutte le applicazioni grafiche. Naturalmente anche un segmento
di linea è specificato da una coppia di vertici, ma esso
risulta talmente importante da essere considerato quale uníentità
geometrica di base. I segmenti possono essere usati per approssimare
curve, per connettere valori di un grafico, come lati di poligoni.
| GL_POINTSGL_POINTS | ogni vertice descrive la locazione di un punto. |
| GL_LINESGL_LINES | ogni coppia di vertici descrive un segmento di linea. |
| GL_LINE_STRIPGL_LINE_STRIP | serie di segmenti di linea connessi: ogni vertice dopo il primo è un estremo del segmento successivo. |
| GL_LINE_LOOPGL_LINE_LOOP | è come il line strip, ma un segmento viene aggiunto tra il vertice finale ed il vertice iniziale. |
| GL_POLYGONGL_POLYGON | line loop formato da vertici che descrive il contorno di un poligono convesso. |
| GL_TRIANGLEGL_TRIANGLE | ogni triade di vertici consecutivi descrive un triangolo. |
| GL_QUADGL_QUAD | ogni gruppo consecutivo di quattro vertici descrive un quadrilatero. |
| GL_TRIANGLE_STRIPGL_TRIANGLE_STRIP | ogni vertice, ad eccezione dei primi due, descrive un triangolo formato da quel vertice e dai due precedenti. |
| GL_QUAD_STRIPGL_QUAD_STRIP | ogni coppia di vertici, ad eccezione dei primi due, descrive un quadrilatero formato da quella coppia e dalla coppia precedente. |
| GL_TRIANGLE_FANGL_TRIANGLE_FAN | ogni vertice, ad eccezione dei primi due, descrive un triangolo formato da quel vertice e dal vertice precedente e dal primo vertice. |
Come risulta da questa tabella, ci sono più scelte per la visualizzazione delle primitive geometriche. Ad esempio per i segmenti di linea ci sono il tipo GL_LINES, che interpreta ogni coppia di vertici come estremi di un segmento; il tipo GL_LINE_STRIP che consente di connettere i segmenti successivi; ed infine il tipo GL_LINE_LOOP che aggiunge un segmento di linea tra il primo e líultimo vertice.
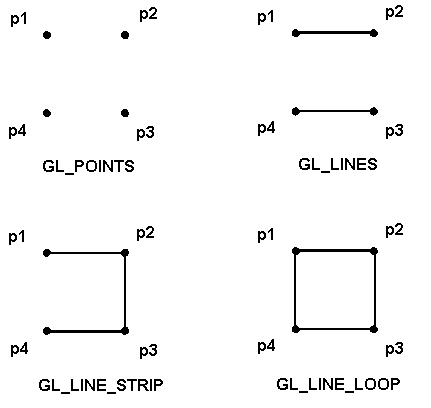 Figura 3.4 Tipi
di segmenti di linea
Figura 3.4 Tipi
di segmenti di lineaUna delle differenze concettuali più importanti tra i tipi di oggetto è se essi abbiano o meno una regione interna. Usualmente il termine poligono è riservato agli oggetti chiusi, come quelli ottenibili con il tipo LINE_LOOP, ma dotati di regione interna. » possibile visualizzare un poligono in diversi modi. Ad esempio si possono visualizzare solo i suoi lati. Oppure possiamo riempire la regione interna con un colore, o con un pattern, e i lati possono essere visualizzati oppure no. Nonostante i lati di un poligono siano facilmente definibili tramite una lista di vertici, se la regione interna non è ben definita, il rendering del poligono può risultare scorretto. Di conseguenza è necessario stabilire come poter definire la regione interna di un poligono.
In due dimensioni, fino a quando nessuna coppia di lati si interseca, abbiamo un poligono semplice, con una regione interna chiaramente definita. Dunque le locazioni dei vertici determinano se il poligono è semplice oppure no.
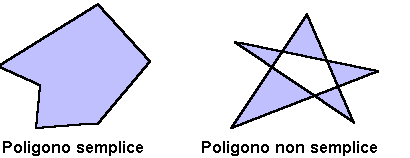 Figura 3.5 Poligoni
semplici e non semplici.
Figura 3.5 Poligoni
semplici e non semplici.» possibile definire una regione interna anche per i poligoni non semplici, in modo che líalgoritmo di rendering possa riempire qualsiasi tipo di poligono. Gli algoritmi di riempimento dei poligoni sono basati sullíelaborazione di punti allíinterno dei poligono, a ciascuno dei quali viene assegnato un particolare colore. Ci sono diversi test che possono essere utilizzati per determinare se un punto sia da considerare interno o esterno al poligono. Uno dei più applicati è il cosiddetto odd-even test. Líidea di base è fondata sulla considerazione che se un punto è nella regione interna del poligono, allora un raggio che si emana da esso in direzione dellíinfinito, deve attraversare un numero dispari di lati del poligono, mentre per i punti allíesterno, i raggi emanati devono attraversare un numero pari di lati per raggiungere líinfinito. Questo test è facile da implementare e si integra bene con i processi standard di rendering.
Sebbene il test pari-dispari sua semplice da implementare e si integri bene nel processo di rendering standard, a volte si desidera un algoritmo che riempia interamente un poligono a stella come quello della Figura 3.4. Líalgoritmo di winding considera di percorrere i lati del poligono da un vertice qualunque in una direzione qualunque fino a raggiungere il punto di partenza. Per ciascun punto si considera una linea arbitaria infinita e si calcola il numero di winding per quel punto come il numero di lati che tagliano la linea in direzione verso il basso meno il numero di lati che tagliano la linea verso líalto. Se il numero di winding non Ë zero, il punto Ë interno al poligono. Il linguaggio PostScript utilizza questo algoritmo di riempimento.
Una ragione per preferire il test pari-dispari Ë che líeffetto di riempimento non cambia a seconda di quali vertici sono usati per indicare il poligono, ad esempio:
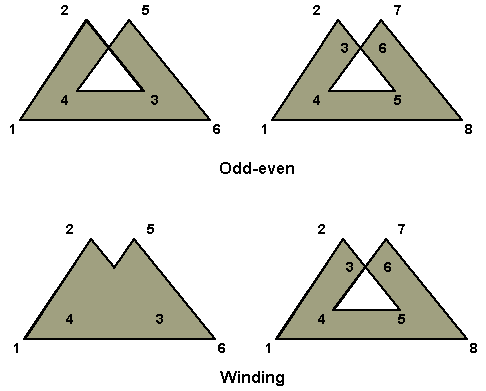 Figura 3.6 Riempimento
di poligoni non semplici
Figura 3.6 Riempimento
di poligoni non sempliciUn oggetto si definisce convesso se tutti i punti su un segmento di linea che congiunge due punti al suo interno, o sul suo bordo, si trovano allíinterno dellíoggetto. Anche per la convessità ci sono appositi test. Nel caso bidimensionale (la definizione di convessità si estende a qualunque dimensione) se un punto è allíinterno del poligono, e ne tracciamo il contorno in senso orario, il punto deve rimanere sulla destra di ciascun lato del contorno.
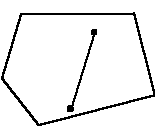 Figura 3.7 Poligono
convesso.
Figura 3.7 Poligono
convesso.Molte librerie grafiche garantiscono un corretto riempimento delle figure geometriche solo quando queste sono convesse. In particolare OpenGL richiede che i poligoni siano semplici, convessi e senza buchi: nel caso queste condizioni non siano rispettate, non Ë assicurata una visualizzazione corretta. Figure complesse che richiedono poligoni con queste propriet‡ si ottengono formando líunione di poligoni semplici convessi, come fanno alcune delle funzioni della libreria GLUT.
In tre dimensioni si presenta qualche difficoltà in più poiché le figure possono non essere piane. Se un poligono non Ë planare, per effetto di trasformazioni, ad esempio una proiezione, si puÚ ottenere un poligono non semplice. Molti sistemi grafici sfruttano la propriet‡ che tre vertici non allineati determinano sia un triangolo che il piano in cui giace il triangolo. Quindi, usando sempre i triangoli è possibile garantire un rendering corretto degli oggetti.
Tornando ai diversi tipi di OpenGL illustrati in tabella 3.1, per le figure con regione interna abbiamo queste possibilità. Il tipo GL_POLYGON produce la stessa figura che si ottiene usando LINE_LOOP: i vertici successivi definiscono i segmenti di linea, e un segmento connette il primo e líultimo vertice. Il riempimento della regione interna del poligono è determinato dagli attributi, che consentono inoltre di specificare se visualizzare o meno i lati. I tipi GL_TRIANGLES e GL_QUADS sono casi speciali di poligoni: gruppi successivi di tre e quattro vertici sono interpretati come triangoli e quadrilateri, rispettivamente. Líuso di questi tipi consente un rendering più efficiente di quello ottenibile con GL_POLYGON.
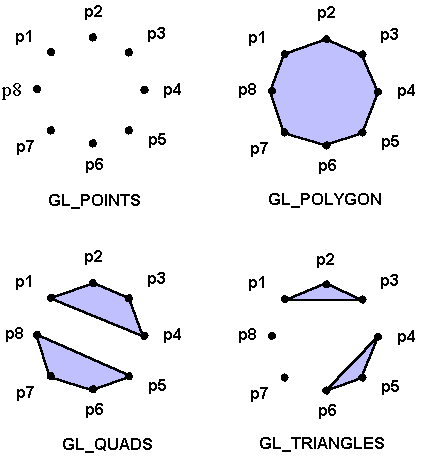 Figura 3.5 Figura
3.8 Tipi di poligoni
Figura 3.5 Figura
3.8 Tipi di poligoniI tipi GL_TRIANGLE_STRIP, GL_QUAD_STRIP, GL_TRIANGLE_FAN sono invece basati su gruppi di triangoli e quadrilateri che condividono vertici ed archi. Col tipo TRIANGLE_STRIP, ad esempio, ogni vertice addizionale aggiunge un nuovo triangolo (figura 3.6).
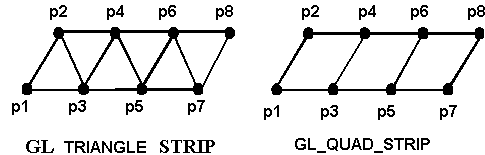 Figura 3.9 Tipi
Triangle_strip e Quad_strip
Figura 3.9 Tipi
Triangle_strip e Quad_stripIn diverse applicazioni gli output grafici sono accompagnati da annotazioni testuali. Nonostante gli output testuali siano la norma nei programmi non grafici, i testi in computer graphics risultano più problematici da gestire. Infatti, mentre nelle applicazioni non grafiche ci si accontenta di un solo insieme di caratteri, visualizzati sempre nella stesso modo, nella computer graphics si desidera controllare stile, font, dimensione, colore ed altri parametri.
Ci sono due forme di testo: stroke e raster. I testi stroke sono costruiti esattamente come le altre primitive grafiche. Si usano vertici, segmenti di linee e curve per descrivere il contorno dei caratteri. Il vantaggio principale dei testi stroke è una conseguenza diretta della loro definizione: dato che i caratteri sono descritti nello stesso modo degli altri oggetti geometrici, è possibile raggiungere un notevole livello di dettaglio nella loro rappresentazione. » inoltre possibile manipolarli attraverso le trasformazioni standard, e visualizzarli come qualsiasi altra primitiva grafica. Un altro vantaggio dei testi stroke è che rendendo un carattere più grosso o più piccolo, esso mantiene dettagli e aspetto; di conseguenza è necessario definire i caratteri una sola volta e usare le trasformazioni per generarli con la dimensione e líorientazione desiderate. La definizione di una famiglia di 128 o 256 caratteri di un determinato stile (font) può tuttavia risultare complessa e richiedere una porzione di memoria ed un tempo di elaborazione significativi.
I testi di tipo raster sono più semplici e veloci. I caratteri sono definiti come rettangoli di bit, chiamati bitblock, e ogni blocco definisce un singolo carattere attraverso un opportuno pattern di 0 e di 1. Un carattere raster può essere posto nel frame buffer attraverso uníoperazione di trasferimento che muove ogni bitblock con una singola istruzione. Alcune trasformazioni dei caratteri raster, ad esempio le rotazioni, possono tuttavia perdere significato in quanto i bit che definiscono il carattere possono finire in locazioni che non corrispondono alle locazioni dei pixel nel frame buffer. Inoltre, dato che i caratteri raster sono spesso memorizzati in memorie ROM (read only memory) nellíhardware, alcuni font possono risultare di portabilità limitata.
Tutte le primitive del nostro set di base sono definite attraverso i vertici. Ad eccezione del tipo point, tutti gli altri tipi consistono di segmenti di linea, o usano i segmenti di linea per definire contorni di altre figure geometriche. » comunque possibile arricchire ulteriormente il set di oggetti.
Per prima cosa, si possono usare le primitive disponibili per approssimare curve e superfici. Ad esempio un cerchio può essere approssimato attraverso un poligono regolare di n lati; nello stesso modo, una sfera può essere approssimata con un poliedro.
Un approccio alternativo è quello di partire dalle definizioni matematiche degli oggetti curvilinei, e quindi di costruire funzioni grafiche per implementarle. Oggetti quali superfici quadriche, curve polinomiali parametriche, e superfici hanno una chiara definizione matematica, e possono essere specificati attraverso opportuni insiemi di vertici. Ad esempio, una sfera può essere definita dal suo centro e da un punto sulla sua superficie.
Quasi tutti i sistemi grafici consentono di seguire entrambi gli approcci. In OpenGL possiamo usare la libreria GLU che mette a disposizione una collezione di approssimazioni di curve e superfici comuni, e possiamo anche scrivere nuove funzioni per definire altre figure.
In un sistema grafico moderno vi è una distinzione tra il tipo di primitiva e la sua visualizzazione. Una linea tratteggiata, ad esempio, ed una linea continua sono dello stesso tipo geometrico, ma sono visualizzate diversamente. Si definisce attributo qualsiasi proprietà che determina come una primitiva geometrica deve essere visualizzata. Il colore è un attributo ovvio, così come lo spessore delle linee ed il pattern usato per riempire i poligoni.
Ad ogni attributo Ë associato un valore corrente,
il quale puÚ essere modificato con apposite funzioni di
modifica. Il valore corrente di un attributo si applica a tutte
le operazioni che seguono, fino alla successiva modifica. Inizialmente
gli attributi hanno ciascuno un proprio valore di default.
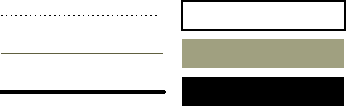 Figura 3.10 Alcuni
attributi per linee e poligoni.
Figura 3.10 Alcuni
attributi per linee e poligoni.Gli attributi possono essere associati alle primitive in diversi punti del processing pipeline. Nel modo immediato, le primitive non sono memorizzate nel sistema, ma vengono visualizzate non appena sono state definite. I valori attuali degli attributi sono parte dello stato del sistema grafico. Nel sistema non rimane dunque memoria della primitiva; solo líimmagine appare sul display, e una volta cancellata dal display, la primitiva è persa. Le display list consentono invece di mantenere oggetti nella memoria, in modo che essi possano essere visualizzati nuovamente.
Ad ogni tipo geometrico è associato un certo
insieme di attributi. Un punto prevede attributi per il colore
e la dimensione. Ad esempio, la dimensione può essere posta
uguale a due pixel usando il comando
glPointSize(2.0);
Un segmento lineare può avere un colore, uno
spessore, che si imposta con:
void glLineWidth(Glfloat
size)
ed un tipo di tratto (continuo, tratteggiato, punteggiato),
che si imposta con:
void glLineStipple(Glint
factor, Glushort pattern)
dove pattern Ë costituito da 16 bit che rappresentano il tratto, e factor il fattore di scala.
Le primitive dei poligoni hanno più attributi,
poiché si deve specificare il riempimento delle regioni
interne: possiamo usare un a tinta unita, o un pattern, possiamo
decidere se riempire o meno il poligono, se visualizzare o meno
il suo contorno. Il tipo di rendering dei poligoni si determina
con la primitiva:
void glPolygonMode(Glenum
face, Glenum mode)
dove face puÚ essere GL_FRONT (solo la faccia di fronte), GL_BACK (solo la faccia posteriore), GL_FRONT_AND_BACK (entrambe le facce), mentre mode puÚ essere GL_POINT (solo i vertici), GL_LINE (solo i lati) o GL_FILL (riempimento della parte interna).
Nei sistemi in cui si utilizzano i testi stroke come primitive, esistono attributi anche per la direzione della stringa di testo, líaltezza e la larghezza dei caratteri, il font e lo stile (italico, neretto, sottolineato).
Si osservi infine che gli attributi relativi alla dimensione dei punti e alla larghezza delle linee sono specificati in termini di dimensione dei pixel. Pertanto, se due display hanno pixel di dimensione differente, líimmagine visualizzata può apparire leggermente diversa. Alcune librerie grafiche, nel tentativo di assicurare che immagini identiche siano prodotte su tutti i sistemi, specificano gli attributi in modo indipendente dal dispositivo di output. Sfortunatamente, assicurare che due sistemi producano lo stesso output grafico costituisce un problema di difficile risoluzione.
Ci sono diverse tecniche per la visualizzazione del colore. Nel sistema RGB, ogni pixel ha componenti separate per i tre colori, un byte per ciascuno. Dato che la libreria grafica deve essere il più possibile indipendente dal sistema hardware, è importante avere la possibilità di specificare il colore indipendentemente del numero di bit nel frame buffer, e lasciare allíhardware del sistema il compito di approssimare il colore richiesto nel miglior modo possibile, compatibilmente con il display disponibile.
Una tecnica molto diffusa è quella basata
sul cosiddetto color cube: le componenti
di colore vengono specificate tramite i numeri compresi tra 0.0
e 1.0, dove 1.0 denota il valore massimo del corrispondente colore
primario, e 0.0 il valore nullo. In OpenGL il color cube si implementa
nel modo seguente. Per disegnare usando, ad esempio, il colore
rosso si chiama la funzione
glColor3f(1.0,
0.0, 0.0);
Poiché il colore fa parte dello stato, si continuerà a disegnare in rosso fino a quando il colore viene cambiato. La stringa ì3fî è usata per indicare che il colore è specificato in accordo al modello RGB a tre colori, e che i valori delle componenti di colore sono in virgola mobile. Se si fa riferimento al sistema RGBA, si utilizza il valore alpha come indice per líopacità o la trasparenza (un oggetto opaco è un oggetto attraverso cui non passa la luce, mentre un oggetto è trasparente se lascia passare la luce).
Uno dei primi compiti che devono essere eseguiti
in un programma è quello di ripulire líarea dello
schermo ñ la drawing window ñ destinata alla visualizzazione
dellíoutput; e questa operazione deve essere ripetuta ogni
volta che si deve visualizzare una nuova immagine. Usando il sistema
di colorazione a quattro dimensioni (RGBA) possiamo creare effetti
in cui le drawing window possono intersecarsi con altre finestre,
manipolando il valore dellíopacità. La chiamata
della funzione
glClearColor(1.0,
1.0, 1.0, 0.0);
definisce un clearing bianco, poiché
le prime tre componenti sono uguali a 1.0, ed opaco, poiché
la componente alpha è pari a 0.0. Quando invece si utilizza
il sistema di colorazione basato sulle tabelle look-up, i colori
vengono selezionati attraverso la funzione
glIndexi(element);
che seleziona un particolare colore dalla tabella.
Per quanto riguarda il setting degli attributi di
colore, quando si usa il sistema RGB, ci sono tre attributi da
definire. Il primo è il colore di clear, che è
definito dal comando
glClearColor(1.0,
1.0, 1.0, 0.0);
Il colore di rendering per i punti che visualizzeremo
può essere selezionato attraverso la chiamata della funzione
glColor3f(1.0, 0.0, 0.0);
che, in questo esempio, è relativa al colore rosso.
Siamo ora in grado di disporre uníampia varietà di informazioni grafiche sul nostro schermo bidimensionale, e siamo anche in grado di descrivere come vorremmo che questi oggetti vengano visualizzati. Tuttavia ancora non abbiamo un metodo per specificare esattamente quali di questi oggetti devono apparire sullo schermo.
La visualizzazione in due dimensioni consiste nel
prendere uníarea rettangolare sul nostro mondo bidimensionale
e nel trasferire il suo contenuto sul display. Líarea del
mondo che visualizziamo è chiamata rettangolo di visualizzazione
o rettangolo di clipping.
Gli oggetti allíinterno del rettangolo saranno nellíimmagine
visualizzata; gli oggetti al di fuori saranno tagliati fuori;
gli oggetti a cavallo dei lati del rettangolo risulteranno parzialmente
visibili (figura 3.9). La dimensione della finestra e la posizione
in cui la finestra deve apparire sullo schermo sono due decisioni
indipendenti, che vengono gestite attraverso le funzioni di controllo.
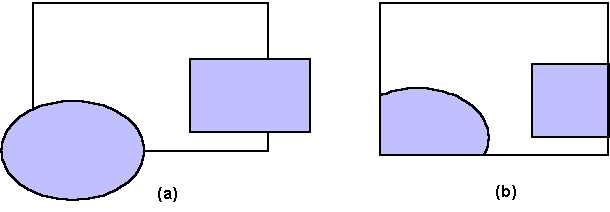 Figura 3.11 Visualizzazione
bidimensionale
Figura 3.11 Visualizzazione
bidimensionale Poiché la grafica bidimensionale è un caso particolare della grafica tridimensionale, possiamo considerare il nostro rettangolo di visualizzazione disposto sul piano z = 0 allíinterno di un volume tridimensionale di visualizzazione. Se non specifichiamo un volume di visualizzazione, OpenGL usa il suo cubo 2 2 2 di default, con origine nel centro. In termini del nostro piano bidimensionale, il vertice in basso a sinistra giace nel punto di coordinate (ñ1.0, ñ1.0), e il vertice in alto a destra nel punto (1.0, 1.0).
La visualizzazione bidimensionale descritta rappresenta un caso speciale di proiezione ortografica. Una proiezione ortografica consiste nel proiettare il punto (x, y, z) sul punto (x, y, 0). Dato che il nostro mondo bidimensionale consiste del solo piano z = 0, la proiezione non ha alcun effetto; tuttavia le proiezioni consentono di impiegare le tecniche dei sistemi grafici tridimensionali per produrre le immagini.
Nella libreria OpenGL, una proiezione ortografica
con un volume di visualizzazione formato da un parallelepipedo
retto è specifica tramite il comando
void glOrtho(GLdouble
left, GLdouble right, GLdouble bottom,GLdouble
top, GLdouble near, GLdouble far)
Fino a quando il piano z = 0 è
posizionato tra near
e far, il
piano bidimensionale interseca il volume di visualizzazione. Se
invece il fatto di fare riferimento ad un volume tridimensionale
in uníapplicazione bidimensionale può sembrare strano,
si può utilizzare la funzione
void glOrtho2D(GLdouble
left, GLdouble right, GLdouble bottom, GLdouble
top)
della libreria GLU, che consente di rendere il programma più leggibile. Questa funzione è equivalente a glOrtho, dove a near e far sono attribuiti i valori ñ1.0 e 1.0, rispettivamente.
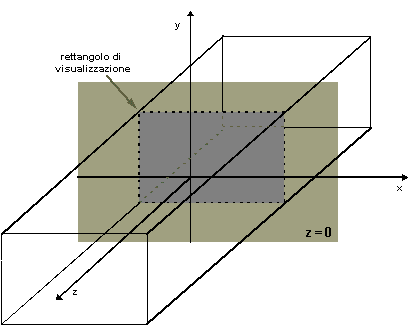 Figura 3.12 Volume
di visualizzazione
Figura 3.12 Volume
di visualizzazione
 Figura 3.13 Proiezione
ortografica
Figura 3.13 Proiezione
ortograficaNei sistemi grafici líimmagine desiderata di una primitiva si ottiene moltiplicando, o concatenando, un certo numero di matrici di trasformazione. Come la maggior parte delle variabili di OpenGL, i valori di queste matrici fanno parte dello stato del sistema, e rimangono validi fino a quando non sono cambiati. Le due matrici più importanti sono la matrice model-view e la matrice proiezione. OpenGL contiene delle funzioni che hanno proprio il compito di manipolare queste matrici. Tipicamente si parte da una matrici identica che viene successivamente modificata applicando una sequenza di trasformazioni. La funzione matrix mode si usa per indicare la matrice a cui le operazioni devono essere applicate. Per default, le operazioni vengono applicate alla matrice model-view.
La seguente sequenza di istruzioni è comunemente
utilizzata per predisporre un rettangolo di visualizzazione bidimensionale:
glMatrixMode(GL_PROJECTION);glLoadIdentity();glOrtho2D(0.0,
500.0, 0.0, 500.0);glMatrixMode(GL_MODELVIEW);
Questa sequenza definisce un rettangolo di visualizzazione 500 500, con il vertice in basso a sinistra posto nellíorigine del sistema bidimensionale. Nei programmi complessi, è sempre utile restituire il matrix mode, nellíesempio model-view, per evitare i problemi che si potrebbero verificare perdendo traccia del matrix mode in cui il programma si trova ad un certo istante.
Le funzioni di controllo gestiscono le interazioni del sistema grafico con il sistema window ed il sistema operativo. La libreria OpenGL Utility Toolkit (in breve GLUT) fornisce una semplice interfaccia tra il sistema grafico e i sistemi window e operativo.
Utilizzeremo il termine finestra (window) per indicare uníarea rettangolare del display che, per default, sarà lo schermo di un CRT. Dato che nei display di tipo raster si visualizza il contenuto del frame buffer, ampiezza e líaltezza della finestra sono misurate in pixel. Si noti che in OpenGL le coordinate della finestra sono tridimensionali, mentre quelle dello schermo sono bidimensionali.
Utilizzeremo invece il termine sistema window per fare riferimento agli ambienti multiwindow, forniti da sistemi come X Window e Microsoft Windows, che consentono di aprire più finestre contemporaneamente sullo schermo di un CRT. Ogni finestra può avere finalità differenti, dallíediting di un file al monitoraggio del sistema.
Per il sistema window, la finestra grafica è un particolare tipo di finestra ñ una in cui la grafica può essere visualizzata ñ gestito dal sistema. Le posizioni nella finestra grafica sono misurate rispetto ad uno dei suoi angoli. Di solito si sceglie líangolo in basso a sinistra come origine. Tuttavia, tutti i sistemi grafici visualizzano le schermo così come i sistemi televisivi, dallíalto al basso e da sinistra verso destra. In questo caso líangolo in alto a sinistra dovrebbe essere líorigine. Nei comandi OpenGL si assume che líorigine sia in basso a sinistra, ma líinformazione restituita al sistema di windowing, ad esempio la posizione del mouse, ha di solito come origine líangolo in alto a sinistra.
Prima di aprire una finestra, ci deve essere interazione
tra il sistema window e OpenGL. Nella libreria GLUT, questa interazione
è avviata dalla chiamata della funzione
glutInit(int *argcp,
char **argv);
i cui argomenti sono simili a quelli della funzione
main del
linguaggio C. Possiamo quindi aprire una finestra chiamando la
funzione GLUT
glutCreateWindow(char
*name)
dove il titolo della finestra è dato dalla stringa name.
La finestra creata avrà di default una dimensione,
una posizione sullo schermo e alcune caratteristiche quali líuso
del sistema di colorazione RGB. Possiamo comunque usare le funzioni
della libreria GLUT per specificare questi parametri prima di
creare la finestra. Ad esempio il codice
glutInitDisplayMode(GLUT_RGB
| GLUT_DEPTH | GLUT_DOUBLE);glutInitWindowSize(640,
480);glutInitWindowPosition(0, 0);
specifica una finestra di dimensione 640 480 nellíangolo in alto a sinistra del display, in cui si usa il sistema di colorazione RGB anziché i colori indicizzati (GLUT_INDEX); un depth buffer per la rimozione delle superfici nascoste, e un double buffering (GLUT_DOUBLE) piuttosto che single (GLUT_SINGLE). Non è necessario specificare queste opzioni in modo esplicito, ma la loro indicazione rende il codice più chiaro. Si osservi infine che nella chiamata di glutInitDisplayMode, si effettua un OR logico dei parametri.
Líaspect-ratio di un rettangolo è definito dal rapporto tra la sua altezza e la sua larghezza. Se líaspect-ratio del rettangolo di visualizzazione, specificato nel comando glOrtho, non è uguale a quello della finestra di output grafico specificata nel comando glutInitWindowSize, si possono verificare effetti indesiderati: gli oggetti possono infatti risultare distorti sullo schermo. Infatti, per trasferire tutto il contenuto del rettangolo di visualizzazione sulla finestra di display si è costretti a distorcerne il contenuto. La distorsione può invece essere evitata facendo in modo che rettangolo di visualizzazione e finestra di display abbiano lo stesso aspect-ratio.
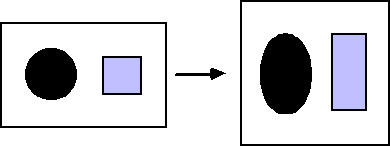 Figura 3.14 Distorsione
delle immagini dovuta a aspect-ratio differenti
Figura 3.14 Distorsione
delle immagini dovuta a aspect-ratio differenti
Un altro metodo più flessibile è quello
di usare il viewport (spioncino). Un viewport
è uníarea rettangolare della finestra di display.
Per default è líintera finestra, ma si può
scegliere una qualsiasi dimensione utilizzando il comando
void glViewport(GLint
x, GLint y, GLsizei w, GLsizei h)
dove (x, y) è líangolo in basso a sinistra del viewport (misurato rispetto allíangolo in basso a sinistra della finestra), e w e h definiscono larghezza e altezza del viewport. I dati, rappresentati da numeri interi, permettono di specificare posizioni e distanze in pixel. Le primitive sono visualizzate nel viewport, e líaltezza e la larghezza del viewport possono essere definite in modo da ottenere lo stesso aspect-ratio del rettangolo di visualizzazione, per evitare il problema della distorsione delle immagini. » inoltre possibile utilizzare più viewport per disporre immagini differenti in parti differenti dello schermo.
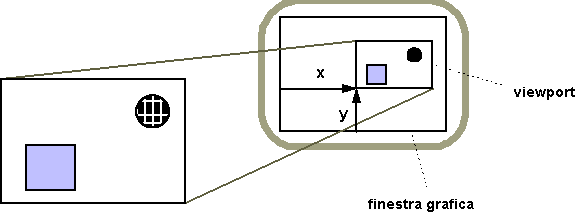 Figura 3.15 Mapping
del rettangolo di visualizzazione sul viewport
Figura 3.15 Mapping
del rettangolo di visualizzazione sul viewport
Potremmo pensare che il nostro programma, una volta
effettuata líinizializzazione di GLUT e degli attributi,
potrebbe passare a disegnare direttamente líimmagine che
ci interessa. Quando si lavora in modalit‡ grafica immediata,
le primitive infatti vengono rese sullo schermo non appena invocate.
Tuttavia, se usiamo un sistema a finestre, questo non basta, perchÈ
la finestra puÚ venire nascosta da altre finestre e quando
verr‡ riesposta líimmagine dovr‡ essere ridisegnata.
Quindi occorre che il disegno del contenuto della finestra venga
svolto ogni volta che accade un evento nel sistema a finestre
che lo rende necessario. Questo si ottiene passando il controllo
ad un event-loop che esamina gli eventi del sistema a finestre
e li gestisce, realizzato dalla procedura:
void glutMainLoop(void)
Per informare líevent-loop di come deve essere
ridisegnato il contenuto di una finestra OpenGL, dobbiamo passargli
la funzione che dovr‡ utilizzare, tramite la procedura GLUT:
void glutDisplayFunc(void
(*func)(void))
Naturalmente la chiamata a questa procedura va fatta
prima di eseguire glutMainLoop.
PoichÈ uníapplicazione non interattiva non deve
far altro che passare il controllo allíevent-loop, molto
spesso puÚ essere realizzata secondo lo schema di programma
che segue. Allíinizio sono inseriti i comandi per líinclusione
degli header file per OpenGL e GLUT. Per predisporre le variabili
di stato relative alla visualizzazione e agli attributi (parametri
che si vogliono scegliere in modo indipendente della funzioni
di visualizzazione), si definisce una procedura a parte: myinit().
#include <GL/gl.h>#include
<GL/glut.h>
void main(int argc, char** argv){void myinit(), display();
glutInit(&argc,argv);glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);glutInitWindowSize(500,
500);glutInitWindowPosition(0, 0);glutCreateWindow(ìsimple
OpenGL exampleî);glutDisplayFunc(display);myinit();glutMainLoop();}
Come esempio di applicazione della libreria grafica OpenGL, vediamo come disegnare il Sierpinsky Gasket, una forma geometrica di un certo interesse in aree come quella della geometria dei frattali. Il Sierpinsky Gasket è un oggetto che può essere definito ricorsivamente e casualmente, ma le cui proprietà finali sono niente affatto casuali.
Supponiamo di partire da tre vertici nel piano, le
cui locazioni, specificate rispetto ad un opportuno sistema di
coordinate, siano (x1, y1),
(x2, y2) e (x3, y3).
La costruzione procede nel seguente modo:
Dunque, i punti vengono immediatamente visualizzati sul dispositivo di output, non appena sono stati generati.
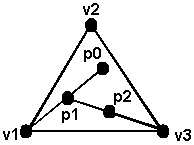 Figura 3.16 Generazione
del Sierpinsky Gasket
Figura 3.16 Generazione
del Sierpinsky Gasket
Il programma OpenGL per la generazione del Sierpinsky
Gasket è piuttosto semplice. Il programma main
viene completato scrivendo le funzioni myinit
e display.
Disegneremo punti rossi su uno sfondo bianco. Inoltre, il sistema
di coordinate è definito in modo tale che i punti siano
presi entro un quadrato 500 500 con origine nellíangolo
in basso a sinistra.
/* This program computes 5000
points in response to display callback issued when window opened.
After computing points program sits in wait loop */
#include <GL/gl.h>#include <GL/glut.h>
void myinit(void){/* attributes */glClearColor(1.0,1.0,1.0,0.0);
/* white background */glColor3f(1.0,0.0,0.0); /* draw in red
*/
/* set up viewing *//* 500 x 500 window with origin lower left
*/
glMatrixMode(GL_PROJECTION);glLoadIdentity();glOrtho2D(0.0,500.0,0.0,500.0);glMatrixMode(GL_MODELVIEW);}
void display(void){/* define a point data type */
typedef GLfloat point2[2];point2 vertices[3]={{0.0,0.0},{250.0,500.0},{500.0,0.0}};
/* an arbitrary triangle */
int i, j, k;long random(); /* standard random number generator
*/point2 p={75.0,50.0}; /* an arbitrary initial point */
glClear(GL_COLOR_BUFFER_BIT); /* clear the window */
/* computes and plots 5000 new points */
for( k = 0; k < 5000; k++){j = random()%3; /* pick a vertex
at random */
/* Compute point halfway between vertex and old point */
p[0] = (p[0] + vertices[j][0]) / 2.0;p[1] = (p[1] + vertices[j][1])
/ 2.0;
/* plot new point */
glBegin(GL_POINTS);glVertex2fv(p);glEnd();}
glFlush(); /* clear buffers */}
void main(int argc, char** argv){glutInit(&argc,argv);glutInitDisplayMode
(GLUT_SINGLE | GLUT_RGB); /* default, non necessario */glutInitWindowSize(500,
500); /* finestra di 500x500 pixel */glutInitWindowPosition(0,
0); /* finestra in alto a sinistra */glutCreateWindow(ìSierpinsky
Gasketî); /* titolo della finestra */glutDisplayFunc(display);
/* display callback invoked when
window opened */myinit(); /* imposta
gli attributi */glutMainLoop(); /* attiva event loop */}
La funzione display definisce al suo interno un triangolo arbitrario e un punto iniziale arbitrario. Inoltre, essa prevede un ciclo per la generazione di 5000 punti, ed una chiamata della funzione glFlush che forza il sistema a visualizzare i punti sul display non appena possibile.
 Figura 3.17 Sierpinsky
Gasket
Figura 3.17 Sierpinsky
GasketIl programma illustrato per il Sierpinsky Gasket può facilmente essere generalizzato al caso tridimensionale. Per ottenere un Sierpinsky Gasket tridimensionale è necessario partire da un tetraedro. Poiché il tetraedro è convesso, il punto medio di un segmento di linea tracciato tra uno dei suoi vertici ed un punto al suo interno, risulta ancora interno al tetraedro. Quindi è possibile seguire la stessa procedura, con la sola differenza che ora avremo bisogno di quattro punti iniziali per definire il tetraedro. Si osservi che possiamo scegliere i quattro punti casualmente, senza influenzare il risultato finale.
Le variazioni sono da apportare soprattutto alla
funzione display.
Si deve definire un point data type tridimensionale:
typedef GLfloat point[3];
e inizializzare i vertici del tetraedro, ad esempio
con il seguente codice
point vertices[4]={{0.0,0.0,0.0},{250.0,500.0,100.0},{500.0,250.0,250.0},{250.0,100.0,250.0}};
point p ={250.0,100.0,250.0}; /* random initial point */
Quindi possiamo usare la funzione glPoint3fv
per visualizzare i punti. La parte centrale della funzione display
diventa
/* Computes and plots a single
new point */
long random();int i;j = random()%4; /* pick
a vertex at random */
/* Compute point halfway between vertex and old point */
p[0] = (p[0] + vertices[j][0])/2.0;p[1] = (p[1] + vertices[j][1])/2.0;p[2]
= (p[2] + vertices[j][2])/2.0;
/* Plot point */
glBegin(GL_POINTS);glColor3f(p[0]/250.0,p[1]/250.0,p[2]/250.0);glVertex3fv(
p );glEnd();
Per definire un volume tridimensionale, si utilizza
infine la funzione
glOrtho(-500.0, 500.0, -500.0,
500.0, -500.0, 500.0);