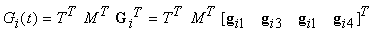.
Le superfici parametriche bicubiche sono una generalizzazione delle curve parametriche cubiche. Si ricordi che la forma generale di una curva cubica parametrica è Q(t)=G M T, dove G, la matrice geometrica, è costante.
Per convenienza di notazione, sostituiamo t con s, quindi scriveremo Q(s)=G M S. Se i punti in G variano nello spazio tridimensionale, seguendo una traiettoria specificata dal parametro t, risulta
Q(s, t) = [G1(t) G2(t). (12.1)
Fissato un valore del parametro, diciamo t1, Q(s, t1) definisce una curva, poiché G(t1) è costante. Sia ora t2 un altro valore del parametro t, molto vicino a t1. Q(s, t2) definisce una curva, solo leggermente diversa da Q(s, t1). Ripetendo questo procedimento molte volte, in corrispondenza di altri valori del parametro compresi tra 0 e 1, si definisce uníintera famiglia di curve, in cui ogni membro è arbitrariamente simile ad uníaltra curva. Líinsieme di tutte queste curve definisce una superficie. Se le Gi(t) sono delle curve cubiche, allora la superficie così definita è detta superficie parametrica bicubica. In questa caso, inoltre, ogni Gi(t) può essere rappresentata nel modo seguente
Gi(t) = Gi M T,
dove Gi = [gi1 gi3 gi1 gi4].
Scrivendo líequazione Gi(t) = Gi M T in forma trasposta (applicando líidentità (ABC)T = CT BT AT) si ottiene
.
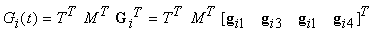
Quindi, sostituendo questo risultato nellíequazione (12.1) per ciascuno dei quattro punti, abbiamo
,
(12.2)
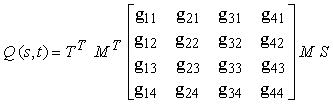
cioè
,
(12.3)
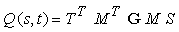
dove 0 s, t 1. Scrivendo líequazione componente per componente, si ottiene infine
(12.4)
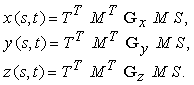
Data questa formulazione generale, si possono poi esaminare dei metodi particolari per specificare le superfici usando matrici geometriche differenti.
Le superfici di Hermite sono completamente definite da una matrice geometrica 4 4 GH. Per derivare la matrice GH si segue lo stesso approccio usato per derivare líequazione (12.3). Vediamo ad esempio come derivare la componente x(s, t). Per prima cosa, si sostituisce t con s nellíequazione x(t) = GHx MH T, che diventa x(s) = GHx MH S. Riscrivendo líespressione in modo tale che la matrice geometrica di Hermite, GHx, non sia più costante, ma una funzione del parametro t, si ottiene
.
(12.5)
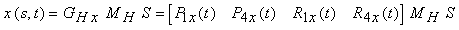
Le funzioni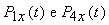 
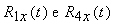
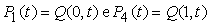
definiscono
la componente x degli estremi della curva nel parametro
s; analogamente, 
rappresentano
i vettori tangenti in questi punti. Ad ogni valore di t,
sono associati i due punti estremi e i due vettori tangenti. La
superficie risulta definita da una interpolazione cubica tra 
,
o, alternativamente tra Q(s, 0) e Q(s,
1).
Nel caso in cui le quattro curve interpolanti Q(0, t) e Q(1, t), Q(s, 0) e Q(s, 1) sono linee rette, il risultato è una superficie rigata. Se le curve interpolanti sono anche complanari, si ottiene un poligono planare a quattro lati.
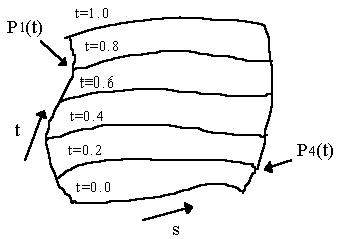Figura 12.1 Linee
di valore parametrico costante su una superficie bicubica. Proseguendo con la derivazione, supponiamo che P1x(t), P4x(t), R1x(t), e R4x(t) siano rappresentate in forma di Hermite:
(12.6)
Le quattro cubiche possono essere riscritte in uníunica equazione
,
(12.7)
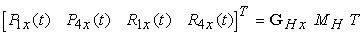
dove
.
(12.8)
Prendendo la trasposta dellíequazione (12.7), si ottiene
.
(12.9)
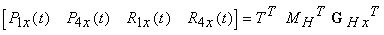
Infine, sostituendo líequazione (12.9) nellíequazione (12.5), risulta
.
(12.10)
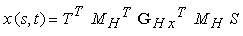
In modo del tutto analogo, si possono derivare le due equazioni
(12.11)
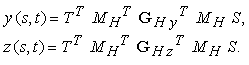
Le matrici GHx, GHy e GHz giocano per le superfici di Hermite lo stesso ruolo giocato dalla matrice GH nel caso delle curve. Inoltre, le superfici bicubiche di Hermite permettono di ottenere una continuità di tipo C1 e G1 tra i vari pezzi di superficie, così come le curve di Hermite permettono una continuità di tipo C1 e G1 tra i vari tratti curvilinei.
La formulazione delle superfici bicubiche di Bèzier può essere derivata seguendo lo stesso procedimento illustrato per le superfici di Hermite, da cui risulta
(12.12)
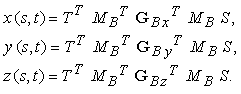
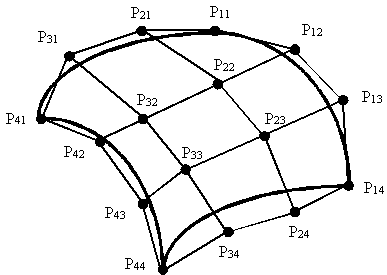
La matrice geometrica di Bézier consiste di 16 punti di controllo, come è mostrato nella Figura 12.2.
Figura
12.2 I sedici punti di controllo di un
pezzo di una superficie di Bézier.Si può ottenere una continuità di tipo C0 e G0 tra le varie parti della superficie facendo coincidere i quattro punti di controllo comuni. La continuità di tipo G1 si ottiene quando i due insiemi di quattro punti di controllo da entrambe le parti del bordo del pezzo di superficie sono allineati con i punti sul bordo stesso.
Le superfici B-splines si possono rappresentare nel seguente modo
(12.13)
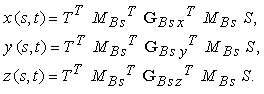
La continuità di tipo C2 è garantita dalle B-splines, senza che sia necessario alcun arrangiamento particolare dei punti di controllo. Líunica cosa importante è evitare la duplicazione di punti di controllo, che può creare delle discontinuità.
Il calcolo del vettore normale ad una superficie bicubica è molto importante. Ad esempio, esso è necessario per implementare le tecniche di shading.
Dallíequazione (12.3), segue che il vettore tangente s alla superficie Q(s, t) è espresso da
,
(12.14)
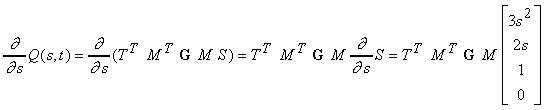
e il vettore t da
.
(12.15)
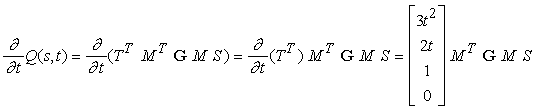
I due vettori tangenti sono paralleli alla superficie nel punto (s,t), quindi il loro prodotto vettoriale risulta perpendicolare alla superficie:
,
(12.16)
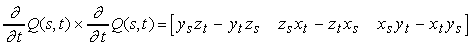
dove abbiamo indicato con xS, yS, zS, e xt, yt, zt, le componenti dei due vettori tangenti.
Si noti che se i vettori tangenti sono uguali a zero, il prodotto vettoriale è nullo e non è possibile definire un vettore normale significativo (un vettore tangente può andare a zero in un punto di giunzione con una continuità di tipo C1, ma non di tipo G1).
Il vettore normale è espresso da un polinomio biquintico, ossia un polinomio in due variabili e di quinto grado. Quindi, calcolare il vettore normale risulta piuttosto costoso dal punto di vista computazionale.
La famiglia delle superfici quadriche è definita dallíequazione implicita
.
(12.17)
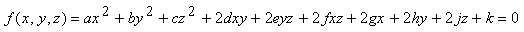
Ad esempio, se a = b = c = -k = 1 e gli altri coefficienti sono uguali a zero, líequazione (12.17) definisce una sfera di raggio unitario con centro nellíorigine. Se i coefficienti da a a f sono uguali a zero, líequazione definisce un piano.
Le superfici quadriche sono utilizzate nelle applicazioni
specializzate, ad esempio nella modellazione di molecole, e sono
state integrate anche in alcune tecniche di modellazione di oggetti
solidi. Altre ragioni per utilizzare le equazioni quadriche in
forma implicita sono la facilità di
;
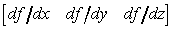OpenGL permette di implementare le curve e le superfici di Bézier attraverso un meccanismo chiamato valutatore, utilizzato per calcolare i valori dei polinomi di Bernstein di ogni ordine. Il valutatore non richiede una spaziatura uniforme dei punti di controllo, ed è uno strumento molto flessibile. Possiamo usare le curve e le superfici di Bézier per generare altri tipi di curve e superfici polinomiali generando nuovi punti di controllo. Il valutatore può essere usato per generare curve e superfici da una fino a quattro dimensioni.
Per le curve, si può definire un valutatore
monodimensionale attraverso la funzione
glMaplf(type, t_min, t_max, stride,
order, point_array);
dove il parametro type specifica il tipo di oggetto che vogliamo valutare usando i polinomi di Bézier; i punti di controllo sono definiti nel vettore puntato da array; i valori t_min e t_max definiscono líintervallo di variazione del parametro; stride rappresenta il numero dei valori del parametro tra i tratti curvilinei; il parametro order, infine, è uguale al grado del polinomio più 1.
Si possono definire anche valutatori multipli, che
sono attivati nello stesso momento e sono usati per valutare,
ad esempio, contemporaneamente curve e normali. Ogni valutatore
deve essere attivato con il comando
glEnable(type);
Una volta che il valutatore è stato predisposto,
possiamo usare la funzione
glEvalCoordlf(t);
tutte le volte che abbiamo bisogno di un valore dal
valutatore attivo. Quindi, glEvalCoordlf
può rimpiazzare ogni combinazione di
glVertex,
glColor e
glNormal,
a seconda di quali valutatori siano stati abilitati. Supponiamo
di avere definito dei valutatori per le curve cubiche di Bézier
sullíintervallo (0,10), e un vettore di punti di controllo.
Possiamo ottenere 100 punti ugualmente spaziati sulla curva nel
seguente modo:
glBegin(GL_LINE_STRIP)for
(i = 0; i < 100; i++) glEvalCoordlf( (float) i / 100.0);glEnd();
Se i valori del parametro sono ugualmente spaziati,
possiamo usare le funzioni
glMapGridlf(100, 0.0, 10.0);glEvalMeshl(GL_LINE,
0, 100);
La prima funzione predispone una griglia uniforme
con cento intervalli, e la seconda genera la curva desiderata.
Le superfici sono generate in modo analogo alle curve. Possiamo
utilizzare le funzioni glMap2
e glEvalCoord2,
ma è necessario specificare due parametri. Per esempio,
una superficie bicubica di Bézier sulla regione (0, 1) (0, 1)
si può ottenere con la funzione
glMap2f(GL_MAP_VERTEX_3, 0.0,
1.0, 3, 4, 0.0, 1.0, 3, 4, data);
Le corrispondenti chiamate delle funzioni valutatore
dipendono dal fatto che si voglia disegnare un mesh, oppure creare
un insieme di poligoni per lo shading. Per il mesh si può
operare in questo modo:
for
(j = 0; j < 100; j++){glBegin(GL_LINE_STRIP);for
(i = 0; i < 100; i++)glEvalCoord2f( (float) i / 100.0,
(float) j / 100.0);glEndg();glBegin(GL_LINE_STRIP);for
(i = 0; i < 100; i++)glEvalCoord2f( (float) j /
100.0, (float) i / 100.0);glEndg();}
Per i quadrilateri, le chiamate di funzioni hanno
la forma seguente:
for
(j = 0; j < 99; j++){glBegin(GL_QUAD_STRIP);for
(i = 0; i < 100; i++)glEvalCoord2f( (float) i / 100.0,
(float) j / 100.0);for (i = 0; i < 100; i++)glEvalCoord2f(
(float) (i+1) / 100.0, (float) j / 100.0);glEndg();}
Per i mesh uniformi, possiamo infine usare i comandi glMapGrid2 e glEvalMesh2.
OpenGL permette anche di implementare alcune quadriche, ad esempio dischi, cilindri e sfere, attraverso líuso della libreria addizionale GLU. Questi oggetti possono essere trattati come un qualsiasi altro oggetto grafico, e quindi scalati, traslati, ruotati e ombreggiati. Líimplementazione di questi oggetti avviene approssimandoli con i poligoni, ed è possibile specificare il numero di poligoni da usare nellíapprossimazione.