 Figura
11.1 Due possibili strutture gerarchiche
per líautomobile.
Figura
11.1 Due possibili strutture gerarchiche
per líautomobile.I modelli sono astrazioni del mondo reale o virtuale. I modelli matematici, utilizzati in molte aree della scienza e dellíingegneria, usano equazioni matematiche per modellare fenomeni fisici. In informatica, si utilizzano i tipi di dati astratti per modellare líorganizzazione degli oggetti. In computer graphics, il mondo viene modellato usando oggetti geometrici.
Quando si costruisce un modello matematico, si deve scegliere attentamente il tipo di matematica che meglio descrive il fenomeno che si desidera rappresentare. In computer graphics si segue un procedimento analogo: si scelgono le primitive da utilizzare e si decide come rappresentare le relazioni che intercorrono tra esse. Spesso ci sono più soluzioni possibili, e in questi casi conviene sempre scegliere il modello che meglio si avvantaggia delle capacità del sistema grafico disponibile.
Ci sono quattro approcci principali allo sviluppo e allíutilizzazione dei modelli. I modelli gerarchici usano un insieme di primitive geometriche molto semplici ed estendono le trasformazioni geometriche per poter rappresentare le relazioni gerarchiche tra gli oggetti. Questa tecnica è particolarmente adatta alle applicazioni come la robotica e líanimazione, applicazioni in cui il comportamento dinamico degli oggetti è caratterizzato da relazioni tra le diverse parti del modello.
Il secondo approccio consiste nel caratterizzare i modelli geometrici attraverso sistemi language-based. Si tratta di modelli grammaticali che danno sia un metodo alternativo per rappresentare le strutture gerarchiche, che un metodo per controllare il livello di dettaglio da raggiungere nella visualizzazione del modello.
Il terzo approccio consiste nellíimposizione di vincoli di natura fisica al modello, e nellíapplicazione di leggi fisiche per governare il comportamento nel tempo degli oggetti geometrici.
Infine, ci sono tecniche che permettono di generare oggetti geometrici a partire da un insieme di dati, e di sfruttare le capacità del sistema grafico per visualizzare gli oggetti geometrici risultanti.
La maggior parte delle librerie grafiche mette a disposizione un insieme limitato di primitive geometriche elementari, e lascia allíutente il compito di costruire oggetti più complessi utilizzando queste primitive. In questo compito, líutente può utilizzare alcune librerie addizionali (come le librerie GLU e GLUT nel caso di OpenGL) che mettono a disposizione altri oggetti geometrici, costruiti usando le primitive della libreria di base. Nellíanalisi seguente faremo líipotesi di avere a disposizione una collezione di oggetti tridimensionali di base, forniti dalle librerie opzionali.
Un approccio non gerarchico alla modellazione consiste
nel considerare gli oggetti geometrici come simboli, ed
il mondo come una collezione di simboli. I simboli, a cui
sono associate una dimensione ed una orientazione, possono essere
modificati applicando le trasformazioni geometriche (rotazioni,
traslazioni e scalature), che consentono di posizionarli nel modello,
con la dimensione e líorientazione desiderate. I programmi
OpenGL contengono spesso ripetizioni di codice della forma:
glMatrixMode(GL_MODELVIEW);glLoadIdentity();glTranslatef();glRotatef();glScalef();glutSolidCylinder();
dove abbiamo considerato come simbolo un cilindro.
I modelli gerarchici rappresentano invece
anche le relazioni tra gli oggetti che costituiscono le varie
parti del modello. Supponiamo ad esempio di volere costruire il
modello di una automobile. Possiamo dividere il modello in cinque
parti, la carrozzeria e le quattro ruote, ciascuna delle quali
sarà descritta usando le primitive di base del sistema
grafico. Per animare líautomobile, possiamo scrivere un
programma che contiene una funzione per generare le ruote e una
funzione per generare la carrozzeria. Queste funzioni ricevono
in input velocità e direzione dellíautomobile, e
líanimazione è realizzata tenendo presente che,
se le ruote hanno raggio r, una rotazione della ruota di
360_ corrisponde ad un movimento dellíautomobile di un
tratto 2pr.
Possiamo dunque scrivere il seguente programma:
main(){float
s=...; /* velocità */float d[3]={...}; /* direzione */draw_right_front_wheel(s,d);draw_left_front_wheel(s,d);draw_right_rear_wheel(s,d);draw_left_rear_wheel(s,d);draw_chassis(s,d);}
Le limitazioni di questo programma sono la sua linearità
ed il fatto che esso non mette in evidenza alcuna delle relazioni
gerarchiche tra le componenti del modello. Ci sono due tipi di
relazioni che sarebbe invece opportuno sfruttare:
Possiamo rappresentare le relazioni gerarchiche tra le parti dei modelli usando i grafi. Dal punto di vista matematico, un grafo è composto da un insieme di nodi e da un insieme di archi, che collegano tra loro coppie di nodi. Agli archi si può associare una direzione, ed in questo caso si dice che il grafo è diretto.
I grafi con cui lavoreremo appartengono alla categoria degli alberi. Un albero è un grafo diretto, privo si cammini chiusi. Ogni nodo, ad eccezione di un nodo detto radice, possiede un arco entrante. Ciò significa che ad ogni nodo, ad eccezione della radice, è associato un nodo padre, che è il nodo da cui parte líarco entrante. Ogni nodo può inoltre avere uno o più nodi figli. Un nodo senza figli è chiamato nodo terminale.
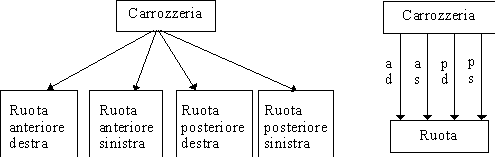
Nellíesempio dellíautomobile, le relazioni gerarchiche tra le componenti possono essere rappresentate dallíalbero mostrato nella Figura 11.1(a), la cui radice corrisponde alla carrozzeria, e i quattro figli alle quattro ruote. Si osservi che nodi e archi possono contenere anche informazioni addizionali. Nel caso dellíautomobile, essi possono ad esempio contenere delle informazioni su come disegnare le componenti. Se vogliamo sfruttare il fatto che le quattro ruote sono identiche possiamo utilizzare una struttura come quella mostrata in figura 11.1 (b), dove si è utilizzato un singolo prototipo per le ruote
 Figura
11.1 Due possibili strutture gerarchiche
per líautomobile.
Figura
11.1 Due possibili strutture gerarchiche
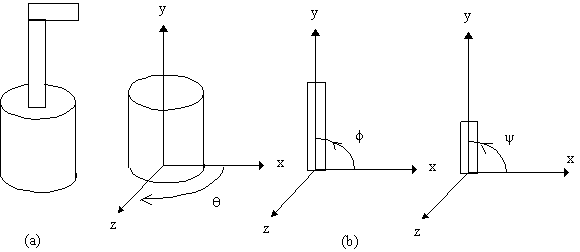
per líautomobile.Esaminiamo adesso due esempi più complessi. Consideriamo per prima cosa il modello di un braccio meccanico, mostrato nella Figura 11.2. Il braccio è composto da tre oggetti geometrici piuttosto semplici, un cilindro e due parallelepipedi, facilmente costruibili con le primitive geometriche di base.
 Figura
11.2 Braccio meccanico. (a) Modello totale.
(b) Componenti.
Figura
11.2 Braccio meccanico. (a) Modello totale.
(b) Componenti.Il meccanismo ha tre gradi di libertà, ciascuno descrivibile da un angolo di giunzione, misurato nel sistema di riferimento della relativa componente. La base può essere ruotata attorno allíasse verticale di un angolo q . Il braccio inferiore del robot è attaccato alla base da una giunzione che gli permette di ruotare nel piano z = 0 del proprio sistema di riferimento. Questa rotazione è specificata dallíangolo f , misurato a partire dallíasse x. Il braccio superiore è attaccato a quello inferiore da una giunzione del tutto simile, e può ruotare di un angolo y , misurato nel proprio sistema di riferimento. Quando gli angoli variano, possiamo pensare che i due sistemi di riferimento si muovano rispetto al sistema di riferimento solidale alla base.
Supponiamo di voler scrivere un programma per animare il robot. Anziché definire le parti del robot ed il loro moto indipendentemente, si può seguire un approccio incrementale. La base del robot può ruotare attorno allíasse y nel proprio sistema, di un angolo q . Quindi, possiamo descrivere il moto di un punto p della base con la matrice di rotazione Ry(). Il braccio inferiore ruota attorno allíasse z del proprio sistema, ma questo sistema deve essere traslato sopra la base, applicando la matrice di traslazione T(0, h1, 0) , dove h1 è líaltezza del punto di giunzione tra la base e il braccio inferiore. Naturalmente, se la base è stata ruotata, dovremo ruotare anche il braccio, applicando la matrice Ry(). Il posizionamento del braccio inferiore può dunque essere eseguito applicando la matrice Ry() T(0, h1, 0) Rz() al suo vertice. Possiamo interpretare la matrice Ry() T(0, h1, 0) come la matrice che posiziona il braccio inferiore rispetto allíambiente esterno, e la matrice Rz() come la matrice che posiziona il braccio inferiore rispetto alla base. Un ragionamento del tutto simile può essere applicato al braccio superiore, che deve essere traslato applicando la matrice T(0, h1, 0) e quindi ruotato applicando Rz(). La matrice che controlla il braccio superiore è dunque Ry() T(0, h1, 0) Rz()T(0, h2, 0) Rz().
La forma della funzione di display in OpenGL è
la seguente:
display(){glRotatef(theta,
0.0, 1.0, 0.0);base();glTranslatef(0.0, h1, 0.0);glRotatef(phi,
0.0, 0.0, 1.0);lower_arm();glTranslatef(0.0, h2, 0.0);glRotatef(psi,
0.0, 0.0, 1.0);upper_arm();}
Si osservi che il posizionamento del braccio meccanico è stato descritto indipendentemente dai dettagli delle parti individuali. Se il posizionamento dei punti di giunzione non viene modificato, possiamo modificare la forma del braccio meccanico cambiando solo le funzioni che disegnano le tre parti. Pertanto è possibile scrivere programmi separati che descrivono le componenti e animano il robot.
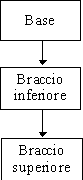
Le relazioni tra le tre componenti del robot sono
mostrate nella Figura 11.3. Ciascun nodo dellíalbero che
rappresenta il robot deve contenere almeno le seguenti informazioni:
Ogni nodo può inoltre includere altre informazioni, ad esempio un insieme di attributi per la sua visualizzazione.
 Figura
11.3 Struttura ad albero del braccio
meccanico.
Figura
11.3 Struttura ad albero del braccio
meccanico.
Per disegnare un oggetto descritto da questo tipo
di struttura, è necessario eseguire una visita dellíalbero:
si deve visitare ogni nodo, e, ad ogni nodo, si deve calcolare
la matrice da applicare alle primitive puntate dal nodo, e infine
visualizzare le primitive.
Consideriamo ora il modello di una figura umana mostrato nella Figura 11.4.
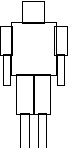 Figura 11.4 Modello
di una figura umana.
Figura 11.4 Modello
di una figura umana.Possiamo rappresentare la figura umana, e le relazione gerarchiche tra le sue parti, con un albero la cui radice corrisponde al torace. Una volta posizionato il torace, orientazione e posizione delle altre parti del modello sono determinate dallíinsieme degli angoli di giunzione. In particolare, definendo il moto degli angoli di giunzione, è possibile animare líintera figura.
Supponiamo di avere a disposizione delle funzioni per disegnare le parti del corpo (simboli) nei propri sistemi di riferimento. Possiamo definire un insieme di nodi per líalbero definendo le matrici che posizionano ciascuna parte relativamente al nodo padre. Ogni matrice è definita dalla concatenazione di una matrice di traslazione e di una matrice di rotazione, e rappresenta la variazione incrementale quando si passa dal nodo padre al nodo figlio. Queste matrici possono essere usate come etichette per gli archi corrispondenti nel grafo (figura 11.5).
Líaspetto interessante messo in evidenza da questo esempio riguarda il modo in cui si deve effettuare la visita dellíalbero. A questo proposito, risulta conveniente seguire líapproccio applicato dagli algoritmi di depth-first search: si parte dalla radice, si segue il ramo più a sinistra fino alla massima profondità consentita, muovendosi sempre verso sinistra, quindi si torna alla radice, ci si sposta di un ramo verso destra, e si procede ricorsivamente. Supponiamo che la funzione figure consenta di disegnare la figura umana. La matrice model-view M, in azione quando la funzione viene invocata, determina la posizione della figura relativamente al resto della scena. Il primo nodo che incontriamo, il torace, viene disegnato applicando la matrice M a tutte le sue primitive.
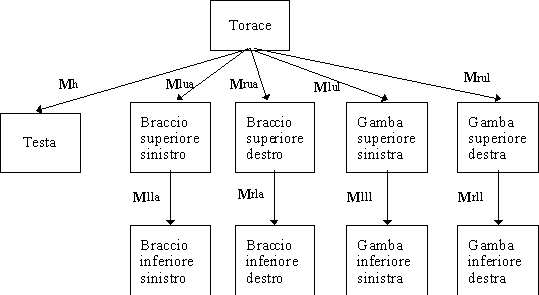 Figura 11.5 Struttura
ad albero della figura umana.
Figura 11.5 Struttura
ad albero della figura umana.
Ci spostiamo poi lungo il ramo di sinistra dellíalbero,
ed incontriamo il nodo relativo alla testa. A questo punto è
necessario invocare la funzione head,
e la matrice model-view deve essere aggiornata, e posta uguale
a MMh. Dato che il nodo relativo alla
testa non ha figli, torniamo alla radice, e procediamo la visita
dellíalbero lungo il ramo corrispondente al braccio sinistro,
disegniamo la parte superiore del braccio applicando la matrice
MMlua, e la parte inferiore applicando
la matrice MMlua MMlla.
Ci muoviamo quindi al braccio destro, alla gamba sinistra e alla
gamba destra. Ogni volta che si raggiunge la profondità
massima dellíalbero, si fa ritorno al nodo radice, e occorre
ripristinare la matrice M come matrice model-view. La matrice
model-view deve quindi essere inizializzata al valore M,
aggiornata a MMh, e successivamente a
MMlua MMlla,
e così via, come mostrato dal seguente codice:
figure(){glPushMatrix();torso();glTranslateglRotate3head();glPopMatrix();glPushMatrix();glTranslateglRotate3left_upper_arm();glPopMatrix();glPushMatrix();glTranslateglRotate3left_lower_arm();glPopMatrix();glPushMatrix();glTranslateglRotate3right_upper_arm();glPopMatrix();glPushMatrix();
Ö
Si osservi come líuso delle funzioni glPushMatrix e glPopMatrix consente di aggiornare e ripristinare efficientemente la matrice model-view. Il primo comando glPushMatrix duplica la matrice model-view corrente (assumendo di avere in precedenza eseguito il comando glMatrixMode(GL_MODELVIEW)), e pone la copia alla testa della pila usata per conservare versioni della matrice model-view che saranno necessarie nel seguito. Líuso della pila consente di lavorare immediatamente con le altre trasformazioni che alterano la matrice model-view. Con le chiamate delle funzioni glTranslate e glRotate si determina Mh e la si concatena alla matrice model-view iniziale. Quindi, si generano le primitive per modellare la testa, e successivamente, con il comando glPopMatrix, si ripristina la matrice model-view iniziale. In modo del tutto analogo si può implementare la gestione degli attributi per la visualizzazione delle diverse parti del corpo. A questo proposito, la libreria OpenGL mette a disposizione dellíutente i comandi glPushAttributes e glPopAttributes, che permettono di trattare gli attributi seguendo la stessa tecnica adottata per la matrice model-view.
I due esempi che abbiamo illustrato, riguardano modelli articolati, costituiti da parti rigide connesse da giunzioni. Possiamo animare questi modelli alterando i valori di un insieme limitato di parametri nel tempo.
Tra i diversi approcci per líanimazione, alcune tecniche di base risultano particolarmente importanti nel caso delle figure articolate. Consideriamo líesempio del braccio meccanico, e supponiamo di voler muovere la punta del braccio superiore. Il modello ha tre gradi di libertà, che corrispondono ai tre angoli di giunzione. Ad ogni insieme di angoli, si può fare corrispondere uníunica posizione del braccio meccanico, ma il viceversa non è vero. Data una locazione nello spazio, potrebbe non esserci nessun insieme di angoli in grado di posizionare il braccio nella locazione desiderata, oppure potrebbero esserci più scelte per i valori degli angoli in grado di posizionare il braccio in quella locazione.
La descrizione della posizione delle parti del modello sulla base dei soli angoli di giunzione è uno degli argomenti di studio della cinematica. I metodi di modellazione gerarchica possono essere utilizzati per derivare un modello cinematico, cioè le equazioni esplicite che danno la posizione di qualsiasi insieme di punti nel modello in termini degli angoli di giunzione. Così, se q rappresenta il vettore degli angoli di giunzione, e p è il vettore i cui elementi sono i vertici del modello, il modello cinematico sarà composto da uníequazione del tipo p = f(q).
Il modello cinematico trascura alcuni effetti, quali líinerzia e gli attriti. Eí comunque possibile derivare delle equazioni differenziali più complesse, che descrivono il comportamento dinamico dei modelli in termini delle forze applicate.
Il problema cruciale nelle tecniche di animazione,
è un problema di tipo inverso rispetto ai problemi
classici di cinematica e dinamica: dato uno stato del modello
che si desidera raggiungere, come aggiustare gli angoli di giunzione
in modo da raggiungere questa posizione? Ci sono due questioni
immediatamente collegate:
Molto spesso risulta estremamente difficile eseguire questi compiti, e per superare queste difficoltà si può seguire un approccio che deriva dalle tecniche tradizionali di animazione manuale, chiamato key-frame animation. Seconda questa tecnica, gli oggetti sono posizionati nello spazio solo a certi istanti di tempo, creando i cosiddetti quadri-chiave. I quadri rimanenti possono essere automaticamente riempiti interpolando gli angoli di giunzione dei quadri chiave, o, equivalentemente, usando una semplice approssimazione per ottenere le equazioni dinamiche richieste per passare da un quadro chiave allíaltro.
Nella descrizione di una scena intervengono, oltre alle descrizioni delle primitive grafiche e degli oggetti geometrici, anche altri fattori, quali líilluminazione e la posizione dellíosservatore. Anche questi fattori possono essere definiti con vertici e vettori, e possono essere dotati di attributi simili a quelli associati alle primitive geometriche.
 Figura
11.6 Albero di scena.
Figura
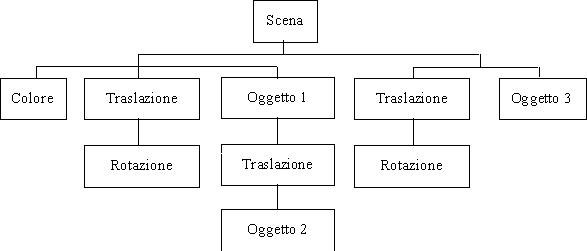
11.6 Albero di scena.La struttura ad albero introdotta per descrivere i modelli gerarchici, può essere estesa in modo da descrivere le relazioni tra gli oggetti geometrici e gli altri fattori. Possiamo cioè estendere la nozione di contenuto di un grafo per poter descrivere líintera scena. Una possibilità è quella di usare una struttura dati ad albero ed includere in ogni nodo, oltre alla matrice model-view ed al puntatore alla funzione di drawing, anche vari attributi. Uníaltra possibilità è consentire líintroduzione di nuovi nodi per la definizione degli attributi e per la specificazione delle matrici di trasformazione. Ad esempio, nellíalbero mostrato nella Figura 11.6sono stati inseriti dei nodi per specificare il colore e le matrici model-view, e alcuni nodi separatori (che non modificano lo stato e non provocano la visualizzazione di nessuna primitiva).
Se visitiamo líalbero da sinistra a destra,
con un algoritmo di depth-first search, il codice OpenGL
corrispondente è della forma seguente:
glPushAttributesglPushMatrixglColorglTranslateglRotateobject1()glTranslateobject2()glPopMatrixglPushMatrixglTranslateglRotateobject3()glPopMatrixglPopAttributes
Líalbero di scena che abbiamo descritto è equivalente ad un programma OpenGL, nel senso che possiamo utilizzare líalbero per generare in modo assolutamente meccanico il codice OpenGL. Questo approccio è seguito da Open Inventor, un programma object-oriented che, dato un programma Inventor, ossia una descrizione di un albero di scena, visita líalbero ed esegue le funzioni grafiche, che sono scritte in OpenGL.
I modelli language-based forniscono un metodo alternativo di rappresentazione delle relazioni gerarchiche tra gli oggetti, ed anche un metodo procedurale di definizione degli oggetti.
Fino ad ora, abbiamo sempre definito gli oggetti geometrici generando le primitive necessarie, sulla base di un modello fissato, indipendentemente dal fatto che tali primitive risultino poi visibili. Un metodo alternativo di definizione degli oggetti geometrici consiste nellíusare algoritmi e procedure per generare le primitive. Questo approccio permette di evitare di generare tutto líoggetto prima dello stadio di rendering, stadio in cui si determina quali primitive sono effettivamente necessarie. I modelli procedurali hanno líulteriore vantaggio di poter essere utilizzati assieme a dispositivi di generazione di numeri casuali, in modo che ogni esecuzione della procedura genera un oggetto geometrico simile agli altri nelle sue proprietà globali, ma differente nei dettagli. Questi metodi sono particolarmente utili per generare immagini di oggetti del mondo reale, come ad esempio piante e terreni.
In informatica, le strutture dati ad albero sono utilizzate per descrivere il parsing delle sentenze, ossia la loro scomposizione nelle parti costitutive, sia nei linguaggi naturali, che in quelli del calcolatore. Nei programmi, líesecuzione del parsing fa parte del processo di compilazione; mentre per i linguaggi naturali, il parsing delle sentenze è eseguito per verificare se la sentenza è grammaticalmente corretta. Líalbero risultante dal parsing di una sentenza corretta, fornisce la struttura, o sintassi, della sentenza. Líinterpretazione degli elementi individuali nellíalbero - le parole - fornisce il significato - la semantica - della sentenza.
Se consideriamo solo la sintassi di un linguaggio, cíè una correlazione diretta tra le regole del linguaggio e la forma dellíalbero che rappresenta la sentenza. Una grammatica è definita da un insieme di simboli e da un insieme di regole, o produzioni, che specificano come sostituire un simbolo con uno o più altri simboli:
A Æ BC,
B Æ ABA.
Dato un insieme di produzioni, possiamo generare un numero infinito di stringhe. In generale, cíè più di una regola che può essere applicata ad un dato simbolo ad ogni istante, e, selezionando in modo casuale la regola da applicare, si può generare una stringa diversa ad ogni esecuzione del programma. Inoltre, è possibile scrivere dei programmi che non solo generano stringhe, ma che, data una stringa in input, sono in grado di stabilire se la stringa appartiene allíinsieme di stringhe generabili dalle produzioni della grammatica. Dal punto di vista grafico, possiamo allora pensare di avere un insieme di regole per generare un certo tipo di oggetto, ed un programma che può identificare gli oggetti in una scena sulla base della grammatica che li ha generati.
Líinterpretazione dei simboli in una stringa converte la stringa in un oggetto grafico. Ci sono diversi modi per generare regole e per interpretare le stringhe risultanti come oggetti grafici. Un approccio possibile è quello adottato nel sistema della ìgrafica della tartarugaî. In questo sistema vi sono tre metodi base per manipolare un cursore grafico, detto anche tartaruga. La tartaruga si può muovere di un passo in avanti, girare a destra, o girare a sinistra. Supponiamo che gli angoli di cui la tartaruga può curvare siano fissati. Utilizziamo la notazione F, R, L per indicare le tre operazioni. Ogni stringa di operazioni ha uníinterpretazione grafica immediata. Ad esempio, se líangolo è di 120_, la stringa FRFRFR genera un triangolo equilatero. Utilizziamo i simboli [ e ] per indicare il pushing e il popping dello stato della tartaruga (la sua posizione e la sua orientazione) in una pila. Consideriamo ora la produzione
F Æ FLFRRFLF,
con un angolo di 60_. Líinterpretazione grafica delle regola è mostrata nella Figura 11.7.
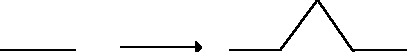 Figura
11.7 Produzione della curva di Koch.
Figura
11.7 Produzione della curva di Koch.Se applichiamo la regola in parallelo a tutte le istanze di F, otteniamo le cosiddette curve di Koch. In particolare, se applichiamo la produzione ad un triangolo, otteniamo una curva chiusa chiamata snowflake (fiocco di neve). Queste curve appartengono alla categoria delle curve space-filling: se applichiamo ricorsivamente la regola di produzione, la curva diventa sempre più lunga senza mai incrociarsi, e continuando ad occupare una regione limitata dello spazio bidimensionale.
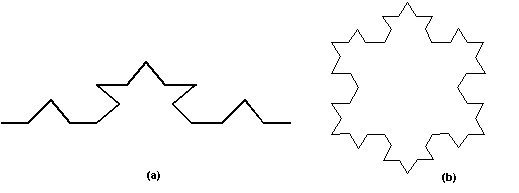 Figura 11.8 Curve
space-filling. (a) curva di Koch; (b) snowflake.
Figura 11.8 Curve
space-filling. (a) curva di Koch; (b) snowflake.Supponiamo di voler creare il modello di una pianta. Le operazioni push e pop permettono di sviluppare i rami. Consideriamo ad esempio la regola
F Æ F [RF ]F [LF ]F,
con un angolo di 27_. Partendo da un semplice segmento lineare, si ottiene il risultato mostrano in Figura 11.9(a). A questo punto possiamo procedere in diversi modi. Possiamo riapplicare la regola ad ogni F nella sequenza ottenuta, e otteniamo líoggetto mostrato nella Figura 11.9 (b).
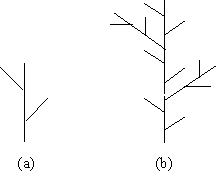 Figura 11.9 (a)
La regola F Æ F
[RF ]F [ LF ]F.
(b) Seconda iterazione della regola.
Figura 11.9 (a)
La regola F Æ F
[RF ]F [ LF ]F.
(b) Seconda iterazione della regola.Possiamo inoltre modificare la lunghezza dello spostamento in avanti della tartaruga, così che i rami diventino sempre più piccoli nelle iterazioni successive. Líoggetto geometrico ottenuto assomiglia ad una pianta, e la somiglianza aumenta con líaumentare delle iterazioni. Tuttavia, disponendo di una singola regola, e applicandola in parallelo, si ottiene sempre lo stesso oggetto. Una strategia più intelligente consiste nellíapplicare la regola casualmente alle occorrenze del simbolo F. In questo modo, si possono ottenere oggetti globalmente simili, ma differenti nei dettagli, con i quali si può modellare una pianta in modo più realistico.
Una delle attrattive di questa strategia è la possibilità di definire una classe di oggetti sulla base di poche regole e di pochi parametri. Supponiamo di voler creare un gruppo di piante. Líapproccio diretto consiste nel generare tanti oggetti quanti sono ritenuti necessari e nel rappresentarne ciascuno come una collezione di oggetti geometrici (linee, poligoni, curve). A seconda delle condizioni di viewing, la maggior parte di queste primitive potrebbe poi non apparire nellíimmagine, perché esclusa in fase di clipping, oppure perché troppo lontana dallíosservatore per poter essere visualizzata ad una dimensione visibile. Invece, applicando il metodo procedurale descritto, possiamo descrivere gli oggetti tramite algoritmi semplici e generare gli oggetti geometrici solo quando necessario.
Possiamo descrivere una grammatica anche direttamente in termini di forme e trasformazioni affini, creando una ìgrammatica delle formeî. Ad esempio, nella generazione dello Sierpinsky gasket, possiamo definire il passo di suddivisione in termini di tre trasformazioni affini, ciascuna delle quali esegue una scalatura del triangolo originale, e piazza la copia più piccola in una posizione differente.
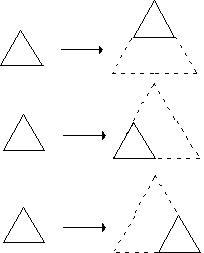 Figura 11.10 Le
tre regole per generare lo Sierpinsky gasket.
Figura 11.10 Le
tre regole per generare lo Sierpinsky gasket.Possiamo applicare le tre regole parallelamente, oppure casualmente, e al limite, il risultato ottenuto in entrambi i casi è esattamente lo Sierpinsky gasket.
Si osservi che gli esempi delle curve di Koch e dello Sierpinsky gasket sono entrambi basati su un metodo che può essere applicato ricorsivamente e che, quando è eseguito, genera dettagli che nella forma riproducono líoggetto di partenza. Si tratta dello stesso metodo che è alla base della geometria dei frattali, applicata in computer graphics non solo per ottenere oggetti complessi, ma anche per modellare entità del mondo reale, non facilmente modellabili con altri metodi.
In computer graphics, gli oggetti di cui si creano le immagini potrebbero non avere alcuna connessione con la realtà fisica. Questa flessibilità, da un lato permette di visualizzare forme che non esistono nello spazio tridimensionale, e costruire modelli di oggetti che non sono limitati dalle proprietà dei materiali di cui sono costituiti, ma dallíaltro può rendere impossibile simulare correttamente gli oggetti del mondo reale. Ad esempio, mentre è facile costruire il modello di un gruppo di oggetti in movimento nello spazio, è molto più difficile tenere traccia delle possibili collisioni tra gli oggetti, e creare un sistema grafico che si comporti in un modo fisicamente corretto.
I modelli basati sulla fisica sono modelli
in cui gli oggetti grafici obbediscono alle leggi fisiche. Questa
tecnica di modellazione può seguire uno tra i seguenti
approcci:
I sistemi a particelle sono basati sul secondo approccio. Questi sistemi sono composti da collezioni di particelle, il cui comportamento dinamico può essere determinato risolvendo un insieme di equazioni differenziali. I sistemi a particelle possono essere utilizzati per generare e simulare uníampia varietà di comportamenti: in fluidodinamica sono utilizzati per modellare le turbolenze, e in computer graphics per modellare diversi fenomeni, quali fuochi díartificio, azioni ondulatorie, etc.
Nei sistemi a particelle, ogni particella può essere trattata come una massa puntiforme. Líapplicazione delle leggi fisiche permette di scrivere le equazioni differenziali che descrivono lo stato delle particelle ad ogni istante di tempo. Risolvendo numericamente queste equazioni, possiamo visualizzare ogni particella come un oggetto grafico.
Consideriamo un insieme di particelle soggette alle leggi di Newton. Ogni particella deve obbedire alla seconda legge di Newton, che stabilisce che la massa (m) della particella, moltiplicata per líaccelerazione (a) è uguale alla forza risultante (f ) che agisce sulla particella:
f = ma.
Se la particella i è puntiforme, il suo stato ad ogni istante di tempo è definito da due vettori tridimensionali: il vettore posizione
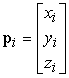
e il vettore velocità
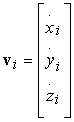
Dato che líaccelerazione è la derivata della velocità, e la velocità è la derivata della posizione, possiamo scrivere la seconda legge di Newton relativa allíi-esima particella sotto forma di sei equazioni differenziali accoppiate:
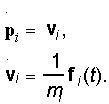
Quindi, la dinamica di un sistema di n particelle è governata da 6n equazioni differenziali accoppiate.
Oltre allo stato, ad ogni particella può essere associato un certo insieme di attributi, che comprendono la massa (mi) e altre proprietà che governano il suo comportamento e la sua visualizzazione (forma, colore, proprietà superficiali, etc.). Si osservi che, sebbene le particelle siano considerate come masse puntiformi dal punto di vista dinamico, líutente può comunque specificare il modo in cui la particella dovrà essere visualizzata: una particella può rappresentare una persona in una scena affollata, oppure una molecola nella simulazione di un processo chimico. In ogni caso, il sistema descrive locazione, velocità e centro di massa delle particelle, e quando la locazione di una particella è nota, vi possiamo piazzare líoggetto desiderato.
Il comportamento di un sistema di particelle è
governato da un insieme di forze {fi},
variabile nel tempo. Queste forze sono basate sui principi e sui
vincoli fisici imposti sul sistema. Se pensiamo al sistema di
n particelle come ad un sistema con 6n variabili,
un passo temporale tipico è basato sulla computazione delle
forze che si applicano in quel particolare istante, attraverso
una funzione definita dallíutente, e queste forze vengono
usate per aggiornare lo stato. In codice, abbiamo un ciclo della
forma
float time, delta;float
state[6n]. force[3n]state=get_initial_state();for(time=t0; time<time_final;
time+=delta){force=force_function(state, time);state=ode(force,
delta); /* standard differential equation solver */}
La componente principale che deve essere progettata è la funzione che calcola le forze che agiscono su ogni particella. Ci sono diversi modi per descrivere queste forze. Se le forze che agiscono su una particella sono indipendenti dalle altre particelle, allora la forza che agisce sullíi-esima particella può essere descritta dallíequazione
fi = fj (pi,, vj).
Un caso semplice è quello in cui le particelle sono soggette solo alla forza gravitazionale:
fi = g,
dove g può essere rappresentata dal vettore
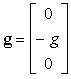
Sotto líazione di questa forza, ogni particella si muove lungo una traiettoria parabolica. Se gli attributi variano nel tempo, e ad ogni particella viene assegnato un tempo di vita casuale, possiamo simulare graficamente fenomeni come i fuochi díartificio. Più in generale, se permettiamo alla particella di muoversi casualmente, e visualizziamo ciascuna particella sotto forma di un oggetto di dimensioni notevoli, piuttosto che un singolo punto, possiamo modellare nuvole o flussi di particelle indipendenti.
Se in un sistema di n particelle, tutte le particelle sono indipendenti, il calcolo delle forze ha una complessità di ordine O(n). Nella maggioranza dei casi, tuttavia, nella computazione delle forze che agiscono su una singola particella, occorre considerare anche le interazioni della particella con le altre particelle del sistema, e la complessità risulta di ordine O(n2). Questo ordine di complessità può essere ridotto se si introduce líipotesi che una particella interagisca solo con le particelle vicine.
Uno dei possibili metodi per modellare le forze di interazione tra le particelle, consiste nel considerare le particelle adiacenti connesse da una molla. In questo caso, líinterazione è governata dalle forze elastiche, che obbediscono alla legge di Hook:
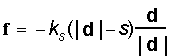
dove 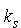
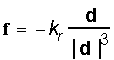
e sono dunque inversamente proporzionali al quadrato della distanza tra le particelle.
Per quanto riguarda infine i vincoli fisici che agiscono sui sistemi di particelle, questi possono essere divisi in due classi: i vincoli hard e i vincoli soft.
I vincoli hard sono quelli che devono essere aderenti alla realtà. Ad esempio una palla che colpisce un muro deve rimbalzare, e non attraversarlo. Inoltre, non possiamo nemmeno permettere che la palla si avvicini semplicemente al muro e poi rimbalzi, perché è necessario che essa colpisca effettivamente il muro.
La gestione dei vincoli soft è più
semplice. Supponiamo di volere che una particella, posizionata
nel punto p, rimanga sempre nei pressi di un punto p0.
A questo scopo, possiamo introdurre una funzione penalità
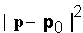
La visualizzazione scientifica è un campo di studio il cui obiettivo è quello di visualizzare grosse quantità di dati multidimensionali, sfruttando le capacità hardware e software dei sistemi grafici. Quando si lavora con grossi insiemi di dati non è affatto chiaro come questi dati debbano essere rappresentati graficamente. I numeri che vogliamo visualizzare non hanno infatti una rappresentazione visuale. Inoltre, le tecniche di base per tracciare i grafici (plotting) ñ quali istogrammi, diagrammi a torta, etc. ñ sono adatte ad insiemi monodimensionali di dati. Insiemi di dati in due o tre dimensioni richiedono invece metodi di visualizzazione più sofisticati.
La visualizzazione scientifica fornisce varie possibilità per effettuare la conversione dei dati in oggetti geometrici, consentendone la visualizzazione. Esamineremo nel seguito due metodi particolari: i contour plot per i dati bidimensionali e il metodo delle isosuperfici per i dati tridimensionali.
Supponiamo di avere un insieme di dati bidimensionali
{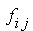
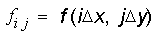
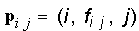
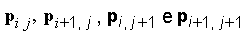
Queste tecniche sono ampiamente applicate, ma hanno la limitazione di non estendersi bene agli insiemi di dati tridimensionali (o volumetrici) { fi j k }. Al contrario, la tecnica del contour plotting può essere estesa facilmente anche al caso tridimensionale.
Consideriamo líequazione
f (x, y) = c,
dove c è una costante. Le coppie x, y che soddisfano questa equazione definiscono il contorno della funzione. Se f è una funzione che si comporta ragionevolmente bene, i contorni corrispondono a curve chiuse, del tutto simili alle curve che si usano sulle carte topografiche per rappresentare líaltitudine delle zone montuose. Vediamo allora come applicare questa tecnica nel caso di dati bidimensionali. Difficilmente un campione di dati { fi j}, contiene molti valori che soddisfano líequazione
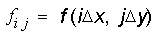
Tuttavia, se consideriamo i dati ai vertici della cella definita dai quattro punti adiacenti (i, j), (i+1, j), (i, j+1) e (i+1, j+1), è possibile ottenere una buona stima del comportamento locale di una curva di contorno.
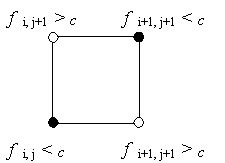 Figura
11.11 Cella con vertici colorati in base
al valore associato.
Figura
11.11 Cella con vertici colorati in base
al valore associato. Consideriamo la cella mostrata nella Figura 11.11, dove i vertici sono stati colorati di bianco o nero a seconda che il valore associato sia maggiore (bianco) o minore (nero) del valore scelto per il contorno, c. Scegliendo sempre la spiegazione più semplice per interpretare la colorazione dei vertici, si può inferire líandamento della curva di contorno dal colore dei vertici. Ad esempio, se i quattro vertici hanno lo stesso colore, líinterpretazione più semplice è che il contorno non passa attraverso la cella. Se una cella ha un vertice bianco e tre neri, possiamo invece supporre che il contorno taglia la cella attraverso i due lati che condividono il vertice bianco. Possiamo quindi usare i valori di fi j nei vertici per interpolare le locazioni approssimate in cui il contorno interseca i lati della cella.
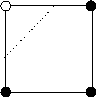 Figura 11.12 Interpretazione
di una cella.
Figura 11.12 Interpretazione
di una cella.
Connettendo i punti di intersezione con un segmento
lineare, si costruisce progressivamente una spezzata che costituisce
uníapprossimazione di primo grado per la curva di contorno.
Nonostante ci siano 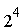
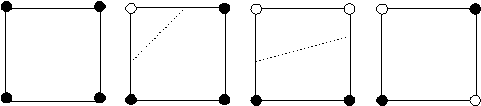 Figura 11.13 Colorazioni
delle celle.
Figura 11.13 Colorazioni
delle celle. Nei primi tre casi, è facile individuare il contributo della cella alla curva di contorno. Il quarto caso risulta invece ambiguo, poiché può essere interpretato in due modi differenti.
In mancanza di informazioni addizionali, non è possibile risolvere questa ambiguità scegliendo una delle due interpretazioni. In questi casi si può decidere di risolvere la situazione scegliendo a caso una delle due interpretazioni, oppure considerando la situazione delle celle adiacenti prima di fare la scelta. Un terzo approccio consiste nel dividere la cella in quattro parti, e interpolare un valore centrale da utilizzare per risolvere, se possibile, líambiguità.
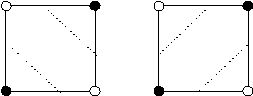 Figura 11.14 Celle
ambigue.
Figura 11.14 Celle
ambigue. Uno dei principali vantaggi della tecnica basata sulle linee di contorno sta nel fatto che le singole celle sono elaborate indipendentemente, e quindi questa tecnica risulta facilmente parallelizzabile.
Supponiamo ora di voler visualizzare un insieme volumetrico di dati {fi j k}. Possiamo interpretare ogni valore fi j k come una campionatura di una funzione f (x, y, z) sui punti di una griglia tridimensionale.
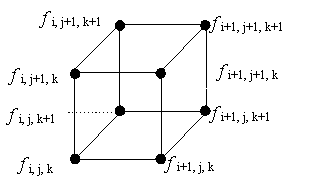 Figura 11.15 Cella
di dati volumetrici.
Figura 11.15 Cella
di dati volumetrici. La tecnica delle isosuperfici è una tecnica di visualizzazione dei dati volumetrici che crea degli oggetti geometrici a partire da sottoinsiemi di dati, e quindi usa il sistema grafico per visualizzare questi oggetti. Le isosuperfici sono le soluzione dellíequazione
f (x, y, z) = c.
Fissato un valore di c, potrebbero non esserci soluzioni, oppure potrebbero esserci più soluzioni. Se consideriamo líinsieme di dati { fi j k } come una campionatura di una funzione f (x, y, z), possiamo usare questi dati per costruire le approssimazioni delle isosuperfici sotto forma di mesh di poligoni. Supponendo di essere in grado di visualizzare in modo accurato i triangoli tridimensionali, si può applicare un metodo, chiamato metodo dei marching cubes, per approssimare le superfici tramite mesh di triangoli.
Per ogni cella della griglia tridimensionale, si determina la parte di isosuperficie che la attraversa sulla base dei valori della funzione nei vertici della cella. Dato un valore per la costante c che definisce una isosuperficie, coloriamo i vertici della cella di nero o di bianco, a seconda che il valore associato sia maggiore o minore della costante c. In questo caso ci sono 28 colorazioni possibili, che possono essere ridotte a 14 tenendo conto delle simmetrie.
 Figura 11.16 Colorazioni
dei vertici.
Figura 11.16 Colorazioni
dei vertici. Scegliendo ogni volta líinterpretazione dei dati più semplice, possiamo generare i punti di intersezione tra la superficie i lati dei cubi effettuando uníinterpolazione lineare dei valori dei vertici. Infine, possiamo usare dei triangoli per tassellare le intersezioni, generando in questo modo una parte di un mesh di triangoli che approssima la isosuperficie.
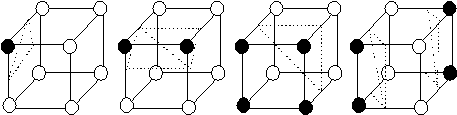 Figura 11.17 Alcuni
esempi di tassellazione delle celle.
Figura 11.17 Alcuni
esempi di tassellazione delle celle. Ogni cella può essere elaborata indipendentemente, e quindi líalgoritmo che implementa questa tecnica può essere facilmente parallelizzato. Come nel caso delle curve di contorno, anche per le isosuperfici possono verificarsi delle situazioni di ambiguità. In particolare, líambiguità sorge tutte le volte che ci sono colori diversi assegnati a vertici diagonalmente opposti di una faccia della cella.
 Figura 11.18 Un
caso di ambiguità.
Figura 11.18 Un
caso di ambiguità. Purtroppo non esiste un approccio per risolvere sempre tutte le situazioni di ambiguità, e per avere soluzioni sempre corrette in alcuni casi è indispensabile disporre di informazioni addizionali.
La tecnica che abbiamo descritto può essere considerata sia come una tecnica di riduzione di dati, che come una tecnica di modellazione. Molto spesso, gli insiemi di dati generati nelle simulazioni possono avere cardinalità di ordine compreso tra 107 e 109. Con insiemi così vasti, il costo computazionale in tempo e spazio di memoria anche di operazioni semplici (come scalature e rotazioni dellíinsieme di dati) può diventare molto pesante. In molte applicazioni, tuttavia, dopo aver eseguito líalgoritmo marching cubes, i dati possono essere ridotti a O(104) triangoli tridimensionali, un numero di oggetti geometrici che può essere facilmente elaborato da un sistema grafico. Ciò consente di ruotare, colorare e ombreggiare le superfici in tempi più che ragionevoli, e permettendo allíutente di interpretare i dati in tempo reale.