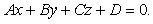 (10.1)
(10.1)
Un mesh di poligoni è costituito da una collezione di lati, vertici e poligoni connessi tra loro in modo tale che ciascun lato è condiviso da al più due poligoni. Un lato connette due vertici, e un poligono è una sequenza chiusa di lati. Un lato può essere condiviso da due poligoni adiacenti, un vertice è condiviso da almeno due lati, e ogni lato deve infine essere parte di qualche poligono.
Un mesh di poligoni può essere rappresentato in diversi modi, inoltre si può ricorrere a rappresentazioni diverse anche allíinterno di una singola applicazione. Infatti, si può scegliere una rappresentazione per la memorizzazione esterna, una per uso interno, e uníaltra ancora per creare il mesh in modo interattivo.
I criteri di base per valutare le diverse rappresentazioni sono il costo in tempo e in spazio delle rappresentazioni stesse. Le operazioni tipiche su un mesh di poligoni sono: trovare tutti i lati incidenti ad un certo vertice; individuare i vertici connessi da un lato; trovare i lati di un poligono; visualizzare il mesh; identificare eventuali errori nella rappresentazione (ad esempio vertici, o lati, o poligoni mancanti).
Discuteremo tre tipi di rappresentazione: la rappresentazione esplicita, la rappresentazione con puntatori ad una lista di vertici, e la rappresentazione con puntatori ad una lista di lati.
Nella rappresentazione esplicita, ogni poligono è rappresentato da una lista di coordinate di vertici: P = ((x1, y1, z1), (x2, y2, z2), Ö , (xn, yn, zn)). I vertici sono memorizzati nellíordine secondo il quale vorremmo incontrarli viaggiando lungo il poligono. In altre parole, le coppie di vertici successivi sono connesse da lati, inoltre cíè un lato che connette líultimo vertice della lista al primo. Per un poligono singolo, questa rappresentazione è efficiente in spazio; per un mesh di poligoni, invece, viene usato inutilmente dello spazio poiché le coordinate dei vertici condivisi sono memorizzate due volte. Inoltre manca una rappresentazione esplicita dei lati e dei vertici condivisi. Ad esempio per trascinare un vertice assieme a tutti i lati ad esso incidenti, in una tipica applicazione interattiva, dobbiamo trovare tutti i poligoni che condividono il vertice selezionato. Questa ricerca richiede diversi confronti tra le coordinate dei vertici di un poligono con quelle di tutti gli altri poligoni. Il metodo più efficiente per eseguire questo compito sarebbe quello di ordinare tutte le N coordinate, operazione che richiede nel migliore dei casi un tempo dellíordine di N log2 N. Inoltre esiste anche la possibilità che, a causa degli arrotondamenti dovuti alla computazione, uno stesso vertice possa trovarsi ad avere coordinate diverse in ogni poligono. Per quanto riguarda la visualizzazione, questa rappresentazione richiede la trasformazione di ogni vertice e il clipping di ogni lato di ciascun poligono. Inoltre, i lati condivisi vengono disegnati due volte, e questo può introdurre degli inconvenienti dovuti alla sovrascrittura.
Nei poligoni definiti usando i puntatori a liste di vertici, ogni vertice del mesh di poligoni è memorizzato nella lista di vertici V = ((x1, y1, z1), (x2, y2, z2), Ö , (xn, yn, zn))), una sola volta. Un poligono è quindi definito da una lista di puntatori alla lista di vertici. Questa rappresentazione presenta diversi vantaggi. Per prima cosa garantisce un notevole risparmio di spazio di memoria. Inoltre, le coordinate di un vertice possono essere modificate facilmente. Díaltro canto, tuttavia, risulta ancora computazionalmente difficile trovare i poligoni che condividono un lato, e i lati condivisi sono di nuovo disegnati due volte.
Possiamo eliminare questi due problemi rappresentando i lati in modo esplicito, come avviene nella rappresentazione tramite puntatori a liste di lati. In questo caso, abbiamo ancora una lista V di vertici, ma il poligono è rappresentato da una lista di puntatori ad una lista di lati, in cui ciascun lato appare una sola volta. Inoltre, in corrispondenza di ciascun lato nella lista, vi sono due puntatori alla coppia di vertici, memorizzati nella lista di vertici, che ne definiscono gli estremi, e uno o due puntatori ai poligoni cui il lato appartiene. Dunque, un poligono è descritto dalla lista P = (L1, L2, Ö , Ln) e un lato dalla lista E = (V1, V2, P1, P2). Quando un lato appartiene ad un solo poligono, P1, oppure P2, sarà nullo. I poligoni vengono rappresentati sul display visualizzandone i lati, in modo da evitare operazioni ridondanti di clipping e scan conversion.
In nessuna delle tre rappresentazioni, la determinazione dei lati incidenti ad un certo vertice può essere fatta in modo efficiente: tutti i lati devono essere ispezionati. Naturalmente, è possibile aggiungere delle informazioni esplicite per permettere di determinare in modo più efficiente queste relazioni.
Quando si lavora con i poligoni, o con mesh di poligoni, spesso è necessario conoscere líequazione del piano su cui giace il poligono. In alcuni casi, líequazione è nota implicitamente dal metodo di costruzione interattiva usato per definire il poligono. Se líequazione non è nota, possiamo usare le coordinate di tre vertici per individuare il piano. Líequazione del piano è definita da
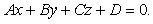
I coefficienti A, B e C definiscono
la normale al piano, cioè il vettore 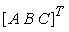
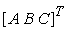
Se ci sono più di tre vertici, essi potrebbero non essere planari, sia per ragioni numeriche, sia a causa del metodo utilizzato per la generazione dei poligoni. In questo caso è opportuno utilizzare uníaltra tecnica per determinare líequazione del piano che più si avvicina ai vertici. Si può dimostrare che A, B e C sono proporzionali alle aree (cui è assegnato un segno) delle proiezioni dei poligoni sui piani (y, z), (z, x), e (x, y), rispettivamente. Ad esempio, se il poligono è parallelo al piano (x, y), risulterà A = B = 0, poiché le proiezioni del poligono sui piani (y, z) e (z, x) hanno area nulla.
Una volta che líequazione del piano è stata determinata, possiamo verificare di quanto il poligono risulti non planare calcolando la distanza ortogonale del piano da ogni vertice. La distanza d relativa al vertice in posizione (x, y, z) è data da
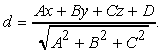
Questa distanza può essere positiva o negativa a seconda di dove è posizionato il punto rispetto al piano (sopra o sotto, a destra o a sinistra). Il segno di d determina infatti da quale parte si trova il punto, e se questa è la sola informazione che ci interessa, la divisione per la radice quadrata non è più necessaria.
Líequazione del piano non è unica; infatti ogni costante moltiplicativa k, diversa da zero, cambia líequazione ma non il piano. Spesso risulta conveniente normalizzare i coefficienti del piano, dividendoli per la costante di normalizzazione
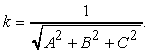
Ciò consente di calcolare più agevolmente la distanza di un punto dal piano, poiché il denominatore dellíequazione (10.2) risulta uguale a 1.
Le spezzate poligonali e i poligoni rappresentano una approssimazione di primo grado per le curve e le superfici, rispettivamente. Per raggiungere una accuratezza ragionevole, è necessario creare e memorizzare un gran numero di coordinate di estremi; inoltre la manipolazione interattiva dei dati può risultare complessa poiché è necessario posizionare in modo preciso tutti questi punti. Usando funzioni di grado maggiore è possibile sviluppare un metodo di rappresentazione delle curve più compatto e più facile da manipolare in modo interattivo. Tale metodo, inoltre, consente di ottenere forme più lisce e continue.
Le approssimazioni di grado alto sono basate, a loro volta, su tre metodi. Nel primo metodo, y e z sono espresse come funzioni esplicite di x: y = f(x) e z = g(x). Le difficoltà dovute a questo approccio sono: (1) líimpossibilità di ottenere valori multipli di y in corrispondenza di un singolo valore di x, quindi le curve quali cerchi e ellissi devono essere rappresentate tramite segmenti multipli di curve; (2) questa definizione non è invariante per rotazioni; e (3) descrivere le curve con le tangenti verticali è difficile, poiché è difficile rappresentare una pendenza infinita.
Nel secondo metodo le curve sono modellate dalle soluzioni di equazioni implicite della forma f(x, y, z) = 0. Anche questo metodo, tuttavia, può presentare alcuni inconvenienti. Líequazione potrebbe avere più soluzione di quante se ne desiderino. Ad esempio, per modellare una circonferenza potremmo usare líequazione x2 + y2 = 1. Ma per modellare solo metà della circonferenza siamo costretti ad aggiungere un vincolo, come x 0, che non può essere contenuto nellíequazione implicita. Inoltre, se due curve definite implicitamente si incontrano in un punto, potrebbe risultare difficile determinare se le loro direzioni tangenziali concordano nel punto di incontro.
Queste due formulazioni matematiche hanno comunque il vantaggio di permettere di determinare rapidamente se un punto giace sulla curva, oppure da quale parte si trova rispetto alla curva.
La rappresentazione parametrica delle curve, x = x(t), y = y(t), z = z(t), consente di superare tutti i problemi delle rappresentazioni in forma esplicita e implicita. Le curve parametriche sostituiscono líuso della pendenza geometrica, che potrebbe essere infinita, con i vettori parametrici tangenziali, che, come vedremo, non sono mai infiniti. Una curva è approssimata da una curva polinomiale a tratti, anziché da una curva lineare a tratti. Ogni segmento Q della curva globale è dato da tre funzioni, x, y, e z, che sono polinomi di terzo grado nel parametro t. Le cubiche sono usate molto spesso poiché i polinomi di grado inferiore consentono poca flessibilità nel controllare la forma della curva, mentre quelli di grado superiore richiedono una computazione più pesante. Nessuna rappresentazione di grado inferiore al terzo consente di interpolare con una curva due estremi specificati, con derivate specificate ad ogni estremo. Data una cubica, e quattro condizioni iniziali, è possibile determinare i suoi quattro coefficienti. Le condizioni iniziali sono date dai due estremi e dalle derivate nei due estremi. Analogamente, i due coefficienti di una retta sono determinati dai due estremi; mentre le derivate negli estremi sono determinate dalla linea stessa e non possono essere controllate indipendentemente. I polinomi di secondo grado, dotati di tre coefficienti, sono determinati dai due estremi più una terza condizione, ad esempio la pendenza o un terzo punto.
I polinomi di terzo grado che definiscono il segmento curvilineo
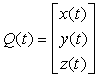
sono della forma
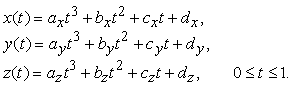
Per visualizzare una curva parametrica si deve valutare líequazione (10.4) per n valori successivi di t, separati da un passo di dimensione Per trattare con segmenti curvilinei finiti si limita il parametro t, senza perdere di generalità, allíintervallo [0, 1].
Introducendo il vettore
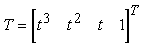
e la matrice C dei coefficienti
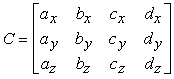
possiamo riscrivere líequazione (10.4) in forma più compatta:
Q(t) = C _ T. (10.6)
La derivata di Q(t) definisce il vettore tangente parametrico della curva. Applicando questa definizione allíequazione (10.6), abbiamo
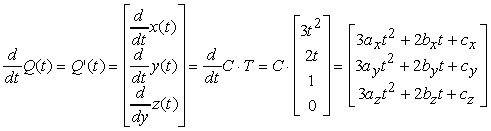
Se due segmenti curvilinei si congiungono, si dice che la curva ha continuità geometrica G0. Se le direzioni (e non necessariamente i moduli) dei due vettori tangenti ai segmenti curvilinei coincidono nel punto di giunzione, si dice che la curva ha continuità geometrica di tipo G1. Questo tipo di continuità, richiesta da molte applicazioni della computer graphics, discende dal fatto che le pendenze geometriche dei segmenti curvilinei sono uguali nel punto di giunzione.
Se i vettori tangenti di due segmenti curvilinei cubici sono uguali sia in modulo che in direzione nel punto di giunzione, la curva ha una continuità di primo grado nel parametro t, ovvero ha una continuità parametrica, e si dice di classe C1. Se la direzione e il modulo delle derivate n-esime dei segmenti curvilinei nel punto di giunzione sono uguali, la curva è detta di classe Cn. In generale, la continuità di classe C1 implica la continuità geometrica di tipo G1, ma il viceversa non è sempre vero. (Si osservi che un segmento curvilineo parametrico è continuo ovunque, e che la continuità di cui ci stiamo ora occupando è relativa esclusivamente ai punti di giunzione.)
In genere perchÈ due curve si congiungano perfettamente Ë sufficiente che coincidano le direzioni delle loro tangenti coincidano nel punto di giunzione, senza che necessariamente coincidano anche in grandezza: questa Ë la base della continuit‡ geometrica.
Un segmento curvilineo Q(t) è definito dai vincoli posti sugli estremi, sui vettori tangenti, e sulla continuità tra i segmenti curvilinei. Ogni cubica ha quattro coefficienti; dunque sono necessarie quattro costanti per poter derivare un sistema di quattro equazioni in quattro incognite la cui soluzione ci fornisce i quattro coefficienti incogniti. A seconda della scelta delle quattro costanti che definiscono le condizioni iniziali, si distinguono diversi tipi di curve. Le curve di Hermite sono definite tramite i due estremi e i vettori tangenti nei due estremi. Le curve di Bézier sono definite dai due estremi e da altri due punti che controllano i vettori tangenti negli estremi. Ci sono poi diversi tipi di curve spline, definite da quattro punti di controllo.
Per comprendere come i coefficienti dellíequazione (10.4) dipendono da quattro vincoli, riscriviamo la matrice dei coefficienti C come prodotto C = G M, dove M è una matrice 4 4 detta matrice base, e G è la matrice geometrica che contiene i quattro vincoli geometrici, cioè le condizioni iniziali che definiscono la curva. Utilizziamo la notazione Gx per indicare il vettore riga composto dalle sole componenti x della matrice geometrica. Gy e Gz sono definite in modo analogo. La matrice geometrica e/o la matrice base sono diverse per ogni tipo di curva.
Gli elementi di G e di M sono costanti, così il prodotto Q(t) = G M T risulta pari a
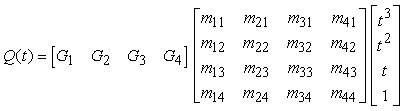
La componente 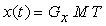
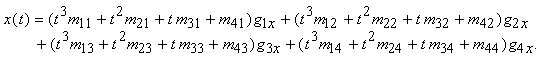
La curva risulta dunque esprimibile tramite una somma pesata degli elementi della matrice geometrica. I pesi sono espressi da polinomi di terzo grado in t, definiti dal prodotto M T, e sono chiamati funzioni blending. Si noti la somiglianza con le approssimazioni di secondo grado a tratti, in cui sono necessari solo due vincoli geometrici (gli estremi), e ogni tratto è dato da un segmento lineare:
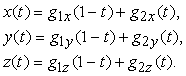
Le curve parametriche cubiche sono dunque una generalizzazione dellíapprossimazione lineare a tratti.
Le curve di Hermite sono determinate dai vincoli sugli estremi, P1 e P4, e dai vettori tangenti negli estremi, R1 e R4. Per trovare la matrice base di Hermite MH che lega la matrice geometrica di Hermite GH ai coefficienti dei polinomi di terzo grado, dobbiamo formare e risolvere il sistema di quattro equazioni, una per ogni vincolo, nei quattro coefficienti polinomiali incogniti. Se definiamo la componente x della matrice geometrica di Hermite, MHx, nel modo seguente
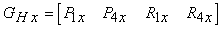
e riscriviamo x(t), definito nelle equazioni (10.4) e (10.9), come
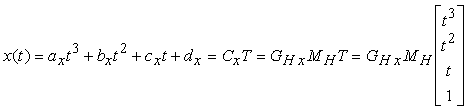
i vincoli su x(0), che deve coincidere con P1, e x(1) che deve coincidere con P4, si trovano per sostituzione diretta nellíequazione (10.12):
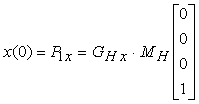
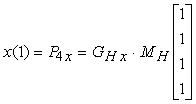
Derivando líequazione (10.12), otteniamo 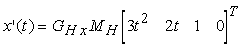
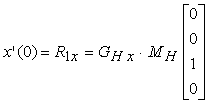
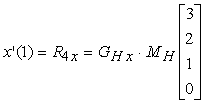
In forma matriciale, risulta
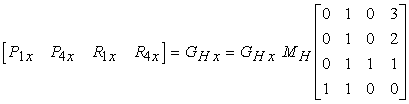
Affinché questa equazione matriciale sia soddisfatta, insieme alle equazioni analoghe relative alle coordinate y e z, MH deve essere uguale alla matrice inversa della matrice presente nellíequazione (10.17):
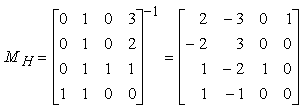
La matrice MH può ora essere utilizzata nellíequazione x(t) = GHx MH T per trovare x(t), e, analogamente, nelle equazioni y(t) = GHy MH T e z(t) = GHz MH T per determinare y(t) e z(t). Possiamo dunque scrivere
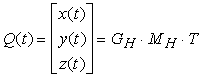
dove MH è la matrice [P1 P4 R1 R4].
Sviluppando il prodotto MH T nellíequazione che definisce Q(t), si ricava la funzione blending di Hermite BH, definita dal polinomio che costituisce il peso di ogni elemento della matrice geometrica:
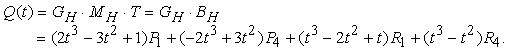
La figura seguente descrive le funziooni di blending di hermite.
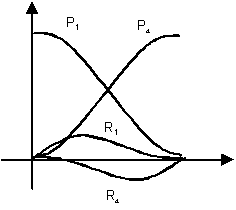 Figura 0.1 Le funzioni
di blending di Hermite.
Figura 0.1 Le funzioni
di blending di Hermite.
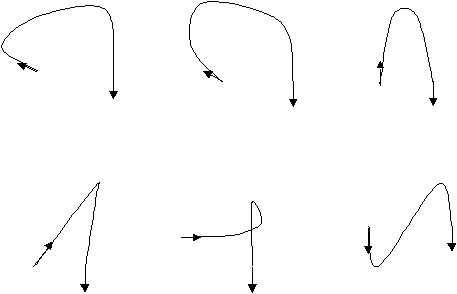 Figura 0.2 Esempi
di curve parametriche di Hermite.
Figura 0.2 Esempi
di curve parametriche di Hermite.Le curve di Bézier sono definite dai due estremi e da altri due punti di controllo intermedi, che non appartengono alla curva, e che specificano in modo indiretto i vettori tangenti negli estremi.
Indichiamo con P1 e P4 gli estremi, e con P2 e P3 i punti intermedi. I vettori tangenti negli estremi, R1 e R2, sono legati ai quattro punti di controllo dalle relazioni:

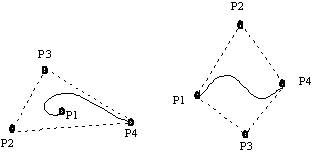 Figura 0.3 Due
curve di Bézier con i relativi punti di controllo.
Figura 0.3 Due
curve di Bézier con i relativi punti di controllo.
La matrice geometrica di Bézier 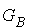
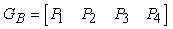
Quindi, la matrice MHB che definisce la relazione GH = GB MHB tra la matrice geometrica di Hermite GH e la matrice geometrica di Bézier GB si ricava riscrivendo líequazione (10.22) in forma matriciale:
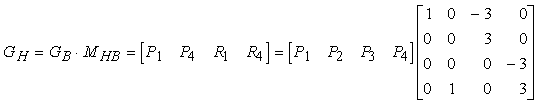
Per trovare la matrice base di Bézier MB, si sostituisce nellíequazione (10.19) GH = GB MHB, e si definisce MB = MHB MH:
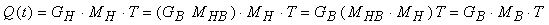
Eseguendo il prodotto MB = MHB MH, si ottiene
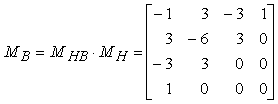
Infine, il prodotto Q(t) = GB MB T risulta pari a
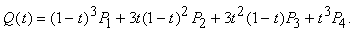
I quattro polinomi BB = MB T, che costituiscono i pesi nellíequazione (10.26), sono chiamati polinomi di Bernstein. Si osservi che la somma di questi quattro polinomi risulta sempre pari ad 1. Inoltre, ciascun polinomio risulta sempre maggiore o uguale a zero, per 0 t < 1. Dunque, Q(t) coincide con la media pesata dei quattro punti di controllo. Questa condizione significa che ogni segmento curvilineo, dato dalla somma dei quattro punti di controllo, pesata dai polinomi di Bernstein, è completamente contenuto nel convex hull dei quattro punti. Il convex hull per le curve sul piano è definito dal poligono convesso formato dai quattro punti di controllo (si veda la figura 10.1). Nel caso tridimensionale, il convex hull è definito dal poliedro convesso formato dai quattro punti.
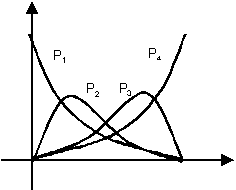 Figura 0.4 I polinomi
di Bernstein.
Figura 0.4 I polinomi
di Bernstein.Questa proprietà vale per tutte le cubiche definite dalla somma pesata dei punti di controllo, quando le funzioni blending sono maggiori o uguali a zero. Inoltre, il fatto che la somma dei polinomi sia sempre uguale a 1 consente di ridurre il tempo computazionale, lavorando con tre soli polinomi e determinando il quarto, per ogni valore di t, per sottrazione.
Infine, questa proprietà può essere sfruttata anche per il clipping: si può applicare un algoritmo di clipping di poligoni, ad esempio líalgoritmo di Sutherland-Hodgman, per effettuare il clipping del convex hull. Se il convex hull è completamente allíinterno del rettangolo di clipping, così è anche per la curva; se il convex hull è completamente allíesterno, lo stesso accade per la curva; quindi solo nei casi intermedi in cui il convex hull interseca i bordi del rettangolo di clipping, è necessario esaminare direttamente il segmento curvilineo.
Una spline cubica naturale è una curva polinomiale cubica, con una continuità di classe C0, C1 e C2, che interpola i punti di controllo. Questo tipo di curva ha un grado di continuità in più rispetto alle curve di Hermite e di Bézier, e quindi risulta di forma più liscia.
I coefficienti polinomiali delle spline naturali dipendono da tutti gli n punti di controllo; quindi per determinarli si rende necessario invertire una matrice n+1 n+1. Ciò introduce due svantaggi: (1) il movimento di un solo punto di controllo influenza tutta la curva, e (2) il tempo computazionale richiesto per líinversione della matrice può causare problemi nelle applicazioni interattive, dove si desidera poter modificare rapidamente la forma di una curva.
Le B-spline sono segmenti curvilinei i cui coefficienti polinomiali dipendono solo da pochi punti di controllo. Dunque, il tempo necessario per determinare i coefficienti risulta fortemente ridotto. Inoltre il movimento di un punto di controllo influenza solo una piccola parte della curva. Questo comportamento è chiamato controllo locale. La ìBî sta per base, infatti le B-spline possono essere rappresentate come somme pesate di funzioni polinomiali di base, a differenza delle spline naturali per cui questa proprietà non è verificata.
Le B-spline hanno lo stesso tipo di continuità delle spline naturali, ma non interpolano i propri punti di controllo. Per descrivere queste curve, non descriveremo solo i singoli segmenti curvilinei che le compongono (come abbiamo fatto nella trattazione precedente), ma descriveremo la curva nel suo insieme, considerando tutti i suoi segmenti contemporaneamente.
Le B-spline cubiche approssimano una serie di m+1
punti di controllo P0, P1,
Ö e Pm, dove 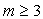
Per ogni i 4, vi è un punto di giunzione, chiamato knot, tra i segmenti Qiñ1 e Qi, in corrispondenza del valore ti del parametro, chiamato knot-value. Anche il punto iniziale t3 e quello finale tm+1 sono detti knot, così che il numero totale di knot è pari a m-1.
Le B-spline si dividono in B-spline uniformi e B-spline non uniformi. Nelle prime gli knot sono ugualmente spaziati rispetto al parametro t. Senza perdere di generalità possiamo fare líipotesi che t3 = 0, e che gli intervalli tra gli knot siano unitari: ti+1 ñ ti = 1. Le B-spline non uniformi permettono invece di avere intervalli differenti tra gli knot.
Ciascuno degli mñ2 segmenti curvilinei di una B-spline è definito da quattro degli m+1 punti di controllo. In particolare, il tratto Qi è definito dai punti Piñ3 , Piñ2, Piñ1 e Pi. La matrice geometrica della B-spline relativa al segmento curvilineo Qi, GBSi, è dunque data da
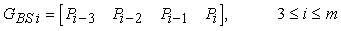
Il primo tratto, Q3, è definito dai punti P0, P1, P2 e P3, ed il parametro t varia tra t3 = 0 e t4 = 1; Q4 è definito dai punti P1, P2, P3 e P4 e t è compreso tra i valori t4 = 1 e t5 = 2; líultimo tratto, Qm, è definito dai punti Pmñ3 , Pmñ2 , Pmñ1 e Pm, e il parametro t è compreso tra i valori tm = m ñ 3 e tm+1 = m ñ 2. In generale, il tratto curvilineo Qi inizia in prossimità del punto Piñ2 e termina in prossimità del punto Piñ1. Le funzioni blending relative alle B-spline risultano ovunque non negative e la loro somma risulta pari a 1, così che il segmento Qi è confinato nel convex hull dei suoi quattro punti di controllo.
In analogia ai segmenti curvilinei, che sono definiti tramite quattro punti di controllo, ogni punto di controllo (ad eccezione del primo e dellíultimo della sequenza P0, P1, Ö e Pm) influenza esattamente quattro segmenti curvilinei. Muovendo un punto di controllo in una certa direzione, i quattro segmenti che esso influenza vengono mossi nella stessa direzione, mentre tale movimento non influenza affatto gli altri segmenti curvilinei. Per questo motivo si parla di controllo locale.
Indicando con Ti il vettore colonna [(t ñ ti)3 (t ñ ti)2 (t ñ ti) 1]T, si ottiene la seguente formulazione per líi-esimo tratto curvilineo
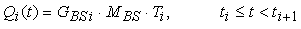
Applicando questa equazione in corrispondenza di tutti i valori di i compresi tra 3 ed m, si genera dunque líintera curva.
La matrice base B-spline, MBS, mette in relazione i vincoli geometrici espressi nella matrice GBS con le funzioni blending e i coefficienti polinomiali. Si può dimostrare che tale matrice risulta pari a
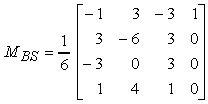
Le funzioni blending BBS sono definite dal prodotto MBS _ Ti. Si osservi che le funzioni blending relative a ciascun segmento curvilineo sono esattamente uguali poiché, per ogni i, i valori di t ñ ti variano tra 0 (per t = ti) e 1 (per t ñ ti+1). Sostituendo t ñ ti con t, e líintervallo [t, ti+1] con [0, 1], abbiamo
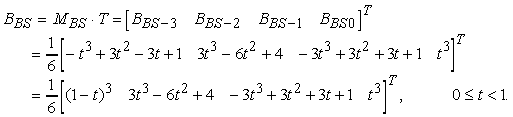
Sviluppando líequazione, e sostituendo t ñ ti con t, si ottiene quindi
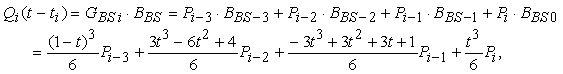
dove 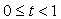
Non è difficile dimostrare che Qi e Qi+1 hanno continuità di classe C0, C1 e C2 nei punti di giunzione. Questa maggiore continuità ha però un costo che è dato dal minore controllo sulla direzione della curva. Possiamo forzare la curva facendo in modo che interpoli alcuni punti duplicando i punti di controllo; questo può risultare utile sia per gli estremi che per i punti intermedi sulla curva. Ad esempio, se Piñ2 = Piñ1, la curva risulta più vicino a questo punto poiché il tratto Qi è definito da tre soli punti diversi, ed il punto Piñ2 = Piñ1 è pesato due volte nellíequazione (10.31), una volta dalla funzione blending BBSñ2 e una volta dalla funzione BBSñ1. Se un punto di controllo è utilizzato tre volte, ad esempio se Piñ2 = Piñ1 = Pi, allora líequazione (10.31) diventa
Qi(t) = Piñ3 _ BBSñ3 + Pi _ (BBSñ2 + BBSñ1 + BBS0). (10.32)
In questo caso, Qi è chiaramente un segmento rettilineo. Inoltre il punto Piñ2 è interpolato dalla linea in corrispondenza del valore t = 1, dove i tre pesi applicati a Pi hanno somma pari a 1; tuttavia Piñ3 non è in generale interpolato a t = 0. Un altro modo di pensare a questo comportamento è che il convex hull relativo a Qi è definito da due soli punti distinti, quindi Qi deve essere un segmento rettilineo.
Le B-spline non uniformi permettono di interpolare in modo più naturale sia gli estremi che i punti intermedi sulla curva.
Le B-spline non uniformi si differenziano da quelle uniformi per il fatto che líintervallo parametrico tra gli knot non è necessariamente uniforme. Di conseguenza, le funzioni blending non sono più uguali per tutti gli intervalli, ma cambiano da segmento curvilineo a segmento.
Queste curve hanno diversi vantaggi rispetto a quelle uniformi. Per prima cosa la continuità in certi punti di giunzione, opportunamente selezionati, può essere ridotta da C2 a C1 a C0 a nessuna continuità. Se la continuità è ridotta alla classe C0, allora la curva interpola un punto di controllo, senza gli effetti indesiderati introdotti dalle B-spline uniformi, dove i segmenti curvilinei adiacenti al punto di controllo interpolato diventano rettilinei. Inoltre, il punto iniziale e quello finale risultano facilmente interpolabili, senza dovere introdurre segmenti lineari.
Anche in questo caso abbiamo una curva continua a tratti, composta da curve polinomiali cubiche, che approssima i punti di controllo P0, P1, Ö e Pm. La sequenza degli knot-value è una sequenza non decrescente dei valori del parametro t corrispondenti ai punti di giunzione, da t0 a tm+4. Dunque ci sono quattro knot in più rispetto ai punti di controllo.
Poiché il numero minimo di punti di controllo è quattro, la più piccola sequenza di knot-value è composta da otto valori, e la curva è definita sullíintervallo parametrico da t3 a t 4.
La sola restrizione sulla sequenza è che essa sia non decrescente, cosa che permette di avere knot-value successivi anche uguali. Quando ciò si verifica, il valore parametrico è chiamato knot-multiplo, e il numero di valore identici è detto molteplicità dello knot.
Il segmento curvilineo Qi è definito dai punti di controllo Piñ3, Piñ2, Piñ1 e Pi e dalle funzioni blending Bi3,4(t), Bi2,4(t), Bi1,4(t), Bi,4(t) attraverso la somma pesata
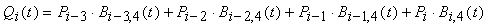
dove 3 i m e
ti t < ti+1.
La curva non è definita al di fuori dellíintervallo
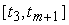
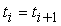
Le funzioni blending dipendono dagli intervalli tra gli knot e sono definite ricorsivamente in termini delle funzioni blending di ordine inferiore. Bi,j(t) è la funzione blending di j-esimo ordine, relativa al punto di controllo Pi. Poiché stiamo lavorando con B-spline del quarto ordine (cioè di terzo grado, o cubiche), la definizione ricorsiva si arresta a Bi,4(t). La ricorrenza per le B-spline cubiche è dunque data da
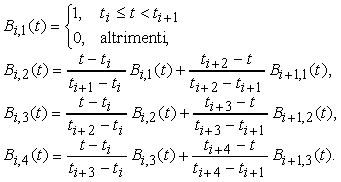
Si può dimostrare che le funzioni blending risultano ovunque non negative, e che la loro somma è pari a 1. Dunque, i segmenti curvilinei delle B-spline non uniformi giacciono allíinterno dellíinviluppo convesso (convex hull) definito dai loro quattro punti di controllo. Per gli knot di molteplicità maggiore di uno, il denominatore può risultare uguale a zero, e in questo caso si assume che la divisione per zero dia il valore zero.
Líaumento della molteplicità degli knot produce due effetti. Per prima cosa, la spline, valutata ad ogni knot-value ti conosciuto, fornisce immediatamente un punto interno al convex hull dei punti Piñ3, Piñ2 e Piñ1. Se ti e ti+1 sono uguali, essi devono trovarsi nel convex hull di Piñ3, Piñ2 e Piñ1, e nel convex hull di Piñ2, Piñ1 e Pi. Dunque, essi devono giacere sul segmento lineare tra Piñ2 e Piñ1. In modo del tutto analogo, se ti = ti+1 = ti+2, allora questo knot deve trovarsi nel punto Piñ1. Se ancora ti = ti+1 = ti+2 = ti+3, allora lo knot deve trovarsi sia in corrispondenza del punto Piñ1 che del punto Pi, quindi la curva si spezza. In secondo luogo, gli knot multipli riducono la continuità parametrica: da C2 a C1 per knot di molteplicità 2; da C1 a C0 per knot di molteplicità 3; e da C0a nessuna continuità per knot di molteplicità 4.