| Mesh Decimation |
![]() Lo scopo
del processo di decimazione Ŕ quello di ridurre la complessitÓ di una mesh
in termini di numero di facce e di vertici. Il processo qui proposto Ŕ
iterativo; ad ogni passo viene scelto un vertice da rimuovere, i triangoli in esso
incidenti sono rimossi e il "buco" che essi creano Ŕ "coperto" con un
nuovo insieme di triangoli. Il processo continua soltanto se l’errore commesso,
togliendo il vertice, Ŕ minore di una soglia fissata. Il numero di passi dipende, quindi,
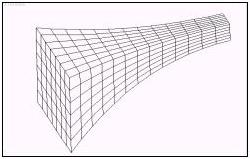
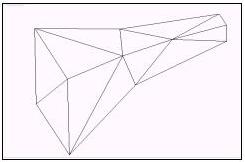
dal tasso di riduzione che si vuole raggiungere. In figura Ŕ rappresentato un
parallelepipedo "rastremato" costituito da 282 vertici e 560 facce.
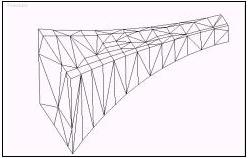
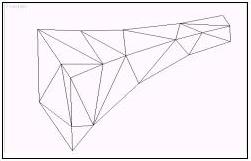
Nelle figure successive lo stesso oggetto dopo la riduzione rispettivamente del 70%, 90% e
95% dei suoi vertici.
Lo scopo
del processo di decimazione Ŕ quello di ridurre la complessitÓ di una mesh
in termini di numero di facce e di vertici. Il processo qui proposto Ŕ
iterativo; ad ogni passo viene scelto un vertice da rimuovere, i triangoli in esso
incidenti sono rimossi e il "buco" che essi creano Ŕ "coperto" con un
nuovo insieme di triangoli. Il processo continua soltanto se l’errore commesso,
togliendo il vertice, Ŕ minore di una soglia fissata. Il numero di passi dipende, quindi,
dal tasso di riduzione che si vuole raggiungere. In figura Ŕ rappresentato un
parallelepipedo "rastremato" costituito da 282 vertici e 560 facce.
Nelle figure successive lo stesso oggetto dopo la riduzione rispettivamente del 70%, 90% e
95% dei suoi vertici.
![]() Sia V
l’insieme dei vertici della mesh e F l’insieme delle facce
triangolari di cui Ŕ formata. Il processo di decimazione determina, ad generico passo i,
un nuovo insieme di vertici V(i) e un nuovo insieme di facce F(i):
Sia V
l’insieme dei vertici della mesh e F l’insieme delle facce
triangolari di cui Ŕ formata. Il processo di decimazione determina, ad generico passo i,
un nuovo insieme di vertici V(i) e un nuovo insieme di facce F(i):
M(V(0),F(0))« M(V(1),F(1)) « M(V(2),F(2))« M(V(3),F(3)) « ……
Dove :
V(0) ╩ V(1) ╩ V(2)╩ V(3)╩ ……
Siano S(i) l’insieme della facce triangolari dell’area da triangolare al passo i e T ottima(i) l’insieme delle nuove facce (chiamata triangolazione ottima). Allora vale:
F(i) = F(i-1) \ S(i) ╚ T ottima(i)
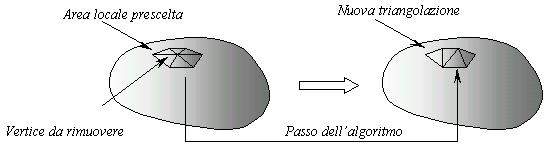
![]() In
figura Ŕ rappresentato un passo di semplificazione consistente nell’eliminazione di
un vertice e dei triangoli in esso adiacenti e la relativa ritriangolazione del
"buco" (chiamato poligono 3D). Una parte fondamentale del processo di
decimazione Ŕ l’algoritmo che costruisce la nuova triangolazione; una sua
implementazione efficiente determina l’efficienza dell’intero processo.
In
figura Ŕ rappresentato un passo di semplificazione consistente nell’eliminazione di
un vertice e dei triangoli in esso adiacenti e la relativa ritriangolazione del
"buco" (chiamato poligono 3D). Una parte fondamentale del processo di
decimazione Ŕ l’algoritmo che costruisce la nuova triangolazione; una sua
implementazione efficiente determina l’efficienza dell’intero processo.